Конспект урока «Векторы в пространстве», 1 курс
- Просмотр содержимого документа «Конспект урока «Векторы в пространстве», 1 курс»
- Конспект урока по математике на тему «Понятие вектора» 1 курс СПО
- «Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
- Вектор: определение и основные понятия
- Определение вектора
- Обозначение вектора
- Длина вектора
- Нулевой вектор
- Коллинеарные вектора
- Сонаправленные вектора
- Противоположно направленные вектора
- Компланарные вектора
- Равные вектора
- Единичный вектор
- 🌟 Видео
Просмотр содержимого документа
«Конспект урока «Векторы в пространстве», 1 курс»
ОГБПОУ Фурмановский технический колледж, преподаватель Цветкова Елена Ивановна
Разработка урока на тему:
Векторы в пространстве. Действия с векторами. Разложение вектора на составляющие.
Ввести определения вектора в пространстве, равенства векторов. Рассмотреть правила действия над векторов, правило сложения нескольких векторов в пространстве.
Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность.
Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.
1. Орг. момент. Настрой на урок.
2. Мотивация урока.
Поразмышляйте над содержанием пословицы «Плохо, когда сила живет без ума, да нехорошо, когда и ум без силы». То есть, если есть сила, то надо знать, куда ее направить. От этого зависит, будет ли пружина сжиматься или растягиваться, полетит ли мяч в ворота противника или в собственные и многое другое. Вы уже, конечно, догадались, что сегодня речь пойдет о векторах, причем о векторах в пространстве. Геометрия – одна из самых интереснейших наук, которая изучает много важных и интересных тем. Одна из них – это “Векторы”. С понятием “Вектор” вы уже знакомы, но вы знакомы с векторами на плоскости, а сегодня мы пополним свои знания о векторах и рассмотрим “Векторы в пространстве”
3. Актуализация опорных знаний. Проверка д/з.
Решить № 8, стр. 68.
Что называется вектором на плоскости?
Приведите пример векторных величин.
Что такое абсолютная величина вектора; направление вектора?
Какие векторы называются равными?
Сформулируйте правила сложения двух векторов на плоскости.
Какой вектор называют разницей двух векторов?
4. Объяснение нового материала сопровождается презентацией:
Впервые понятие вектора появилось в работах немецкого математика 19 века Г. Грассмана и ирландского математика У. Гамильтона; затем его использовали в своих открытиях многие ученые. Современная символика для обозначения вектора была введена в 1853 году французским математиком О. Коши. Применение векторов играет важнейшую роль в современной математике, химии, биологии, экономике и в других науках.
Векторы на плоскости были изучены в 9 классе в разделе “Планиметрия”. Сегодня на уроке рассмотрим векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия сходны с определением вектора на плоскости и связанными с ним понятиями.
Раз мы уже знакомы с векторами на плоскости, то нам будет не трудно говорить о векторах в пространстве. Результатом нашей работы станет опорный конспект.
Что такое вектор? Как построить вектор? Как обозначаются вектора?
Обратите внимание: что над буквенным обозначением вектора ставится стрелка или черта- в разной литературе по- разному. Так, например, в учебнике физики — стрелка, а в учебнике геометрии — черта.
Вектором называется направленный отрезок.
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой приложения);
2 )направлением;
3) длиной («модулем вектора»).
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается 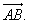
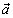

От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления. Обозначается: 
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина вектора 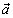

Два вектора называются равными, если они совмещаются параллельным переносом.
АВСD — параллелограмм,
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если векторы 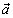
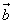
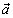
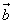
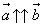
Если векторы 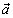

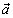

Обозначаются 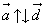
Свойство коллинеарных векторов
Если векторы 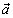
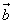
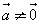
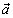
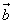
Правило треугольника. Каковы бы ни были точки А, В, С, имеет место векторное равенство:
Правило параллелограмма. Если векторы 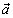
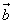
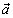
Координаты вектора. Числа x, y и z называются координатами вектора в данном базисе. В этом случае пишут:
Действия над векторами, заданными своими координатами
При сложении векторов их соответстветственные координаты
складываются.
При вычитании векторов их соответстветственные координаты
вычитаются.
При умножении вектора на число все его координаты умножаются на это число.
5. Первичное закрепление нового материала. Выполнение устных упражнений
Дан прямоугольный параллелепипед. Назовите сонаправленные векторы; противоположно направленные векторы.
Запишите координаты вектора АО, если А(6;-2;4), О – начало координат?
Найти координаты вектора АВ, если А(3; 4; -1) и В( -2; 0; 4)
Дано: АВ= СD, где А ( 1;0;1),В ( -1; 1;2), С (0;2;-1). Найти: D( х ,у,z)
Коллективное решение задач:
В пространстве даны точки А, В, С, D. Найдите вектор с началом и концом в этих точках, который равен: а) ВС+СА+АD; б) АВ+ВD+BA-CD.
Найдите координаты конца вектора АВ(1;-3;7), если А(2;5;-1).
У какого из приведенных векторов самая большая длина:
Решить № 3, 5, 6, 7 стр.73
6. Зарядка для глаз.
Решение задач П-23,24. Устно 1-3,5,10,11. П-23, 1-3,
Работа в группах остальные номера.
Итоги урока. Рефлексия.
Что называют вектором?
Выполняется ли правило параллелограмма и правило треугольника в случае сложения векторов в пространстве?
Сформулируйте правило параллелепипеда для сложения векторов в пространстве?
Какие векторы называются равными?
Какие векторы называются сонаправленными в пространстве; противоположно направленными в пространстве?
Д/з: учить пп. 23, 24. Решить : 14,15. Сообщение «Применение векторов».
Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать

Конспект урока по математике на тему «Понятие вектора» 1 курс СПО
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Тема урока: «Понятие вектора в пространстве»
Тип урока: Изучение нового материала
Образовательные: ввести определение вектора в пространстве и связанные с ним понятия; дать определение равенства векторов; отработать навыки нахождения равных, сонаправленных, противоположно направленных векторов; научить решать задачи по данной теме.
Развивающие: развивать стремление к достижению поставленной цели; совершенствовать пространственное воображение и мышление учащихся; развивать навыки диалоговой культуры.
Воспитательные: воспитать математическую культуру, грамотность; формировать активность, внимательность, наблюдательность; воспитание интереса к предмету и потребности в приобретении знаний.
Методы: беседа, лекция
Оборудование: учебники, тетради, меловая доска
I. Организационный момент
Геометрия — увлекательная наука, где есть важные и интересные темы.
Итак, запишите в тетрадях тему урока «Понятие вектора. Равенство векторов»
Сегодня на уроке мы познакомимся
— с понятием вектора в пространстве, с равными векторами в пространстве
— будем отрабатывать навыки нахождения равных, сонаправленных, противоположно направленных векторов
— узнаем, какую роль играют векторы в различных областях науки.
II. Актуализация опорных знаний.
1. Анализ контрольной работы. Подвести итоги контрольной работы. Анализ наиболее часто встречающихся ошибок.
2. Подготовка к восприятию нового материала.
Понятие вектора является одним из наиболее основных в математике, объединяющим такие ее разделы, как геометрия, алгебра, математический анализ. Оно имеет большое прикладное значение, так как многие физические величины (сила, скорость, и другие) характеризуются не только величиной, но и направлением, то есть являются векторными величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин (векторы напряженности электрического поля, вектор магнитной индукции).
Ⅲ. Изучение нового материала
Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.
Определение. Длиной ненулевого вектора 



Определение. Коллинеарные векторы – это ненулевые векторы, которые лежат на одной прямой или на параллельных прямых.
Коллинеарные векторы делятся на сонаправленные и противоположно направленные.
Учащиеся называют по чертежу векторы, сонаправленные с вектором 
Нулевой вектор считается сонаправленным с любым вектором.
Определение. Векторы называются равными, если они сонаправлены и их длины равны.
IV. Закрепление изученного материала.
Решение задачи № 320.
Найдите длину векторов: 






Вспомнить свойства граней и диагоналей параллелепипеда. По рисунку учащиеся называют все пары:
Найдите длины векторов


Назовите все векторы, противоположные вектору 
Ответ:
Назовите все векторы, противоположные вектору 
Ответ:
Назовите все векторы, равные вектору
Ответ:
V. Самостоятельная работа (обучающая)
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Вектор: определение и основные понятия
Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Определение вектора
 |
| рис. 1 |
Видео:Математика это не ИсламСкачать

Обозначение вектора
Вектор началом которого есть точка А, а концом — точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a .
Видео:СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Длина вектора
Для обозначения длины вектора используются две вертикальные линии слева и справа | AB |.
Видео:Вектора. Что нужно знать про вектор, когда идешь на первый курс.Скачать

Нулевой вектор
Нулевой вектор обычно обозначается как 0 .
Длина нулевого вектора равна нулю.
Видео:Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать

Коллинеарные вектора
 |
| рис. 2 |
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Сонаправленные вектора
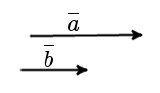 |
| рис. 3 |
Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Противоположно направленные вектора
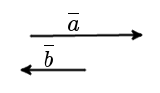 |
| рис. 4 |
Видео:Высшая математика. Линейные пространства. Векторы. БазисСкачать

Компланарные вектора
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Равные вектора
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b , если a ↑↑ b и | a | = | b |.
Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

Единичный вектор
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
🌟 Видео
§1 ВекторыСкачать

Координаты вектора. 9 класс.Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать