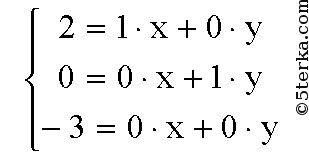Этот онлайн калькулятор позволит вам очень просто проверить являются ли три вектора компланарными.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на проверку компланарности трех векторов и закрепить пройденый материал.
- Калькулятор для проверки компланарности векторов
- Ввод данных в калькулятор для проверки компланарности векторов
- Дополнительные возможности калькулятора для проверки компланарности векторов
- Теория. Компланарность векторов
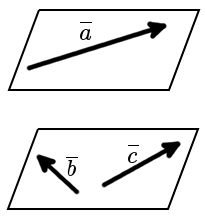
- 415. Компланарны ли векторы: а) а , i и j; б) b, i и j; в) с, i и k; г) d , е и f; д) m , n и р ; е) q, F и s ?
- Компланарные векторы и условие компланарности
- Определение компланарных векторов
- Условия компланарности векторов
- 🌟 Видео
Видео:10 класс, 43 урок, Компланарные векторыСкачать

Калькулятор для проверки компланарности векторов
Ввод данных в калькулятор для проверки компланарности векторов
Из имеющихся у вас данных введите значения трех векторов которые будут проверяться на компланарность. После нажатия кнопки «Проверить компланарны ли три вектора» вы получите детальное решение задачи.
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для проверки компланарности векторов
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Видео:43. Компланарные векторыСкачать

Теория. Компланарность векторов
Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

415. Компланарны ли векторы: а) а , i и j; б) b, i и j; в) с, i и k; г) d , е и f; д) m , n и р ; е) q, F и s ?
Р е ш е н и е. г) Векторы d и e не коллинеарны, так как координаты одного не пропорциональны координатам другого. Если вектор f можно разложить по векторам d и e , то векторы d , е и f компланарны. Если же вектор f нельзя разложить по векторам d и e , то векторы d , е и f не компланарны (в противном случае вектор f можно было бы разложить по векторам d и e ). Таким образом, для решения задачи нужно установить, можно ли вектор f разложить по векторам d и e , т. е. существуют ли числа x и y такие, что
Записывая это равенство в координатах, получим
Если эта система уравнений имеет решение относительно х и у, то вектор f можно разложить по векторам d и e , а если не имеет решения, то вектор f нельзя разложить по векторам d и e . В данном случае система имеет решение: х = 1, у = — 2.
Поэтому вектор f можно разложить по векторам d и e , и,
значит, векторы d , e и f компланарны.
являются компланарными, т. к., записав равенство
через координаты, получим
Вектор a можно разложить по векторам
Значит векторы a , i и j компланарны.
б) Запишем равенство
Система не имеет решений, следовательно, b , i и j не компланарны.
в) Запишем равенство
не коллинеарны, т.к. координаты век
тора d не пропорциональны координатам вектора e . Если вектор
можно разложить по векторам d и e , то это значит, что векторы d , e и f компланарны. В противном случае векторы d , e и f не компланарны.
в координатах, получим
Система имеет решение: х=1, у=-2. Поэтому вектор f можно разложить по векторам d и e , и, следовательно, векторы d , e и f компланарны.
д) Запишем равенство
Система не имеет решений. Поэтому векторы m , n и p не компланарны.
е) Запишем равенство
Система не имеет решений. Поэтому векторы

задача №415
к главе «Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора.».
Видео:Задача 5. Компланарны ли векторы a, b, c.Скачать

Компланарные векторы и условие компланарности
В данной статье мы рассмотрим такие темы, как:
- определение компланарных векторов;
- условия компланарности векторов;
- примеры задач на компланарность векторов.
Видео:КОМПЛАНАРНЫЕ ВЕКТОРЫ | геометрия 11 класс АтанасянСкачать

Определение компланарных векторов
Компланарные векторы — это векторы, которые параллельны одной плоскости или лежат на одной плоскости.
Два любых вектора всегда компланарны, поскольку всегда можно найти плоскости параллельные 2-м произвольным векторам.
Видео:Компланарные векторы. Видеоурок по геометрии 10 классСкачать

Условия компланарности векторов
- Для 3-х векторов выполняется условие: если смешанное произведение 3-х векторов равно нулю, то эти три вектора компланарны.
- Для 3-х векторов выполняется условие: если три вектора линейно зависимы, то они компланарны.
- Для n-векторов выполняется условие: если среди векторов не более 2-х линейно независимых векторов, то они компланарны.
Примеры решения задач на компланарность векторов
Исследуем на компланарность векторы
a ¯ = ( 1 ; 2 ; 3 ) , b = ( 1 ; 1 ; 1 ) и c ¯ = ( 1 ; 2 ; 1 )
Как решить?
Векторы будут являться компланарными, если их смешанное произведение равно нулю, поэтому вычисляем смешанное произведение заданных векторов. Для этого составляем определитель, по строкам которого записываются координаты векторов-сомножителей:
( a ¯ , b ¯ , c ¯ ) = 1 2 3 1 1 1 1 2 1 = = 1 × 1 × 1 + 1 × 2 × 3 + 2 × 1 × 1 — 1 × 1 × 3 — 2 × 1 × 1 — 1 × 2 × 1 = 2 ≠ 0
Отсюда следует, что смешанное произведение не равняется нулю, поэтому векторы не являются компланарными.
Ответ: векторы не являются компланарными.
Докажем, что три вектора
a ¯ = ( 1 ; — 1 ; 2 ) , b = ( 0 ; 1 ; — 1 ) и c ¯ = ( 2 ; — 2 ; 4 ) компланарны.
Как решить?
Находим смешанное произведение данных векторов:
( a ¯ , b ¯ , c ¯ ) = 1 — 1 2 0 1 — 1 2 — 2 4 = = 1 × 1 × 4 + 0 × ( — 2 ) × 2 + ( — 1 ) × ( — 1 ) × × 2 — 2 × 1 × 2 — ( — 2 ) × ( — 1 ) × 1 — 0 × ( — 1 )
Из данного примера видно, что смешанное произведение равняется нулю.
Ответ: векторы являются компланарными.
Проверим, компланарны ли векторы
Как решить?
Необходимо найти количество линейно независимых векторов: записываем значения векторов в матрицу и выполняем элементарные преобразования:
1 1 1 1 2 0 0 — 1 1 3 3 3
Из 2-ой строки вычитаем 1-ю, из 4-ой вычитаем 1-ю, умноженную на 3:
1 1 1 1 — 1 2 — 1 0 — 1 0 — 1 1 3 — 3 3 — 3 3 — 3
1 1 1 0 1 — 1 0 — 1 1 0 0 0
К 3-ей строке прибавляем 2-ю:
1 1 1 0 1 — 1 0 + 0 — 1 + 1 1 + ( — 1 ) 3 — 3 3 — 3 3 — 3
1 1 1 0 1 — 1 0 0 0 0 0 0
Поскольку в матрице только две ненулевые строки, делаем вывод, что среди них всего два линейно независимых вектора.
Ответ: векторы являются компланарными, поскольку среди них всего два линейно независимых вектора.
🌟 Видео
ГЕОМЕТРИЯ 11 класс: Компланарные векторыСкачать

Компланарность векторовСкачать

Компланарные векторы. Видеоурок 18. Геометрия 10 классСкачать

Компланарные векторыСкачать

Коллинеарность векторовСкачать

Геометрия 10 класс (Урок№18 - Компланарные векторы. Векторный метод решения задач.)Скачать

10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Геометрия. 10 класс. Коллинеарность и компланарность векторов /13.04.2021/Скачать

№355. Дан параллелепипед ABCDA1B1C1D1. Какие из следующих трех векторов компланарныСкачать

Коллинеарные векторы.Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Решение, компланарны ли следующие векторы: а) а=(7, 3, 4), b=(−1, −2, −1), с=(4, 2, 4) пример 10Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать