Коммутативность ассоциативность дистрибутивность векторов

Прежде чем приступить к тематике статьи, напомним основные понятия.

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Сложение двух векторов

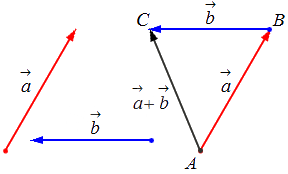
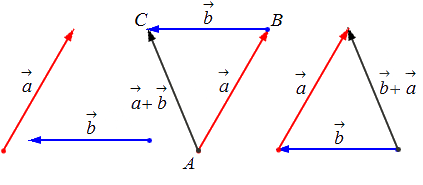
Исходные данные: векторы a → и b → . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор A B → , равный вектору а → ; из полученной точки undefined – вектор В С → , равный вектору b → . Соединив точки undefined и C , получаем отрезок (вектор) А С → , который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

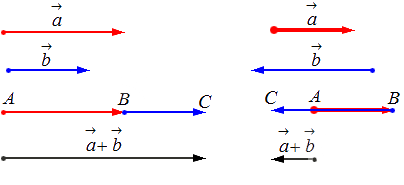
— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

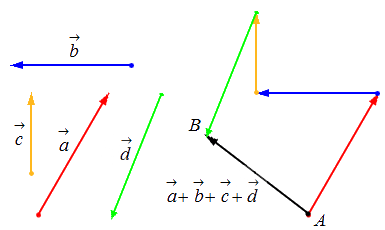
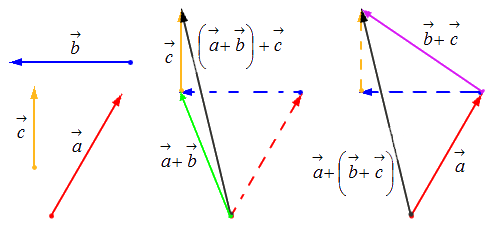
Исходные данные: векторы a → , b → , c → , d → . Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a → ; затем от конца полученного вектора откладывается вектор, равный вектору b → ; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B , а полученный отрезок (вектор) A B → – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a → и b → есть сумма векторов a → и — b → .

Умножение вектора на число

Чтобы произвести действие умножения вектора на некое число k , необходимо учитывать следующие правила:
— если k > 1 , то это число приведет к растяжению вектора в k раз;
— если 0 k 1 , то это число приведет к сжатию вектора в 1 k раз;
— если k 0 , то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k = 1 , то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

Исходные данные:
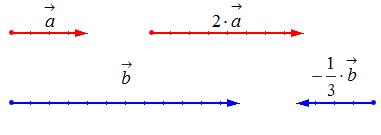
1) вектор a → и число k = 2 ;
2) вектор b → и число k = — 1 3 .

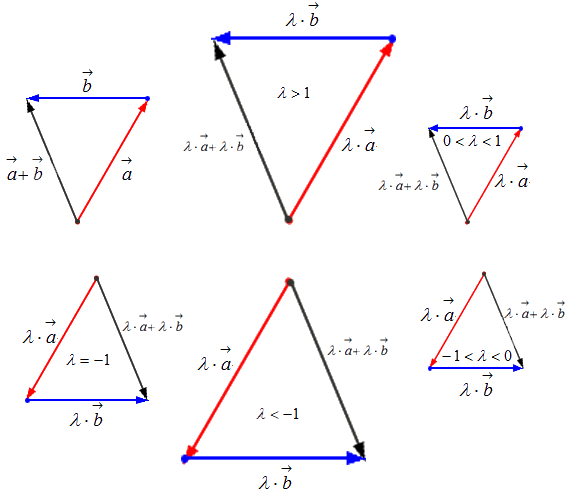
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a → , b → , c → и произвольные действительные числа λ и μ .

1. Свойство коммутативности: a ⇀ + b → = b → + a → .
   
2. Свойство ассоциативности: ( a → + b → ) + c → = a → + ( b → + c → ) .
   
3. Свойство использования нейтрального элемента по сложению (нулевой вектор 0 → ⃗). Это очевидное свойство: a → + 0 → = a →
4. Свойство использования нейтрального элемента по умножению (число, равное единице): 1 · a → = a → . Это очевидное свойство, не предполагающее никаких геометрических преобразований.
5. Любой ненулевой вектор a → имеет противоположный вектор — a → и верным является равенство: a → + ( — a → ) = 0 → . Указанное свойство — очевидное.
6. Сочетательное свойство операции умножения: ( λ · µ ) · a → = λ · ( µ · a → ) . Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
7. Первое распределительное свойство (очевидно): ( λ + µ ) · a → = λ · a → + µ · a → .
8. Второе распределительное свойство: λ · ( a → + b → ) = λ · a → + λ · b → .
   Геометрически это свойство определяется подобием треугольников:
   

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Задача: упростить выражение a → — 2 · ( b → + 3 · a → )
Решение
— используя второе распределительное свойство, получим: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · ( 3 · a → )
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a → — 2 · b → — 2 · ( 3 · a → ) = a → — 2 · b → — ( 2 · 3 ) · a → = a → — 2 · b → — 6 · a →
— используя свойство коммутативности, меняем местами слагаемые: a → — 2 · b → — 6 · a → = a → — 6 · a → — 2 · b →
— затем по первому распределительному свойству получаем: a → — 6 · a → — 2 · b → = ( 1 — 6 ) · a → — 2 · b → = — 5 · a → — 2 · b → Краткая запись решения будет выглядеть так: a → — 2 · ( b → + 3 · a → ) = a → — 2 · b → — 2 · 3 · a → = 5 · a → — 2 · b →
Ответ: a → — 2 · ( b → + 3 · a → ) = — 5 · a → — 2 · b →

Коммутативность ассоциативность дистрибутивность векторов

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии

Аналитическая геометрия
Bodrenko.com
Bodrenko.org

1.2 Операции над векторами.

Сложение векторов. Сумма векторов а и b определяется следующим образом. Отложим вектор а от произвольной точки А, пусть В — конец этого вектора, т.е. а = . Затем отложим вектор b от точки В, пусть b = . Суммойа + bвекторова и b называется вектор, порожденный направленным отрезком (рис.1)
.
Это правило сложения векторов называется правилом треугольника. Очевидно, что этот же вектор а + b для неколлиниарных векторов а и b может быть получен (рис.2) как диоганаль параллелограмма, построенного на векторах а и b. Это правило сложения векторов называется правилом параллелограмма.

Теорема 2.1. Операция сложения векторов обладает следующими свойствами:
1)а + b = b + а, ∀ а, b (свойство коммутативности);
2) (а + b) + с = а + (b + с), ∀ а, b, с (свойство ассоциативности);
3) существует такой вектор 0, называемый нулевым вектором, что
а + 0 = 0 + а = а, ∀ а (свойство существования нейтрального элемента);
4) для любого вектора а существует такой вектор — а (называемый противоположным к вектору a), что а + (- а) = 0 (свойство существования симметричного элемента).

Доказательство. Коммутативность и ассоциативность сложения в случае неколлиниарных векторов а, b и с проверяется непосредственным построением (рис.3) векторов левой и правой частей соответствующих равенств.

Свойства 3 и 4 очевидны: нулевым вектором 0 будет класс эквивалентности нулевых направленных отрезков, противоположным к вектору а = будет вектор
-а = .Теорема доказана.

Разностьювекторов b и а называется вектор x такой, что а + x = b. Обозначение: b — а.

Теорема 2.2. Для любых векторов а и b существует, и притом единственная, разность b — а.

Доказательство. В качестве разности b — а можно взять вектор b + (- а), так как а + (b + (- а)) = а + ((-а) + b) = (а + (-а)) + b = 0 + b = b. Эта разность единственная, так как если с − еще одна разность, то с = с + 0 = (с + а) + (-а) = b + (-а).
Теорема доказана.

Замечание. Правило параллелограмма сложения неколлиниарных векторов а и b позволяет построить и разность b — а как другую диагональ параллелограмма (рис.4).

Умножение вектора на число. Произведением вектора а на вещественное число α называется вектор b, удовлетворяющий следующим условиям:
1) |b| = |α|•|а| и, в случае b ≠ 0,
2) b ↑↑ а, если α > 0, и b ↑↓ а, если α

Свойства операций (коммутативность, ассоциативность, дистибутивность)

Оговорюсь сразу: под значками «○», «⊕» и «⊗» не прячутся какие-то неизвестные вам математические операции. Как под X мы «прячем» неизвестное значение, так и тут, под этими значками прячется какая-то операция.

Коммутативность

Операция обладает свойством коммутативности, если для любых a и b выполняется равенство:

Например, сложение и умножение обладают коммутативностью:

А вот возведение в степень — не обладает:

Ассоциативность

Операция обладает свойством ассоциативности, если для любых a и b выполняется равенство:

Сложение и умножение ассоциативны:

Возведение в степень не обладает и свойством ассоциативности:

Дистрибутивность

Говорят, что бинарная операция «⊗» является дистрибутивной относительно бинарной операции «⊕», если для любых a, b и c они удовлетворяют следующим двум тождествам:

Дистрибутивность слева:

Дистрибутивность справа:

Например, умножение дистрибутивно относительно сложения:

Но сложение не дистрибутивно относительно умножения: