Коллинеарные вектора в трапеции (4 видео)

Коллинеарные векторы

В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.

Содержание

Условия коллинеарности векторов
Примеры задач
Условие коллинеарности векторов
Координатная форма условия коллинеарности векторов
Разработка урока по теме «Применение векторов к решению задач. Средняя линия трапеции».
«Управление общеобразовательной организацией: новые тенденции и современные технологии»
📸 Видео

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Условия коллинеарности векторов

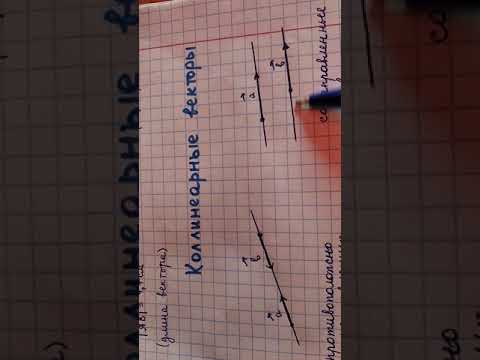
Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.

Два вектора коллинеарны, если выполняется одно из условий ниже:

1. Существует такое число n, при котором .

2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.

3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).

Видео:Коллинеарность векторовСкачать

Примеры задач

Задание 1
Даны векторы , и . Определим, есть ли среди них коллинеарные.

Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.

Следовательно, коллинеарными являются только векторы a и c .

Задание 2
Выясним, при каком значении n векторы и коллинеарны.

Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Условие коллинеарности векторов

В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.

Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.

Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.

Согласно схемам операций над векторами умножение вектора на некоторое заданное число приводит к соответствующему сжатию или растяжению вектора при сохранении или смене направления. Тогда вектор b → = λ · a → коллинеарен вектору a → , где λ – некоторое действительное число. Справедливым будет и обратное утверждение: если вектор b → коллинеарен вектору a → , его можно представить в виде λ · a → . Это является необходимым и достаточным условием коллинеарности двух ненулевых векторов.

Для коллинеарности двух векторов необходимо и достаточно, чтобы они были связаны равенствами: b → = λ · a → или a → = μ · b → , μ ∈ R

Видео:№747. Выпишите пары коллинеарных векторов, которые определяются сторонами: а) параллелограмма MNPQСкачать

Координатная форма условия коллинеарности векторов

Исходные данные: вектор a → задан в некоторой прямоугольной системе координат на плоскости и имеет координаты ( a x , a y ) , тогда, согласно полученному выше условию, вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y ) .

По аналогии: если вектор a → задан в трехмерном пространстве, то он будет представлен в виде координат a = ( a x , a y , a z ) , а вектор b → = λ · a → имеет координаты ( λ · a x , λ · a y , λ · a z ) . Из полученных утверждений следуют условия коллинеарности двух векторов в координатном толковании.

Для коллинеарности двух ненулевых векторов на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y или a x = μ · b x a y = μ · b y
Для коллинеарности двух ненулевых векторов в пространстве необходимо и достаточно, чтобы их координаты были связаны соотношениями: b x = λ · a x b y = λ · a y b z = λ · a z или a x = μ · b x a y = μ · b y a z = μ · b z

Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.

Если ненулевые векторы a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) коллинеарны, то согласно векторному определению произведения a → × b → = 0 → . И это также соответствует равенству: i → j → k → a x a y a z b x b y b z = 0 → , что, в свою очередь, возможно только тогда, когда заданные векторы связаны соотношениями b → = λ · a → и a → = μ · b → , где μ — произвольное действительное число (на основании теоремы о ранге матрицы), что указывает на факт коллинеарности векторов.

Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

Рассмотрим применение условия коллинеарности на конкретных примерах.

Исходные данные: векторы a → = ( 3 — 2 2 , 1 ) и b → = ( 1 2 + 1 , 2 + 1 ) . Необходимо определить, коллинеарны ли они.

Решение

Выполним задачу, опираясь на условие коллинеарности векторов на плоскости в координатах: b x = λ · a x b y = λ · a y Подставив заданные значения координат, получим: b x = λ · a x ⇔ 1 2 + 1 = λ · ( 3 — 2 2 ) ⇒ λ = 1 ( 2 + 1 ) · ( 3 — 2 2 ) = 1 3 2 — 4 + 3 — 2 2 = 1 2 — 1 b y = λ · a y ⇔ 2 + 1 = 1 2 — 1 · 1 ⇔ ( 2 + 1 ) · ( 2 — 1 ) = 1 ⇔ 1 ≡ 1

Т.е. b → = 1 2 — 1 · a → , следовательно, заданные векторы коллинеарны.

Ответ: заданные векторы коллинеарны.

Исходные данные: векторы a → = ( 1 , 0 , — 2 ) и b → = ( — 3 , 0 , 6 ) . Необходимо убедиться в их коллинеарности.

Решение

Т.к. b x = λ · a x b y = λ · a y b z = λ · a z ⇔ — 3 = — 3 · 1 0 = — 3 · 0 6 = — 3 · ( — 2 ) , то верным будет равенство: b → = — 3 · a → , что является необходимым и достаточным условием коллинеарности. Таким образом, заданные векторы коллинеарны.

Найдем также векторное произведение заданных векторов и убедимся, что оно равно нулевому вектору: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 1 0 — 2 — 3 0 6 = i → · 0 · 6 + j → · ( — 2 ) · ( — 3 ) + k → · 1 · 0 — k → · 0 · ( — 3 ) — j → · 1 · 6 — i → · ( — 2 ) · 0 = 0 → Ответ: заданные векторы коллинеарны.

Исходные данные: векторы a → = ( 2 , 7 ) и b → = ( p , 3 ) . Необходимо определить, при каком значении p заданные векторы будут коллинеарны.

Решение

Согласно выведенному выше условию, векторы коллинеарны, если

b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7

тогда λ = 3 7 , а p = λ · 2 ⇔ p = 6 7 .

Ответ: при p = 6 7 заданные векторы коллинеарны.

Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.

Исходные данные: вектор a → = ( 2 , — 6 ) . Необходимо найти любой ненулевой вектор, коллинеарный заданному.

Решение

Ответом может послужить, например, 1 2 · a → = ( 1 , — 3 ) или вектор 3 · a → = ( 6 , — 18 ) .

Ответ: вектор, коллинеарный заданному имеет координаты ( 1 , — 3 ) .

Исходные данные: вектор a → = ( 3 , 4 , — 5 ) . Необходимо определить координаты вектора единичной длины, коллинеарного заданному.

Решение

Вычислим длину заданного вектора по его координатам: a → = a x 2 + b x 2 + c x 2 = 3 2 + 4 2 + ( — 5 ) 2 = 5 2 Разделим каждую из заданных координат на полученную длину и получим единичный вектор, коллинеарный данному: 1 a → · a → = ( 3 5 2 , 4 5 2 , — 1 2 )

Видео:Коллинеарные векторы.Скачать

Разработка урока по теме «Применение векторов к решению задач. Средняя линия трапеции».

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:§15 Коллинеарность векторовСкачать

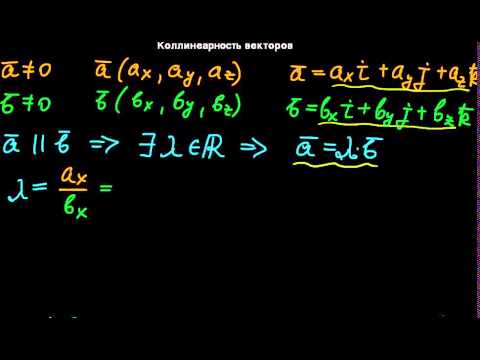
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Г – 9 класс Урок № 7

Тема: «Применение векторов к решению задач. Средняя линия трапеции».

Дидактическая: на конкретных примерах показать применение векторов при решении геометрических задач; ввести понятия средней линии трапеции; доказать теорему о средней линии трапеции с помощью векторов.

Развивающая: развивать логическое мышление учащихся, учить решать задачи; развивать воображение – репродуктивное, творческое, образное; абстрактное мышление, умение обобщать.

Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.

Знать, действия производимые с векторами, понятие средней линии трапеции, теорему о средней линии трапеции.

Уметь вычислять среднюю линию трапеции, решать задачи с помощью векторов.

Сообщение темы и целей урока.

Актуализация знаний и умений обучающихся.

Проверка выполнения домашнего задания. Разбор нерешенных заданий.

Повторение изученного материала.

1. Ответить на вопросы на с. 213–214.

2. Проверка усвоения учащимися материала.

1. Устно ответить на вопросы:

1) Какие векторы называются коллинеарными? Изобразите на рисунке сонаправленные векторы и и противоположно направленные векторы и .

2) Какой вектор называется произведением данного вектора на данное число?

3) Могут ли векторы и быть неколлинеарными?

4) Сформулируйте основные свойства умножения вектора на число.

2. Решить задачу на доске и в тетрадях по готовому чертежу:

Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM : MD = BN : NC = 3 : 4.

Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.

Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно задаче 2 из п. 84 имеем . Из условия следует, что , поэтому .

Таким образом, векторы и коллинеарные, и, значит, точки K1, K2 и K3 лежат на одной прямой.

Изучение нового материала.

1. Определение трапеции. Виды трапеций.

2. Определение средней линии трапеции.

3. Доказательство теоремы о средней линии трапеции.

Доказательство оформить на доске и в тетрадях в виде следующей краткой записи:

Дано: ABCD – трапеция, AD || BC, M – середина стороны AB; N – середина стороны CD (рис. 266 учебника).

Доказать: MN || AD, MN = .

1) Согласно рассмотренной в классе задаче 1 .

2) Так как , то и, значит, MN || AD.

3) Так как , то = AD + BC, поэтому MN = (AD + BC).

Формирование умений и навыков.

Работа по учебнику.

1. Векторы могут использоваться для решения геометрических задач. Рассмотрим вспомогательную задачу.

2. Разобрать решение задачи 1 на с. 208 учебника по рис. 264.

3. Решить задачу 2. Точки M и N – середины сторон AB и CD четырехугольника ABCD. Докажите, что

Пусть О – произвольная точка. Согласно задаче 1 из п. 84 имеем поэтому .

Примечание. Результат задачи 2 можно использовать при доказательстве теоремы о средней линии трапеции на следующем уроке.

4. 1. Решить на доске и в тетрадях задачу № 793.

Пусть a и b – основания трапеции, тогда а + b = 48 – (13 + 15) = 20 (см); средняя линия MN = = 10 (см).

2. Решить задачу № 795.

3. Решить задачу № 799 на доске и в тетрадях.

Пусть BK – перпендикуляр, проведенный к основанию AD данной трапеции.

Тогда KD = AD – AK.

Но AK = , поэтому KD = AD – , то есть отрезок KD равен средней линии трапеции. Значит, средняя линия трапеции равна 7 см.

5. Решить задачу 3. Точка С лежит на отрезке AB, причем АС : СВ = 2 : 3. Докажите, что для любой точки О справедливо равенство

По условию AC:CB=2 : 3,поэтому Но Следовательно, откуда получается

Примечание. Задача 3 является частным случаем более общей задачи 806.

6. Решить задачу № 786 на доске и в тетрадях.

Так как точка А1 – середина стороны ВС, то .

7. При наличии времени решить задачу 4.

Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.

Пусть О – произвольная точка. Согласно задаче 1 из п. 84 . Аналогично, .

Из этих равенств следует, что Отсюда следует, что PQ || AE и PQ = AE.

Подвести итоги урока, выставить отметки обучающимся за урок.

В результате изучения параграфа обучающиеся должны знать, какой вектор называется произведением вектора на число; уметь формулировать свойства умножения вектора на число; знать, какой отрезок называется средней линией трапеции; уметь формулировать и доказывать теорему о средней линии трапеции; уметь решать задачи типа №№ 782–787; 793–799.

Домашнее задание: изучить материал п. 87, 88; ответить на вопросы 18–20, с. 214 учебника; решить задачи №№ 787, 794, 796.