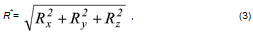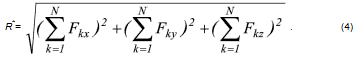Равнодействующая системы сходящихся сил приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Система сходящихся сил
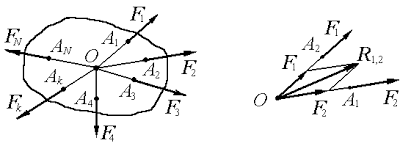
Пусть, к абсолютно твердому телу приложена система N сил (F1, F2, … FN), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).
Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.
Видео:Сложение нескольких векторов. Правило многоугольникаСкачать

Приведение к равнодействующей
Докажем, что данная система сил эквивалентна одной силе, т.е. приводится к равнодействующей силе.
В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.
Далее, по четвертой аксиоме, силы F1 и F2 можно заменить их равнодействующей R1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.
Далее можно записать аналогичные соотношения для полученной равнодействующей силы R * 1,2 и силы F3, тогда
Для системы N сил окончательно будем иметь
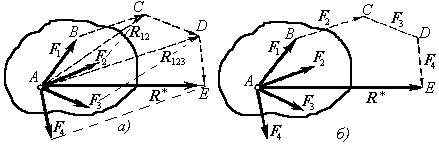
На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.
Силовой многоугольник
Из конца вектора силы F1 (точки В) проводим вектор ВС, геометрически равный силе F2. Из конца этого вектора (точки С) проводим вектор СD равный силе F3. Из конца этого вектора (точки D) проводим вектор DE, равный силе F4.
Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.
Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.
Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.
Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.
Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.
Видео:Построение силового многоугольникаСкачать

Вычисление равнодействующей
Для аналитического определения равнодействующей найдем ее проекции Rx, Ry, Rz на оси декартовой системы координат. Имеем
Тогда величина равнодействующей определится следующей формулой:
Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:
Здесь α , β , γ — углы между положительным направлением осей координат и равнодействующей.
Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.
В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Видео:Вычитание векторов. 9 класс.Скачать

ПЛОСКАЯ СИСТЕМА СХОДЯЩИХСЯ СИЛ
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Геометрический метод сложения сил, приложенных в одной точке
Силы называют сходящимися, если их линии действия пересекаются в одной точке. Различают плоскую систему сходящихся сил, когда линии действия всех данных сил лежат в одной плоскости, и пространственную систему сходящихся сил, когда линии действия сил лежат в разных плоскостях.
На основании следствия из третьей аксиомы силу можно переносить по линии ее действия, поэтому сходящиеся силы всегда можно перенести в одну точку — в точку пересечения их линий действия^ Выполнив перенос, на рис. 8, а получим четыре силы -^2’ -^3, ^4, приложенные к точке К. Для определения их равнодействующей сложим последовательно все данные силы, используя правило треугольника (рис. 8, б).
Находим частичные равнодействующие:
и, наконец, сложив все силы, определяем полную равнодействующую
Промежуточные векторы F12 и -^123 можно не строить, а последовательно, в указанном выше порядке одну за другой отложить все заданные силы и начало первой соединить с концом последней. Фигура OABCD (см. рис. 8, б) называется силовым многоугольником. Замыкающая сторона этого многоугольника представляет собой равнодействующую F^ заданной системы сил, равную их геометрической сумме. Необходимо обратить внимание на то, что равнодействующая сила F^ всегда направлена от начала первого слагаемого к концу последнего слагаемого. Иными словами, стрелка равнодействующей силы всегда направлена навстречу обходу многоугольника, соответствующему последовательному сложению заданных сил (см. рис. 8, б).
Когда при построении силового многоугольника конец последней слагаемой силы совместится с началом первой, равнодейству-
ющая системы сходящихся сил окажется равной нулю. В этом случае система сходящихся сил находится в равновесии.
Самозамыкание силового многоугольника данной системы сходящихся сил является геометрическим условием ее равновесия.
Пример 2. На рис. 9, а показана система четырех сил Flt F2, Fs и F4, приложенных в точке А. Определить, уравновешена ли данная система сил?
Решение. Построение силового многоугольника выполним в последовательности, соответствующей рис. 9, б.
Сохраняя масштаб и направление, из произвольной точки отложим вектор первой силы Д. Из конца первого вектора силы отложим вектор второй силы F2. Аналогично отложим остальные векторы сил F3, Т4. Конец вектора Т4 совпадает с началом вектора
Силовой многоугольник замкнут, равнодействующая равна нулю (Fs = 0); следовательно, система уравновешена.
1. Укажите, какой вектор силового многоугольника (рис. 10) является равнодействующей силой.
2. Какой из многоугольников, представленных на рис. 10 и 11, соответствует уравновешенной системе сходящихся сил?
Видео:8 класс, 44 урок, Законы сложения векторов. Правило параллелограммаСкачать

ПроСопромат.ру
Видео:Сложение векторов. 9 класс.Скачать

Технический портал, посвященный Сопромату и истории его создания
Видео:№764. Пользуясь правилом многоугольника, упростите выражения: а) (АВ + ВС -МС)Скачать

Задача
Укажите, какой вектор силового многоугольника является равнодействующей силой:
Равнодействующая сила в силовом многоугольнике всегда направлена от начала первого слагаемого вектора к концу последнего. Так как векторы ОА, АВ, ВС,СD направлены последовательно один за другим, то ни один из них не может быть равнодействующей силой.
Равнодействующей силой является вектор ОD.
🎦 Видео
Равнодействующая и сложение силСкачать

8 класс, 45 урок, Сумма нескольких векторовСкачать

10 класс, 41 урок, Сумма нескольких векторовСкачать

Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

сложение ВЕКТОРОВ вычитание ВЕКТОРОВ 9 класс геометрия АтанасянСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Разложение вектора по базису. 9 класс.Скачать

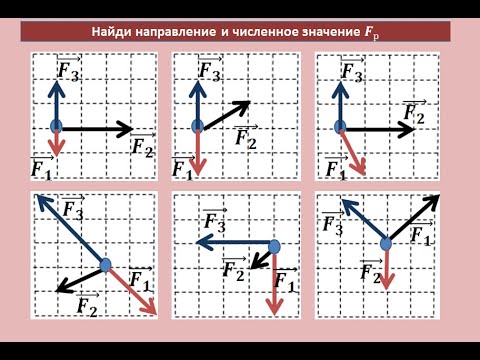
Тренировочные задания по теме: "Результирующая сила"Скачать
Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Все о векторах за 60 минут | Математика ОГЭ | Молодой РепетиторСкачать