Глава 7. Изображение линий на чертежах

Глава 7Образование линийКомплексные чертежи прямых линийРасположение прямой относительно плоскостей проекцийВзаимное расположение двух прямыхОпределение натуральной величины отрезка прямой линииКривые линииВзаимное расположение точки и линииВопросы

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

§ 41. Взаимное расположение двух прямых

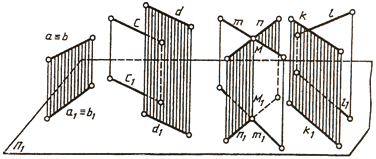
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а ≡ b, быть параллельными с ׀׀ d, пересекаться m ∩ n и скрещиваться (k°/l).

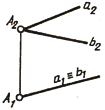
Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.

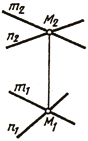
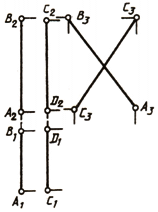
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):

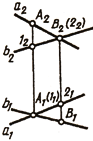
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):

A₁ (1₁) — горизонтально конкурирующие точки;

B₂ (2₂) — фронтально конкурирующие точки.

В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):

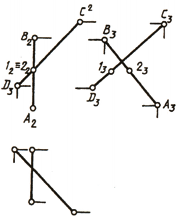
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, 6) окажутся профильными прямыми, то для определения взаимного расположения их необходимо построить третью, профильную проекцию этих прямых.

Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.

Рассматривая рис. 76, б,можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.

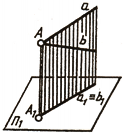
Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а).Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими .

Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б).

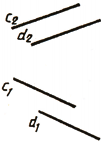
Прямые с и d (рис. 77, в) — фронтально конкурирующие, имеют общую фронтально проецирующую плоскость.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

1. Что представляют собой проекции двух скрещивающихся прямых. Геометрия 10 класс Зив Б.Г. Доп. Самостоятельные работы 1. Вариант 5

1. Что представляют собой проекции двух скрещивающихся прямых на плоскости?

1. Что из себя представляют проекции двух скрещивающихся прямых на плоскости?
Решение:
Если одна из них перпендикулярна плоскости, то проекцией будут прямая и точка, иначе — две пересекающиеся или параллельные прямые. Две пересекающиеся прямые, две параллельные прямые, прямая и точка.

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Чертежик

Метки

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Взаимное расположение прямых линий

Взаимное расположение прямых линий может быть представлено следующим образом: быть параллельными, пересекаться, скрещиваться.

1. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость проекций (не перпендикулярную данным прямым) — параллельны.

Пересекающимисяназываются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Прямые пересекаются, если их одноименные проекции также пересекаются, а проекции точки пересечения лежат на одной линии связи.

Скрещивающимисяназываются две прямые не лежащие в одной плоскости.

Прямые скрещиваются, если они не пересекаются и не параллельны между собой, а точки пересечения их одноименных проекций не лежат на одной линии связи.

Примеры выполненных чертежей смотрите в этом разделе .