Видео:Параллельные прямые | Математика | TutorOnlineСкачать
Прямые на координатной плоскости
 Линейная функция |
| График линейной функции |
| Прямые, параллельные оси ординат |
| Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые |
Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать
Линейная функция
Линейной функцией называют функцию, заданную формулой
| y = kx + b, | (1) |
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
 |
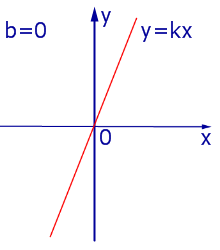| Рис.1 |
 |
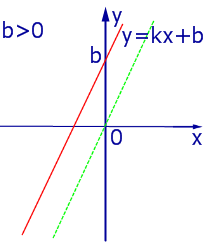| Рис.2 |
 |
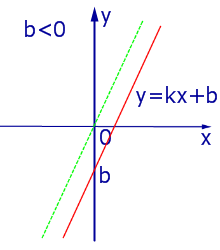| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
 |
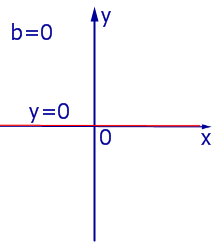| Рис.4 |
 |
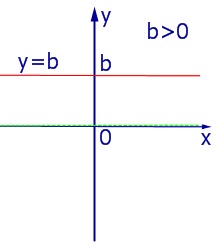| Рис.5 |
 |
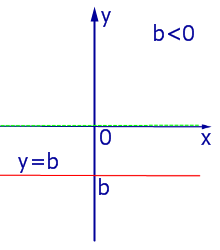| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
| k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены имеющие разные угловые коэффициенты y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При
Видео:9 класс, 7 урок, Уравнение прямойСкачать  Прямые, параллельные оси ординатПрямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа. В случае, когда
что и требовалось. В случае, когда
откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости:
В случае, когда Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство Видео:Математика без Ху!ни. Уравнение плоскости.Скачать  1 .Выберите уравнение, с помощью которого задана линейная функцияу= х² + 8х 2.Если k= — 9 и b = — 9, то линейная функция имеет вид у = — 9х — 9 3.Выберите функцию график, которой расположен в I и III координатных четвертях у = — х + 9 4.Найдите значение функции у = 2х -12 в точке, абсцисса которой равна 4 5.Какой из указанных прямых принадлежит точка А (-3; 8) у= — 3х+ 8 6.Определите угловой коэффициент функции, заданной уравнением у = 1,2 — 7х 7.Определите точку, которая принадлежит графику функции, заданной уравнением у= 5 — 2х 8.Укажите ложное утверждение график функции у = 7 расположен в I и II координатных четвертях 9.Для функции у = 1/4 х + 1,5 укажите ложные утверждения это — линейная функция 10.Выберите точку, в которой график функции у= — 0,75х — 5 пересекает ось ординат Видео:12. Уравнения прямой в пространстве Решение задачСкачать  Прямая линия. Уравнение прямой.Свойства прямой в евклидовой геометрии. Через любую точку можно провести бесконечно много прямых. Через любые две несовпадающие точки можно провести единственную прямую. Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или являются параллельными (следует из предыдущего). В трёхмерном пространстве существуют три варианта взаимного расположения двух прямых:
Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение). Общее уравнение прямой. Определение. Любая прямая на плоскости может быть задана уравнением первого порядка причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А, В и С возможны следующие частные случаи: • C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат • А = 0, В ≠0, С ≠0 — прямая параллельна оси Ох • В = 0, А ≠0, С ≠ 0 – прямая параллельна оси Оу • В = С = 0, А ≠0 – прямая совпадает с осью Оу • А = С = 0, В ≠0 – прямая совпадает с осью Ох Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных Уравнение прямой по точке и вектору нормали. Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1). Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0. Уравнение прямой, проходящей через две точки. Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:
Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель. На плоскости записанное выше уравнение прямой упрощается:
Дробь Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту. Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить уравнением прямой с угловым коэффициентом k. Уравнение прямой по точке и направляющему вектору. По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой. Определение. Каждый ненулевой вектор Аα1 + Вα2 = 0 называется направляющим вектором прямой. Пример. Найти уравнение прямой с направляющим вектором Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям: 1 * A + (-1) * B = 0, т.е. А = В. Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение: Уравнение прямой в отрезках. Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу. Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках. С = 1, Нормальное уравнение прямой. Если обе части уравнения Ах + Ву + С = 0 разделить на число нормирующем множителем, то получим xcosφ + ysinφ — p = 0 – нормальное уравнение прямой. 📽️ ВидеоМатематика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  Уравнение параллельной прямойСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  №976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать  Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать  Составляем уравнение прямой по точкамСкачать  Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать  Видеоурок "Канонические уравнения прямой"Скачать  №933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать  Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать  4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать  1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать  Написать канонические и параметрические уравнения прямой в пространствеСкачать  |
, параллельны .
, пересекаются при любых значениях свободных членов.
прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле
уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .
получаем:
уравнение (5) решений вообще не имеет.
= k называется угловым коэффициентом прямой.
, то полученное уравнение называется
(α1, α2), компоненты которого удовлетворяют условию
(1, -1) и проходящей через точку А(1, 2).
или 
, где
, а = -1, b = 1.
, которое называется