Какое из следующих утверждений верно?
1) Все углы ромба равны.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
В ответ запишите номер выбранного утверждения.
Рассмотрим каждое из утверждений:
1) «Все углы ромба равны» — неверно. Верно только в случае квадрата.
2) «Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны» — неверно. Стороны квадрата и ромба могут быть равны, однако такие четырёхугольники не равны.
3) «Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности» — верно.
Видео:Какие из УТВЕРЖДЕНИЙ верны? Решаем задание 19 из ОГЭ, 1 частьСкачать

Решение №2222 Какое из следующих утверждений верно? 1) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника …
Какое из следующих утверждений верно?
1) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
2) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
3) Смежные углы равны.
В ответ запишите номер выбранного утверждения.
Источник: ОГЭ Ященко 2022 (50 вариантов)
1) не верно , у этих четырёхугольников могут быть разные углы:

2) верно , существует такая формула, для любого параллелограмма (ромб является параллелограммом):
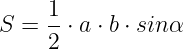
Ответ: 2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:Какие из СЛЕДУЮЩИХ УТВЕРЖДЕНИЙ верны? Решаем задание 19 из ОГЭ, 4 частьСкачать
Подготовка к ОГЭ. Задача № 20
Разделы: Математика
Цели: повторение и закрепление, практическое применение усвоенных теоретических знаний при решении заданий модуля геометрия, № 20.
Задачи:
- Сформировать у учащихся умение использовать приобретенные знания для решения заданий разной направленности;
- Отрабатывать теоретические геометрические знания;
- Отработать навыки решения заданий различного типа.
- Развивать и совершенствовать умения применять накопленные знания в измененной ситуации, делать выводы и обобщения.
- Подготовка к ОГЭ, воспитывать настойчивость в достижении поставленной цели.
Оборудование: мультимедийная установка, презентация.
Ход урока
Организационный момент
1. Актуализация знаний.
Краткие методические рекомендации
Задание 20 ОГЭ по математике заключается в выборе одного или нескольких верных утверждений из множества данных (в настоящее время — из трёх данных). В большинстве случаев правильный ответ на вопрос задачи связан со знанием простейших геометрических фактов и утверждений. Такие задачи позволяют организовать экспресс повторение большинства определений и теорем школьного курса геометрии с целью быстрой диагностики имеющихся пробелов в знания и последующего устранения этих пробелов. В качестве примеров рассмотрим чуть более сложные задания на выбор верных утверждений из шести данных.
Пример 1. Укажите в порядке возрастания без пробелов, запятых и прочих дополнительных символов номера верных утверждений.
1) Существует прямоугольник, диагонали которого различны.
2) В любом прямоугольнике диагонали равны.
3) Существует ромб, диагонали которого различны.
4) В любом ромбе диагонали равны.
5) Существует трапеция, диагонали которой различны.
6) В любой трапеции диагонали равны.
Решение: По свойству прямоугольника второе утверждение является верным, а первое—нет. Аналогично из оставшихся утверждений верными являются 3 и 5.
Ответ. 235.
Пример 2. Укажите в порядке возрастания без пробелов, запятых и прочих дополнительных символов номера верных утверждений.
1) Существует выпуклый четырёхугольник, все углы которого острые.
2) В любом выпуклом четырёхугольнике все углы острые.
3) Существует выпуклый четырёхугольник, все углы которого прямые.
4) В любом выпуклом четырёхугольнике все углы прямые.
5) Существует выпуклый четырёхугольник, все углы которого тупые.
6) В любом выпуклом четырёхугольнике все углы тупые.
Ответ. Первое утверждение не является верным, поскольку сумма любых четырёх острых углов меньше 360◦ — суммы углов выпуклого четырёхугольника. Второе утверждение не является верным, пример — квадрат. Третье утверждение является верным, пример — прямоугольник. Четвёртое утверждение не является верным, пример — трапеция. Пятое утверждение не является верным, поскольку сумма любых четырёх тупых углов больше 360◦ — суммы углов выпуклого четырёхугольника. По этой же причине не является верным и шестое утверждение.
Ответ. 3.
Формулировка темы и целей урока.
2. Закрепление знаний
Подготовительные задачи
1. Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
2. Какое из следующих утверждений верно?
2) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
3) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
В ответе запишите номер выбранного утверждения.
3. Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению его диагоналей.
2) В параллелограмме есть два равных угла.
3) Боковые стороны любой трапеции равны.
В ответе запишите номер выбранного утверждения.
4. Какое из следующих утверждений верно?
1) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.
2) Площадь параллелограмма равна половине произведения его диагоналей.
3) Вписанный угол, опирающийся на диаметр окружности, прямой.
В ответе запишите номер выбранного утверждения.
5. Какие из следующих утверждений верны?
1) Существуют три прямые, которые проходят через одну точку.
2) Боковые стороны любой трапеции равны.
3) Сумма углов равнобедренного треугольника равна 180 градусам.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
6. Какие из следующих утверждений верны?
1) Треугольника со сторонами 1 см, 2 см, 4 см не существует.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Все диаметры окружности равны между собой.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
7. Какое из следующих утверждений верно?
1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) В параллелограмме есть два равных угла.
3) Сумма углов любого треугольника равна 360 градусам.
В ответе запишите номер выбранного утверждения.
8. Какие из следующих утверждений верны?
1) Любые два равносторонних треугольника подобны.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Все диаметры окружности равны между собой.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
9. Какие из следующих утверждений верны?
1) Существует квадрат, который не является прямоугольником.
2) Если в параллелограмме две соседние стороны равны, то этот параллелограмм является ромбом.
3) Все диаметры окружности равны между собой.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
10. Какое из следующих утверждений верно?
1) Любой параллелограмм можно вписать в окружность.
2) Касательная к окружности параллельна радиусу, проведённому в точку касания.
3) Сумма острых углов прямоугольного треугольника равна 90 градусам.
В ответе запишите номер выбранного утверждения.
3. Зачетные задачи
1. Какие из следующих утверждений верны?
1) В прямоугольном треугольнике гипотенуза равна сумме катетов.
2) Если в ромбе один из углов равен 90 градусам, то этот ромб является квадратом.
3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
2. Какое из следующих утверждений верно?
1) Любой прямоугольник можно вписать в окружность.
2) Все углы ромба равны.
3) Треугольник со сторонами 1, 2, 3 существует.
В ответе запишите номер выбранного утверждения.
3. Какое из следующих утверждений верно?
2) Каждая из биссектрис равнобедренного треугольника является его высотой.
3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
В ответе запишите номер выбранного утверждения.
4. Какое из следующих утверждений верно?
1) Основания любой трапеции параллельны.
2) Диагонали ромба равны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
В ответе запишите номер выбранного утверждения.
5. Какие из следующих утверждений верны?
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Средняя линия трапеции параллельна её основаниям.
3) Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
6. Какие из следующих утверждений верны?
1) Средняя линия трапеции равна сумме её оснований.
2) Все углы прямоугольника равны.
3) Существуют три прямые, которые проходят через одну точку.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
7. Какое из следующих утверждений верно?
1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.
2) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3) Смежные углы всегда равны.
В ответе запишите номер выбранного утверждения.
8. Какое из следующих утверждений верно?
1) Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
2) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.
3) Смежные углы всегда равны.
В ответе запишите номер выбранного утверждения.
9. Какие из следующих утверждений верны?
1) В любой прямоугольной трапеции есть два равных угла.
2) Касательная к окружности параллельна радиусу, проведённому в точку касания.
3) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
В ответе запишите номера выбранных утверждений в порядке возрастания без пробелов, запятых и других дополнительных символов.
10. Какое из следующих утверждений верно?
1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Через заданную точку плоскости можно провести только одну прямую.
3) Диагонали ромба точкой пересечения делятся пополам.
В ответе запишите номер выбранного утверждения.
4. Домашнее задание: (ФИПИ, ОГЭ, модуль геометрия, стр 161-164).
💥 Видео
Сторона ромба образует с одной из диагоналей угол 50°. Найдите углы ромба.Скачать

Задание 19 (В1) ОГЭ по математике ▶ №14 (Минутка ОГЭ)Скачать

№407. Найдите углы, которые образуют диагонали ромба с его сторонами, если одинСкачать

ОГЭ, задание 19, найти верное утверждение.Скачать

№405. В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы,Скачать
Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Какие из этих УТВЕРЖДЕНИЙ верны? Решаем задание 19 из ОГЭ, 2 частьСкачать

Найти углы ромбаСкачать
19 ЗАДАНИЕ ОГЭ ДИАГОНАЛИ РОМБА РАВНЫ?Скачать

Найдите углы ромба || ОГЭ по математике №23Скачать

ЕГЭ 3 задача углы ромбаСкачать

Определение углов ромба (Задача 24 ОГЭ-2019 по математике)Скачать

№477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромбаСкачать

Задание 17 ОГЭ по математике. Ромб. Найти высоту ромба.Скачать

19 задание огэ математика 2023 ВСЕ ТИПЫ геометрияСкачать

ШМ. 10.4 ОГЭ по математике. Геометрия первой части. Задания 15,16,17,18,19. ОГЭ 2023.Скачать

Ромб. Свойства ромба. Решение задач.Скачать

№601. Найдите углы ромба с диагоналями 2√3 и 2.Скачать
