Каким может быть расположение двух прямых если обе они параллельны одной плоскости

Возможны четыре различных случая расположения двух прямых в пространстве:

– прямые скрещиваются, т. е. не лежат в одной плоскости;

– прямые пересекаются, т. е. лежат в одной плоскости и имеют одну общую точку;

– прямые параллельны, т. е. лежат в одной плоскости и не пересекаются;

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

(a || b) (прямая а параллельна прямой b)

Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

(Min b, aparallel b)

Два отрезка называются параллельными, если они лежат на параллельных прямых.

отрезок (CD || AB)

Свойства параллельных прямых

1. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

(a capalpha=M, bparallel a Rightarrow bcap alpha)

1. Если две прямые параллельны третьей прямой, то они параллельны.

(aparallel c, bparallel c Rightarrow aparallel b)

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

(asubsetalpha, bcap alpha=K, \ Knotin a Rightarrow a и b — скрещивающиеся прямые)

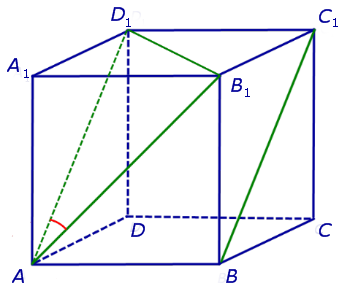
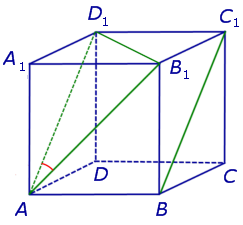
Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых (a и b) .

Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Найдите параллельные прямые.

Определите взаимное расположение прямых (a и b) .

Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания.

1) Прямые СD и MN скрещивающиеся.

2) Прямые АВ и MN лежат в одной плоскости.

3) Прямые СD и MN пересекаются.

4) Прямые АВ и СD скрещивающиеся.

Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?

Две прямые в пространстве называются параллельными, если

Прямая а, параллельная прямой b, пересекает плоскость α. Прямая с параллельна прямой b, тогда

Каким может быть взаимное расположение двух прямых, если обе они параллельны одной плоскости?

Две прямые пересекаются. Что это значит?

Две прямые называются скрещивающимися, если

Взаимное расположение двух прямых в пространстве.
Признак скрещивающихся прямых.
Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Признак скрещивающихся прямых

Угол между скрещивающимися прямыми

Взаимное расположение двух прямых в пространстве

Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.
Две параллельные прямые		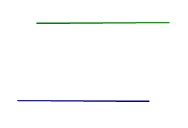Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		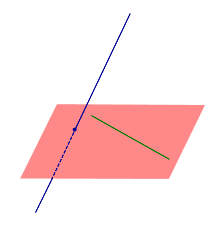Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми , если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми , если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми , если не существует плоскости, содержащей обе прямые.

С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		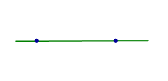Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		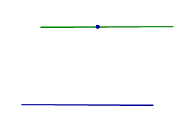Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		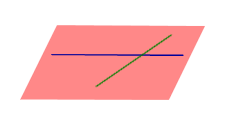Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		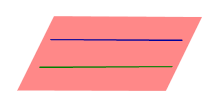Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками
Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых
Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми
Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми
Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

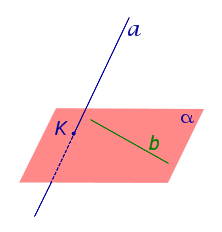
Признак скрещивающихся прямых . Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

Доказательство . Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

Для этого предположим, что прямая a , пересекающая плоскость в точке K , и прямая b , лежащая в плоскости α (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой β и докажем, что плоскость β совпадает с плоскостью α . Действительно, поскольку обе плоскости α и β проходят через прямую b и точку K , не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости . Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость , а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

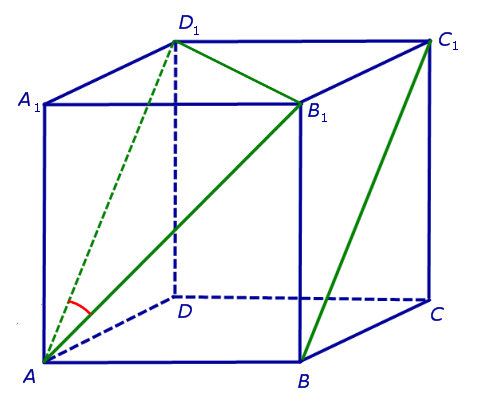
Угол между скрещивающимися прямыми

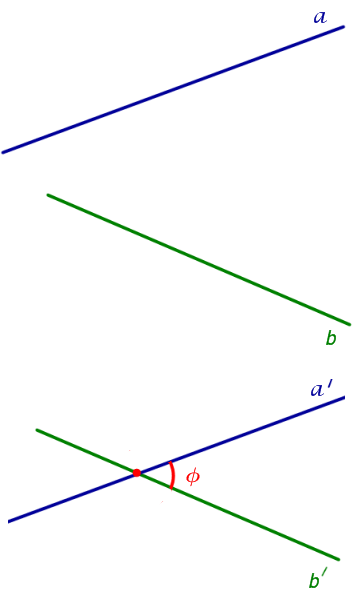
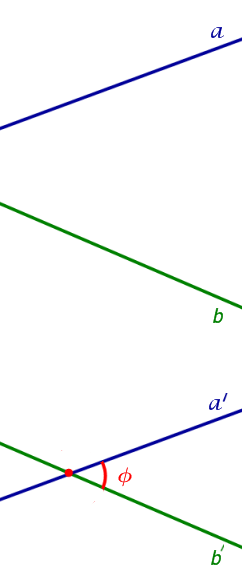
На рисунке 2 изображены скрещивающиеся прямые a и b . Прямая a’ параллельна прямой a , прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b .

Для того, чтобы найти угол между прямыми AB₁ и BC₁ , проведем в кубе диагональ боковой грани AD₁ и диагональ верхнего основания D₁B₁ (рис. 4).

Замечание . Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».

Чертежик

Метки

Взаимное расположение прямых линий

Взаимное расположение прямых линий может быть представлено следующим образом: быть параллельными, пересекаться, скрещиваться.

1. Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость проекций (не перпендикулярную данным прямым) — параллельны.

1. Пересекающимисяназываются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Прямые пересекаются, если их одноименные проекции также пересекаются, а проекции точки пересечения лежат на одной линии связи.

1. Скрещивающимисяназываются две прямые не лежащие в одной плоскости.

Прямые скрещиваются, если они не пересекаются и не параллельны между собой, а точки пересечения их одноименных проекций не лежат на одной линии связи.

Примеры выполненных чертежей смотрите в этом разделе .

🔥 Видео