Разделить окружность на 12 частей без циркуля (5 видео)

Как разделить окружность на 12 частей

Коллеги сегодня попробуем разделить окружность на 12 частей. Продолжим ряд уроков по расчленению кругов на равные части.

В записях сайта есть не мало уроков по делению круга. Вам (художникам) должно вполне хватить. Этот блок статей больше относится к уроку геометрии, но я уверяю, что это жизненно необходимо для рисования разных предметов.

Сегодня будем делить окружность на 12 частей, а другие (подобные) статьи можете посмотреть ниже, перейдя по ссылкам:

Делим круг тремя и шестью одинаковыми отрезками
Деление четырьмя не рассматривалось (понятен по умолчанию)
На 5 одинаковых частей смотрим здесь
Так же разделяли окружность семью отрезками
Присутствует деление на 8 долей
Деление окружности на десять, в нашей записи.

Хочу заметить, что урок очень легкий. Мы сможем без особого труда поделить окружность циркулем.

Зачем нужно разделить круг на двенадцать равных частей это решать вам. Приведу очень простой пример. В картине, которую задумали, присутствует циферблат часов. Это полотно о символе Англии — башни Биг-Бен. А может вы пишите портрет простого депутата (не коррупционера), у которого ручные часы Cartier за 50000 $ .

Для получения таких заказов, где присутствуют циферблаты, вам необходимо знать приемы, а они – геометрические.

Поделим круг фронтально, без разбора перспективы (об этом другие уроки).

Содержание

Разделить окружность на 12 частей циркулем
Деление окружности на любое число равных частей
Термины при построениях окружности
Деление окружности на 4 и 8 одинаковых частей
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
Деление окружности на 5 и 10 равных частей
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
Нахождение центра дуги окружности
Разделить окружность на 12 частей без циркуля
📸 Видео

Видео:КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Разделить окружность на 12 частей циркулем

Нам нужны не сложные инструменты: линейка, карандаш обычный, школьный циркуль, и захватите резинку.

Рисуем окружность и делим ее горизонтальным ТН и вертикальным РМ диаметральными прямыми с центром О. Как правильно начертить диаметры (они должны пройти точно через центр) я писал в заметке: «Как разделить круг на 8 частей».

Сделаем замер циркулем радиуса ТО

Изобразим дугу (зеленая пунктирная кривая). Циркуль ставим в отметку Т и через О наносим часть круга, как фото ниже.

Повторим операцию еще раз. Теперь средина дуги точка Р. Смотрите фотографию внизу.

И еще две дуги проведем через О с центрами Н и М.

Теперь имеем 12 засечек.

И вот у нас круг, разделенный двенадцатью равными отрезками. Смотрите иллюстрацию внизу.

Процедура разделения не очень сложная. Если у кого есть другие способы, пишите.
Так же предлагаю посмотреть урок рисунка арки с одной точкой схода.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление окружности на 12 равных частейСкачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:Деление окружности на n- равные частиСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Как разделить окружность на 12 частей How to divide a circle into 12 partsСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Построение 12 угольника циркулемСкачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Как разделить окружность на равные части!Скачать

Разделить окружность на 12 частей без циркуля

1. Аксонометрические проекции. Прямоугольная изометрическая проекция детали.

2. Приёмы деления окружности на 3, 6, 12 частей с помощью циркуля.

3. По двум видам выполнить вид слева, построить необходимые разрезы. Выполнить технический рисунок детали.

1. Аксонометрические проекции. Прямоугольная изометрическая проекция детали.

Аксонометрические проекции
Чертёж, выполненный в прямоугольных (ортогональных) проекциях, является основным видом изображения, которым пользуются в технике. Для облегчения пространственного представления о предмете иногда применяют аксонометрические проекции. Аксонометрические проекции передают одним изображением пространственную форму предмета. Такое изображение создаёт у человека впечатление, близкое к тому, которое получается при рассмотрении предмета в «натуре». Аксонометрические проекции получаются, если изображаемый предмет вместе с осями координат, к которым он отнесён, с помощью параллельных лучей проецируют на одну плоскость, называемой аксонометрической.
Слово «аксонометрия» переводится «измерение по осям или измерения параллельно осям», так как размеры изображаемого предмета откладываются параллельно осям х, у, z называемым аксонометрическими осями. В зависимости от наклона осей координат х, у, z к аксонометрической плоскости и угла, составляемого проецирующими лучами с этой плоскостью, образуются различные аксонометрические проекции. Если проецирующие лучи перпендикулярны плоскости, то проекция называется прямоугольной. Если проецирующие углы наклонны к плоскости, то проекция называется косоугольной.

Прямоугольная изометрическая проекция
Расположение осей х, у, z в изометрической проекции следующее Ось z проводят вертикально, а оси х и у — под углом 30 к горизонтали. При вычерчивании изометрической проекции размеры по всем трём осям откладывают без сокращения, то есть натуральные

Разделить окружность на 12 частей без циркуля

2. Приёмы деления окружности на 3, 6, 12 частей с помощью циркуля.

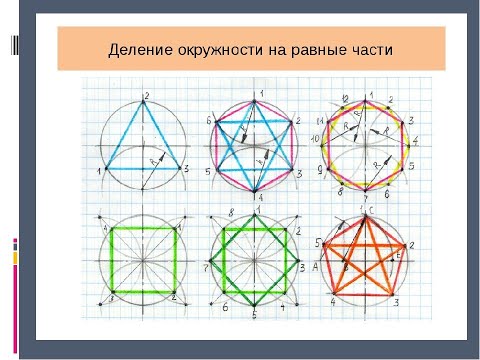
Деление окружности на 3 равные части.
Чтобы разделить окружность радиуса R на 3 равные части и вписать в нее равносторонний треугольник, из точки пересечения диаметра с окружностью (например из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части. Соединив прямыми линиями точки 1, 2, 3 строят вписанный равносторонний треугольник.

Деление окружности на 6 равных частей.
Чтобы разделить окружность на 6 равных частей, из двух противоположных точек (1 и 4) пересечения диаметра с окружностью описывают две дуги радиусом R. Получают точки (2, 3, 5, 6). Вместе с точками которые получились при пересечении диаметра с окружностью он делят окружность на 6 равных частей.

Деление окружности на 12 равных частей.
Для деления окружности на 12 равных частей из четырех точек пересечения осей симметрии с окружностью описывают 4 дуги радиусом R. Полученные точки, вместе с теми, которые получились при пересечении осей симметрии с окружностью, делят окружность на 12 равных частей.