Дан пространственный четырехугольник abcd m и n середины сторон ab и вс соответственно е принадлежит

. Дан пространственный четырехугольникАВСD, М и N середины сторон АВи ВСсоответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

а) Сделайте рисунок к задачке.

б) Обоснуйте, что четырехугольникMNEK есть трапеция.

• Васька Журули
• Геометрия 2019-08-08 13:45:46 7 1

Дано: АВСD-пространственный четырехугольник.

Рассмотрим треугольник АВС:

М-середина АВ, N-середина ВС

Означает, MN-средняя линия треугольника АВС.

Рассмотрим треугольник АDC:

Треугольники ADC и DEK- сходственные (по второму признаку подобия треугольников), т.к угол D-общий, а его стороны пропорциональны:

Если угол 1-го треугольника равен углу иного, а стороны, образующие тот угол в одном треугольнике, пропорциональны подходящим сторонам иного, то такие треугольники сходственны.

А так как два эти треугольника подобны, то КЕAC

Так как KEAC, MNAC =gt; KEMN.

По определению трапеции, четырехугольник именуется трапецией, если две его стороны параллельны, а две иные стороны не параллельны.

Докажем, что стороны КМ, EN не параллельны друг другу.

Означает, стороны KM, EN не могут быть параллельными в связи с различным отношением сторон.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2?

Алгебра | 10 — 11 классы

ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2.

1)Выполните рисунок к задаче.

Рисунок задачи во вложении ниже.

Видео:Решение задач пространственный четырехугольникСкачать

В выпуклом четырехугольнике abcd отмечены точки k l m и n середины сторон ad, ab, bc, cd соответственно?

В выпуклом четырехугольнике abcd отмечены точки k l m и n середины сторон ad, ab, bc, cd соответственно.

Найдите отношение площади четырехугольника abcd к площади четырёхугольника klmn.

Видео:№47. В пространственном четырехугольнике ABCD стороны АВ и CD равны. Докажите, что прямые АВ и CDСкачать

В равнобедренной трапеции ABCD точки F и G являются серединами боковых сторон AB и CD соответственно, отрезок BN — высота трапеции?

В равнобедренной трапеции ABCD точки F и G являются серединами боковых сторон AB и CD соответственно, отрезок BN — высота трапеции.

Найдите периметр четырёхугольника NFGD если средняя линия трапеции равна 10 см, а её боковая сторона — 8 см.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

В параллелограмме ABCD точка M – середина стороны CD, точка К – середина стороны ВС?

В параллелограмме ABCD точка M – середина стороны CD, точка К – середина стороны ВС.

Выразите через векторы А͞В = а͞ и А͞D = b͞ векторы М͞В и К͞М.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Решите задачу, используя круги (диаграммы) Эйлера : множество A состоит из 118 элементов, множество B — из 265 элементов, а множество A пересечённая с B — из 87 элементов Сколько элементов : а) принад?

Решите задачу, используя круги (диаграммы) Эйлера : множество A состоит из 118 элементов, множество B — из 265 элементов, а множество A пересечённая с B — из 87 элементов Сколько элементов : а) принадлежит множеству A, но не принадлежит множеству B б) принадлежит множеству B, но не принадлежит множеству A в) принадлежит множеству A пересечённая с B?

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Не выполняя построение установите принадлежит лиграфику функция Y = sin x + 2?

Не выполняя построение установите принадлежит лиграфику функция Y = sin x + 2.

Видео:Как строить сечения тетраэдра и пирамидыСкачать

Точка А принадлежит плоскости α, точка В не принадлежит плоскости α?

Точка А принадлежит плоскости α, точка В не принадлежит плоскости α.

Принадлежит ли плоскости середина отрезка АВ.

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Найдите площадь трапеции ABCD с основаниями AB и CD, если AB = 10см?

Найдите площадь трапеции ABCD с основаниями AB и CD, если AB = 10см.

Видео:3 правила для вписанного четырехугольника #shortsСкачать

Верно ли , что : а) — 4 принадлежит N ; — 4 принадлежит Z» — 4 принадлежит Q ; б) 5, 6 не принадлежит N ; 5, 6 не принадлежит Z ; 5, 6 не принадлежит Q в) 28 принадлежит N ; 28 принадлежит Z ; 28 прин?

Верно ли , что : а) — 4 принадлежит N ; — 4 принадлежит Z» — 4 принадлежит Q ; б) 5, 6 не принадлежит N ; 5, 6 не принадлежит Z ; 5, 6 не принадлежит Q в) 28 принадлежит N ; 28 принадлежит Z ; 28 принадлежит Q?

Видео:#235. МЕТОДЫ СУЛТАНОВА в задачах с параметромСкачать

Не выполняя построений выясните принадлежит ли точка А(2 ; — 17) графику функций у = — 4х — 9?

Не выполняя построений выясните принадлежит ли точка А(2 ; — 17) графику функций у = — 4х — 9.

Видео:Как строить сечения параллелепипедаСкачать

Не выполняя построения, ответьте на вопрос : графику какой функции у = х2 или у = — х2 принадлежит заданная точка : а) А ( — 2 ; — 4), В( — 3 ; 9)?

Не выполняя построения, ответьте на вопрос : графику какой функции у = х2 или у = — х2 принадлежит заданная точка : а) А ( — 2 ; — 4), В( — 3 ; 9).

Вы перешли к вопросу ВЫПОЛНИТЕ ЧЕРТЁЖ К ЗАДАЧЕ Дан пространственный четырёхугольник ABCD, M и N — середины сторон AB и BC соответственно, E принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2?. Он относится к категории Алгебра, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Алгебра. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

Видео:ПЕТР ЗЕМСКОВ. ЗАДАЧА ПРО ТРАПЕЦИЮ И РАЗГОВОРЫСкачать

Дан пространственный четырехугольник abcd m середина ab

Дан пространственный четырёхугольник ABCD, M и N — середины сторон АВ и ВС соответственно; Е принадлежит CD, K принадлежит DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
Докажите, что четырёхугольник MNEK трапеция

• Попроси больше объяснений
• Следить
• Отметить нарушение

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Ответ

Проверено экспертом

Пространственный четырехугольник — это выпуклый четырехугольник, «согнутый» по одной из диагоналей. При этом он похож на треугольную пирамиду без основания и одной из граней.

Через любые три точки можно провести плоскость. Точки А, В и С, как и точки А, D и C, определяют плоскости треугольников АВС и ADC.

По условию диагонали АС=ВD.

M и N середины АВ и ВС. ⇒ MN — средняя линия треугольника АВС, равна половине диагонали АС и параллельна ей. MN=AC:2

В ∆ АDC точка точка К не середина АD. Аналогично в ∆ BDC т.Е не середина DC. Поэтому КЕ не является средней линией ∆ ADC,

Из отношения DK:KA=DE:EC=1:2 следует подобие ∆ DKE и ∆ DAC.

КЕ Четырехугольник MNEK – трапеция, что и требовалось доказать.

Примерная контрольная. Тема «Параллельность прямых» 10 класс. По Л. С. Атанасяну

Основание трапеции лежит в плоскости . Через точки и проведены параллельные прямые, пересекающие плоскость а в точках и соответственно.

Каково взаимное расположение прямых и ?

Чему равен угол между прямыми и , если ? Ответ обоснуйте.

Дан пространственный четырехугольник , в котором диагонали и равны. Середины сторон этого четырехугольника соединены последовательно отрезками.

Выполните рисунок к задаче.

Докажите, что полученный четырехугольник – ромб.

Треугольники и лежат в разных плоскостях и имеют общую сторону . Точка – середина стороны , точка – середина .

Каково взаимное расположение прямых и ?

Чему равен угол между прямыми и , если и ? Ответ обоснуйте.

Дан пространственный четырехугольник , и – середины сторон и соответственно, , , , .

Выполните рисунок к задаче.

Докажите, что четырехугольник – трапеция.

Примерная контрольная работа. Тема «Параллельность прямых» 10 класс. По А. В. Погорелову

Точки , , , не лежат в одной плоскости. Могут ли прямые и пересекаться?

Через точки , и середину отрезка проведены параллельные прямые, пересекающие некоторую плоскость ось в точках , , соответственно. Найдите длину отрезка , если , , причем отрезок не пересекает плоскость .

Точка не лежит в плоскости трапеции с основаниями и . Докажите, что прямая, проходящая через середины отрезков и , параллельна средней линии трапеции.

Прямые и не лежат на одной плоскости. Могут ли прямые и пересекаться? (Ответ обоснуйте).

Через точки , и середину отрезка проведены параллельные прямые, пересекающие некоторую плоскость а в точках , , соответственно. Найдите длину отрезка , если , , причем отрезок не пересекает плоскость .

Точка не лежит в плоскости параллелограмма . Докажите, что прямая, проходящая через середины отрезков и , параллельна стороне параллелограмма.

Контрольная работа. Тема: «Параллельность прямых и плоскостей». 10 класс. По Л. С. Атанасяну

Прямые и лежат в параллельных плоскостях и . Могут ли эти прямые быть:

Сделайте рисунок для каждого возможного случая.

Через точку , лежащую между параллельными плоскостями и , проведены прямые и . Прямая пересекает плоскости и в точках и соответственно, прямая – в точках , и . Найдите длину отрезка , если , .

Изобразите параллелепипед и постройте его сечение плоскостью, проходящей через точки , и , являющиеся серединами ребер , и .

Прямые и лежат в пересекающихся плоскостях и . Могут ли эти прямые быть:

Сделайте рисунок для каждого возможного случая.

Через точку , не лежащую между параллельными плоскостями и , проведены прямые и . Прямая пересекает плоскости и в точках и соответственно, прямая – в точках и . Найдите длину отрезка , если .

Изобразите тетраэдр и постройте его сечение плоcкостью, проходящей через точки и , являющиеся серединами ребер и , и точку , такую, что , .

Примерная контрольная работа. Тема «Многогранники» По А. С. Атанасяну

Основанием пирамиды является правильный треугольник , сторона которого равна . Ребро перпендикулярно к плоскости , а плоскость составляет с плоскостью угол 30°. Найдите площадь боковой поверхности пирамиды.

Основанием прямого параллелепипеда является ромб , сторона которого равна и угол равен 60°. Плоскость составляет с плоскостью основания угол 60°. Найдите:

площадь боковой поверхности параллелепипеда;

площадь поверхности параллелепипеда.

Основанием пирамиды является квадрат , ребро перпендикулярно к плоскости основания, . Найдите площадь поверхности пирамиды.

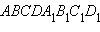
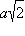
Основанием прямого параллелепипеда является параллелограмм , стороны которого равны и , острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

меньшую высоту параллелограмма;

угол между плоскостью и плоскостью основания;

площадь боковой поверхности параллелепипеда;

площадь поверхности параллелепипеда.

Примерная контрольная работа. Тема «Призма. Параллелепипед» 11 класс. По А. В. Погорелову

Найдите высоту правильной шестиугольной призмы (можно дать обозначение призмы: , если сторона ее основания равна , а меньшая из диагоналей – .

Найдите сторону основания и высоту правильной четырехугольной призмы, если площадь ее полной поверхности равна , а боковая поверхность – .

В прямом параллелепипеде с высотой стороны основания равны и , диагональ . Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины и .

Найдите высоту правильной шестиугольной призмы, если сторона ее основания равна , а большая из диагоналей – .

Найдите сторону основания и высоту правильной четырехугольной призмы, если ее боковая поверхность равна , а полная – .

В прямом параллелепипеде с высотой стороны основания равны и , диагональ . Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины и .

При пользовании «Инфоуроком» вам не нужно платить за интернет!

Минкомсвязь РФ: «Инфоурок» включен в перечень социально значимых ресурсов .

Описание презентации по отдельным слайдам:

Пространственый четырехугольник. Решение задач. гимназия 64 учитель математики Котельникова Н. В.

Доказательство Пусть нам дан пространственный четырехугольник ABCD. M, N, K, L – середины ребер BD, AD, AC, BC соответственно. Нужно доказать, что MNKL – параллелограмм. Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине. Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине. И МN, и LК параллельны АВ. Значит, МN параллельна LК по теореме о трех параллельных прямых. Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать.

Четырехугольник называется пространственным, если его вершины не лежат в одной плоскости. № 1.

Бесплатный
Дистанционный конкурс «Стоп коронавирус»

• Котельникова Наталья ВячеславовнаНаписать 0 07.01.2019

Номер материала: ДБ-345782

Добавляйте авторские материалы и получите призы от Инфоурок

Еженедельный призовой фонд 100 000 Р

«Развитие эмоционального интеллекта»

Спикер: Анна Быкова (#лениваямама)

07.01.2019 235

07.01.2019 135

07.01.2019 169

07.01.2019 216

07.01.2019 245

05.01.2019 83

30.12.2018 404

29.12.2018 174

Не нашли то что искали?

Как организовать дистанционное обучение во время карантина?

Помогает проект «Инфоурок»

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

📸 Видео

Задание №43 — ГДЗ по геометрии 10 класс (Атанасян Л.С.)Скачать

№14 из профильного ЕГЭ по математике. Как строить сечения на изи. Серия-1Скачать

Стереометрия 10 класс. Часть 2 | Математика | TutorOnlineСкачать

№382. Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольникСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Разбор 4 задания | ОГЭ по информатике 2021Скачать

СРЕДНЯЯ ЛИНИЯ. ТРАПЕЦИЯ. ВПИСАННЫЕ И ОПИСАННЫЕ ЧЕТЫРЕХУГОЛЬНИКИ. Контрольная № 2 Геометрия 8 классСкачать