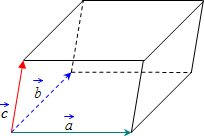
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Видео:44. Правило параллелепипедаСкачать

Правило параллелепипеда. Разложение вектора
Вы будете перенаправлены на Автор24
Видео:10 класс, 44 урок, Правило параллелепипедаСкачать

Правило параллелепипеда
Для правила сложения трех векторов рассмотрим следующую задачу.
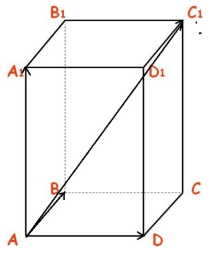
Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$
Доказательство.
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как $overrightarrow=overrightarrow, overrightarrow=overrightarrow$
Из этой задачи получаем следующее правило для нахождения сложения трех векторов. Чтобы найти сумму трех векторов $overrightarrow,overrightarrow и overrightarrow$ нужно от произвольной точки $O$ отложить векторы $overrightarrow=overrightarrow$, $overrightarrow=overrightarrow$ и $overrightarrow=overrightarrow$ и построим параллелепипед на этих векторах. Тогда вектор диагонали $overrightarrow$ и будет суммой этих трех векторов. Это правило называется правилом параллелепипеда для сложения трех векторов.
Видео:Правило параллелепипеда для векторовСкачать

Разложение вектора по двум неколлинеарным векторам
Вспомним сначала, какие векторы называются компланарными.
Два вектора, которые параллельны одной плоскости называются компланарными.
Произвольный вектор $overrightarrow
$ можно разложить по трем некомпланарным векторам $overrightarrow, overrightarrow$ и $overrightarrow$ с единственными коэффициентами разложения.
Математически это можно записать следующим образом
Доказательство.
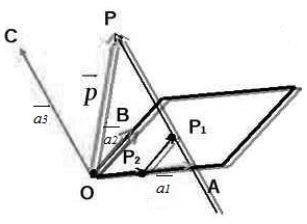
Существование: Пусть нам даны три некомпланарных вектора $overrightarrow, overrightarrow$ и $overrightarrow$. Выберем произвольную точку $O$ и построим следующие векторы:
[overrightarrow=overrightarrow, overrightarrow=overrightarrow, overrightarrow=overrightarrow и overrightarrow
=overrightarrow]
Рассмотрим следующий рисунок:
Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow$. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).
Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow=overrightarrow$, получим:
Так как векторы $overrightarrow$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow
$ и $overrightarrow$ коллинеарны, то
Так как векторы $overrightarrow
$ и $overrightarrow$ коллинеарны, то
Тогда, получаем, что
Существование разложения доказано.
Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow
$ по векторам $overrightarrow, overrightarrow$ и $overrightarrow$:
Вычтем эти разложения друг из друга
Из этого получаем
Теорема доказана.
Видео:Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

Как вычислить вектора в параллелепипеде
4.6. Задачи с решениями
1. В параллелепипеде обозначим . Выразить через векторы a, b, с диагонали параллелепипеда и диагонали граней.
Решение. Сделаем чертёж. Пользуясь правилом сложения векторов, получаем:
AC = AB + AD = b + с, AC1 = AA1 + AC = a + b + с .
Из того же треугольника AA1C получаем: A1C = AC — AA1 = b + с — a.
Чтобы найти B1C, заметим, что B1C = A1D, так как у этих векторов совпадают и длины, и направления. Поэтому B1C = A1D = AD — AA1 = с — a.
Аналогично: DC1 = AB1 = AA1 + AB = a + b .
2. Найти длину и направляющие косинусы вектора AB, если его начало и конец находятся в точках A(7, 6), B(2 — 6).
Решение. Так как каждая точка задана двумя координатами, то рассматривается вектор на плоскости. Находим его координаты, вычитая из координат точки B (конца вектора) координаты точки A (начала вектора): AB = (2 — 7, —6 — 6) = (—5, —12). Находим длину: |AB | = 13, направляющие косинусы: .
3. Найти координату z вектора a = (1, —3, z), если известно, что она отрицательна, а модуль |a| = . Где окажется конец вектора a, если его отложить из точки M(5, —2, 1)?
Решение. По условию, . поэтому ZN = —8.
4. Найти расстояние между точками A(5, —2, 4) и B( —1, 0, 6).
Решение. Расстояние равно длине вектора AB. Найдём:
5. При каких p, q векторы a = (2,p, — 1), b = qi + 9j + 3k будут коллинеарными?
🎬 Видео
Координаты вектора в пространстве. 11 класс.Скачать

№358. Дан параллелепипед ABCDA1B1C1D1. Назовите вектор, начало и конец которого являются вершинамиСкачать

№359. Дан параллелепипед ABCDA1B1C1D1. а) Разложите вектор BD1 по векторам ВА, ВС и ВВ1.Скачать

§20 Нахождение объёма параллелипипедаСкачать

Площадь параллелограмма, построенного на данных векторахСкачать

10 класс, 43 урок, Компланарные векторыСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

№339. Дан параллелепипед ABCDAСкачать

координаты вектора AH, который перпендикуляр из точки A к основанию параллелепипедаСкачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

10 класс, 40 урок, Сложение и вычитание векторовСкачать

№327. На рисунке 97 изображен параллелепипед ABCDA1B1C1D1. Назовите вектор, нСкачать

№330. Нарисуйте параллелепипед ABCDA1B1C1D1 и обозначьте векторы C1D1, BA1Скачать

ГЕОМЕТРИЯ 11 класс: Вектора в пространствеСкачать

1. Векторы и параллелограмм задачи №1Скачать

➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать