Все теоремы о медианах треугольника

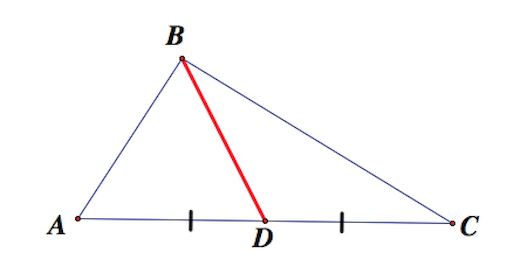
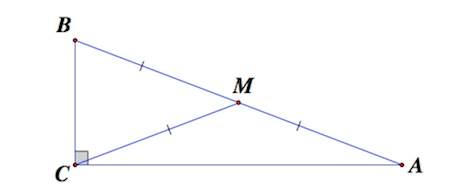
Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

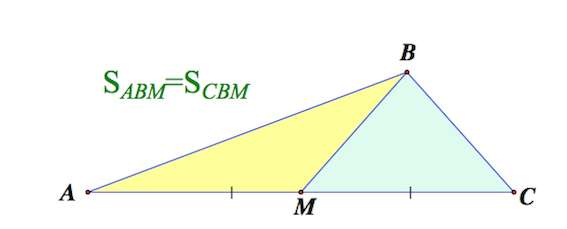
Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

и заметим, что (см. раздел нашего справочника «Площадь треугольника»)

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

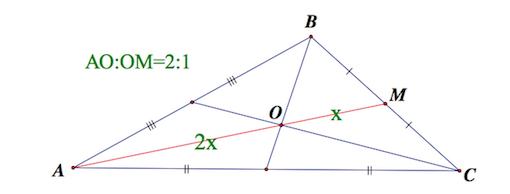
Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

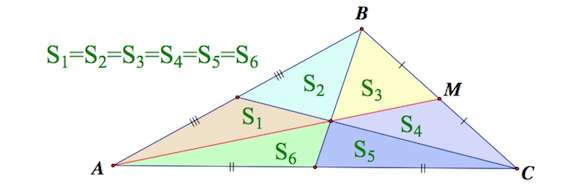
Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Видео:Теорема о трёх медианахСкачать

Элементы треугольника. Медиана

Видео:Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.Скачать

Определение

Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Видео:8. Медиана треугольника и её свойства.Скачать

Свойства

1. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины . Эта точка называется центром тяжести треугольника.

2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)

3. Медианы треугольника делят треугольник на 6 равновеликих треугольников

4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы

5. Длина медианы треугольника вычисляется по формуле:

, где где — медиана к стороне ; — стороны треугольника

6. Длина стороны треугольника через медианы вычисляется по формуле:

, где – медианы к соответствующим сторонам треугольника, — стороны треугольника.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Треугольник

Видео:Теорема о медианеСкачать

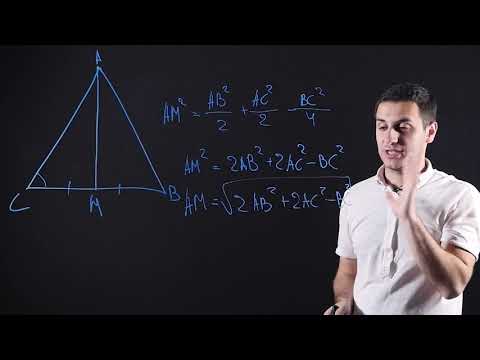
Признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.

3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то треугольники равны.

Видео:Точка пересечения медиан в треугольникеСкачать

Признаки равенства прямоугольных треугольников

1. По двум катетам.

2. По катету и гипотенузе.

3. По гипотенузе и острому углу.

4. По катету и острому углу.

Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Теорема о сумме углов треугольника и следствия из нее.

1. Сумма внутренних углов треугольника равна 180 градусов.

2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.

3. Сумма внутренних углов выпуклого n-угольника равна 180(n-2).

4. Сумма внешних углов n-угольника равна 360 градусов.

5. Угол между биссектрисами смежных углов равен 90.

6. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.

Видео:Длина медианы треугольникаСкачать

Неравенство треугольника и следствия из него.

1. Сумма двух сторон треугольника больше его третьей стороны.

2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.

3. Против большего угла треугольника лежит большая сторона.

4. Против большей стороны треугольника лежит больший угол.

5. Гипотенуза прямоугольного треугольника больше катета.

6. Если из одной точки проведены к прямой перпендикуляр м наклонные, то

1)перпендикуляр короче наклонных

2) большей наклонной соответствует большая проекция и наоборот.

Видео:Формула медианы треугольникаСкачать

Средняя линия треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

Средняя линия треугольника параллельна стороне треугольника и равна ее половине.

Видео:Все факты о медиане треугольника для ЕГЭСкачать

Теоремы о медианах треугольника

1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.

2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный.

3. Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.

Видео:длина медианы #SHORTSСкачать

Свойство серединных перпендикуляров к сторонам треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.

Видео:Формулы для медианы треугольникаСкачать

Теорема о высотах треугольника

Прямые, содержащие высоты треугольника, пересекаются в одной точке.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Теорема о биссектрисах треугольника

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

Видео:Теорема о медианах треугольникаСкачать

Свойство биссектрисы треугольника

Биссектриса треугольника делит его сторону на отрезки пропорциональные двум другим сторонам.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки подобия треугольников

1. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то треугольники подобны.

3. Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то треугольники подобны.

Видео:Теорема о медианах треугольника.Скачать

Площади подобных треугольников

1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.

Видео:Теорема Стюарта | формулы для биссектрисы треугольника и медианыСкачать

В прямоугольном треугольнике

1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или косинус прилежащего к этому катету острого угла.

2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или котангенс прилежащего к этому катету острого угла.

3. Катет прямоугольного треугольника, лежащий против угла 30 градусов, равен половине гипотенузы.

4. R=c:2; r=(a+b-c):2=p-с, где a,b-катеты, а с-гипотенуза; R-радиус описанной окружности, r- радиус вписанной окружности, p- полупериметр.

Видео:11 класс, 45 урок, Теорема о медианеСкачать

Средние пропорциональные в прямоугольном треугольнике

Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Метрические соотношения в треугольнике

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Следствие из теоремы косинусов

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов.

Обобщенная теорема синусов

Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.

🎬 Видео

Урок 33. Свойство медиан треугольника (8 класс)Скачать