Как вычислить угол между вектором и осью

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Видео:Построение проекции вектора на осьСкачать

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

1. Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

1. Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Видео:Угол между векторами. 9 класс.Скачать

Лекция Применение векторов для вычисления величин углов и расстояний

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Угол между векторами | МатематикаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

ТЕМА 7.4 УГОЛ МЕЖДУ ВЕКТОРАМИ. УГОЛ МЕЖДУ ВЕКТОРОМ И ОСЬЮ

Содержание учебного материала:

Применение векторов для вычисления величин углов и расстояний:

1.Понятие угла между векторами.

2.Формула вычисления угла между векторами.

3.Понятие направляющих косинусов вектора.

4.Формулы вычисления направляющих косинусов вектора.

1.Понятие угла между векторами.

Угол между векторами — это угол между их направлениями (рис.1).

Угол между сонаправленными векторами равен 0.

Угол между противоположно направленными векторами равен

Угол между ортогональными векторами равен.

2. Формула вычисления угла между векторами.

Из определения скалярного произведения векторов находим угол

Пример 1. Найдите угол АСВ в треугольнике АВС, если, В(-2;0;7) и

Решение. 1. Угол АСВ в треугольнике АВС находится между векторами

и Определим координаты векторов:.

2. Найдём угол между векторами и по формуле (1) , подставив в неё соответствующие координаты:

3. Определим величину искомого угла по таблице значений тригонометрических функций или с помощью калькулятора:

Итак, угол между векторами и найден: .

3.Понятие направляющих косинусов вектора.

4.Формулы вычисления направляющих косинусов вектора.

Определим углы, составляемые вектором AB = (x; y; z) с координатными осями:

Пример 2 . Найти углы, составляемые вектором с координатными осями, если

1. Найдём координаты вектора:

2.Вычислим длину вектора:

3. Определим углы, составляемые вектором с координатными осями:

Итак, углы, составляемые вектором с координатными осями, равны

Краткое описание документа:

Содержание учебного материала:

Применение векторов для вычисления величин углов и расстояний:

1.Понятие угла между векторами в пространстве.

2.Формула вычисления угла между векторами в пространстве.

3.Понятие направляющих косинусов вектора в пространстве.

4.Формулы вычисления направляющих косинусов вектора.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 954 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 684 человека из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 67 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Как находить угол между векторамиСкачать

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 503 239 материалов в базе

Материал подходит для УМК

«Геометрия. Базовый и углубленный уровни», Нелин Е.П., Лазарев В.А.

§ 27. Применение метода координат и векторов к решению стереометрических задач

Другие материалы

• 09.06.2018
• 1260
• 10

• 09.06.2018
• 5276
• 147

• 09.06.2018
• 695
• 31

• 09.05.2018
• 1062
• 0

• 09.04.2018
• 754
• 1

• 03.04.2018
• 2193
• 3

• 28.02.2018
• 185
• 0

• 09.02.2018
• 5771
• 72

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 09.06.2018 690
• DOCX 85.6 кбайт
• 6 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Карсакова Елена Николаевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 7 лет и 11 месяцев
• Подписчики: 26
• Всего просмотров: 60335
• Всего материалов: 33

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Петербурге введут новые COVID-ограничения для несовершеннолетних

Время чтения: 2 минуты

Большинство российских школьников недовольны качеством питания в столовых

Время чтения: 1 минута

В Госдуме предложили доплачивать учителям за работу в классах, где выявлен ковид

Время чтения: 1 минута

Санкт-Петербургский госуниверситет переходит на дистанционное обучение

Время чтения: 1 минута

В Сыктывкаре школьников переведут на дистанционное обучение

Время чтения: 1 минута

Минобрнауки запускает конкурс студенческих научных обществ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Как вычислить угол между вектором и осью

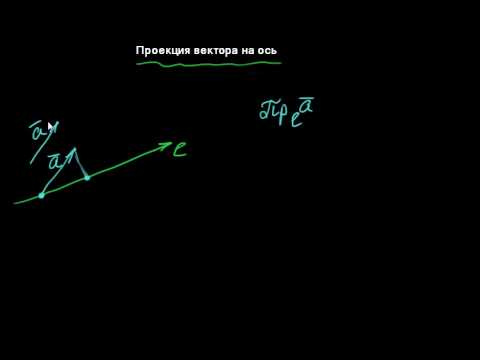
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).

Проекция вектора на ось обозначается через a_l или , а угол между осью и вектором будем обозначать так: . Таким образом,

(2)

Если — углы, образованные вектором с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора на координатные оси будут равны

(3)

В дальнейшем предполагается, что система координат — прямоугольная.

Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле

(4)

т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.

Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).

🎥 Видео

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Векторные величины Проекция вектора на осьСкачать

Анализ ЭКГ. Определение ЭОС- электрической оси сердца. (для студентов)Скачать

Угол между прямыми в пространстве. 10 класс.Скачать

§4 Проекция вектора на осьСкачать

найти угол между единичными векторамиСкачать

Проекция вектора на вектор.Скачать

100 Угол между векторамиСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Нахождение угла между векторами через координаты. 9 класс.Скачать

Основы кинематики. Тема 3. Проекция вектора на осьСкачать