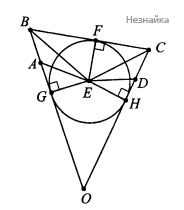
В пятиугольнике abcde вписан в окружность (4 видео)

В пятиугольнике abcde вписан в окружность

Пятиугольник ABCDE вписан в окружность. Из вершины A опущены перпендикуляры AF, AH, AP и AQ на прямые DE, BE, CD и BC соответственно.

а) Докажите, что

б) Найдите AH, если и

а) Мы будем пока считать, что F и Q лежат на продолжениях DE и CB соответственно а остальные точки — на отрезках. Тогда четырехугольники FEHA и APCQ вписанные (имеют по два противоположных прямых угла), откуда

что и требовалось.

Пусть теперь Q лежит на продолжении CB, а остальные точки — на отрезках. Тогда четырехугольники FEHA и APCQ вписанные (имеют два противоположных прямых угла второй идва равных прямых угла между стороной и диагональю первый), откуда что и требовалось.

Аналогично разбираются остальные случаи расположения точек.

б) Углы QCA и HEA равны как вписанные углы, опирающиеся на одну дугу AB, поэтому прямоугольные треугольники CQA и AHE подобны. Углы AEF и ACP равны, так как оба они в сумме с углом AED дают 180°. Следовательно, подобны прямоугольные треугольники AFE и APC. Тогда верны пропорции и Разделим первую на вторую, получим откуда

Ответ:

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)	3
Получен обоснованный ответ в пункте б) имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки	2
Имеется верное доказательство утверждения пункта а) при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, Содержание Пятиугольник ABCDE вписан в окружность, его диагональ AC параллельна стороне ED. Сравните периметры четырехугольников EABC и DCBA. Ваш ответ Похожие вопросы В пятиугольнике abcde вписан в окружность 🌟 Видео Видео:ЕГЭ задание 16 Пятиугольник вписан в окружностьСкачать Пятиугольник ABCDE вписан в окружность, его диагональ AC параллельна стороне ED. Сравните периметры четырехугольников EABC и DCBA. Видео:Четырёхугольник ABCD вписан в окружность ... 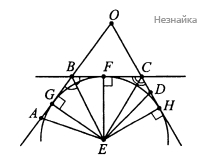\| ОГЭ 2017 \| ЗАДАНИЕ 10 \| ШКОЛА ПИФАГОРАСкачать Ваш ответ Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать Похожие вопросы Все категории экономические 43,277 гуманитарные 33,618 юридические 17,900 школьный раздел 606,921 разное 16,829 Популярное на сайте: Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так. Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. Видео:Построение пятиугольника циркулем и линейкойСкачать В пятиугольнике abcde вписан в окружность В выпуклом пятиугольнике ABCDE диагонали BE и СЕ являются биссектрисами неравных углов при вершинах В и С соответственно. а) Докажите, что точка Е есть центр вписанной или вневписанной окружности треугольника ОСВ, где О — точка пересечения прямых CD и АВ. б) Найдите площадь пятиугольника ABCDE, если ∠А = 37°, ∠D = 143°, а площадь треугольника ВСЕ равна 13. а) Пусть точки [math]O[/math] и [math]E[/math] расположены по одну сторону от прямой [math]BC[/math] (см. рисунок), то есть [math]angle B+angle C=180^circ[/math], тогда [math]BE[/math] и [math]CE[/math] являются биссектрисами внутренних углов при вершинах [math]B[/math] и [math]C[/math] соответственно треугольника [math]BCO[/math]. По свойству биссектрисы [math]BE[/math] точка [math]E[/math] равноудалена от сторон [math]BO[/math] и [math]BC[/math]. Аналогично по свойству биссектрисы [math]CE[/math] точка [math]E[/math] равноудалена от сторон [math]BC[/math] и [math]OC[/math]. Следовательно, точка [math]E[/math] равноудалена от всех сторон треугольника [math]BCO[/math] и является центром окружности, вписанной в этот треугольник. Рассмотрим другой случай. Пусть точки [math]O[/math] и [math]E[/math] расположены по разные стороны от прямой [math]BC[/math](см. рисунок ниже), то есть [math]angle B+angle C>180^circ[/math], тогда [math]BE[/math] и [math]CE[/math] являются биссектрисами внешних углов при вершинах [math]B[/math] и [math]C[/math] cсоответственно треугольника [math]BCO[/math]. По свойству биссектрисы [math]BE[/math] точка [math]E[/math] равноудалена от прямых [math]BO[/math] и [math]BC[/math]. Аналогично точка [math]E[/math] равноудалена от прямых [math]BC[/math] и [math]OC[/math]. Следовательно, точка [math]E[/math] равноудалена от стороны [math]BC[/math] и продолжений сторон [math]BO[/math] и [math]OC[/math] треугольника [math]BCO[/math] и является центром вневписанной окружности этого треугольника. [math]EG,EF,EH;-;[/math] радиусы этой окружности. б) Сумма углов выпуклого пятиугольника равна [math]540^circ[/math]. По условию задачи [math]angle A=37^circ,[/math][math]angle D=143^circ,[/math][math]angle A+angle D=180^circ[/math]. Если [math]angle B+angle C=180^circ,[/math], что противоречит условию выпуклости прямоугольника. Значит [math]angle B+angle C>180^circ,[/math], поэтому: [math]bigtriangleup AGE=bigtriangleup DHE[/math] по катету и острому углу. Аналогично [math]bigtriangleup EHC=bigtriangleup EFC.;[/math] Последовательно имеем: 🌟 Видео Четырехугольники, вписанные в окружность. 9 класс.Скачать Треугольник ABC вписан в окружность с центром O Угол BAC равен 32°Скачать ЕГЭ. Задача 16. Пятиугольник вписан в окружностьСкачать 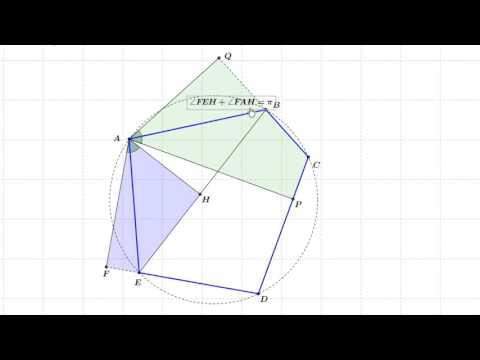✓ Степень точки в ЕГЭ \| Резерв досрока ЕГЭ-2022. Задание 16. Профильный уровень \| Борис ТрушинСкачать Правильные многоугольники. Геометрия 9 класс \| Математика \| TutorOnlineСкачать Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать №1.161. В выпуклом пятиугольнике ABCDE известно, что AE = AD, AC = AB и ∠DAC = ∠AEB+∠ABE. ДокажитеСкачать Вписанные и описанные окружности. Вебинар \| МатематикаСкачать Урок 2. Описанная окружность около четырехугольника. Задача из ОГЭ\| Подобные треугольникиСкачать Вписанный в окружность четырёхугольник.Скачать ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать #3warmup. Разбор третьей разминкиСкачать ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать Вписанная и описанная окружность - от bezbotvyСкачать Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать Вписанные четырехугольники. 9 класс.Скачать Поделиться или сохранить к себе: Search for: Треугольник Какое число прячется под треугольником Окружность При каком условии можно описать окружность 1312 Треугольник Все формулы треугольников для огэ 1322 Окружность Окружность описанная вокруг выпуклого четырехугольника 1312 Вектор Метод крылова собственные векторы 1313 Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности О сайте \| \| © 2024 Курс школьной геометрии.

Критерии оценивания выполнения задания

Баллы

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б)

Получен обоснованный ответ в пункте б)

имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)

при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,

Содержание

Пятиугольник ABCDE вписан в окружность, его диагональ AC параллельна стороне ED. Сравните периметры четырехугольников EABC и DCBA.
Ваш ответ
Похожие вопросы
В пятиугольнике abcde вписан в окружность
🌟 Видео

Видео:ЕГЭ задание 16 Пятиугольник вписан в окружностьСкачать

Пятиугольник ABCDE вписан в окружность, его диагональ AC параллельна стороне ED. Сравните периметры четырехугольников EABC и DCBA.

Видео:Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Ваш ответ

Видео:2041 четырёхугольник ABCD вписан в окружность угол abd равен 38 угол cаd равен 54 Найдите угол ABCСкачать

В пятиугольнике abcde вписан в окружность

В выпуклом пятиугольнике ABCDE диагонали BE и СЕ являются биссектрисами неравных углов при вершинах В и С соответственно.

а) Докажите, что точка Е есть центр вписанной или вневписанной окружности треугольника ОСВ, где О — точка пересечения прямых CD и АВ.

б) Найдите площадь пятиугольника ABCDE, если ∠А = 37°, ∠D = 143°, а площадь треугольника ВСЕ равна 13.

а) Пусть точки [math]O[/math] и [math]E[/math] расположены по одну сторону от прямой [math]BC[/math] (см. рисунок), то есть [math]angle B+angle C=180^circ[/math], тогда [math]BE[/math] и [math]CE[/math] являются биссектрисами внутренних углов при вершинах [math]B[/math] и [math]C[/math] соответственно треугольника [math]BCO[/math]. По свойству биссектрисы [math]BE[/math] точка [math]E[/math] равноудалена от сторон [math]BO[/math] и [math]BC[/math]. Аналогично по свойству биссектрисы [math]CE[/math] точка [math]E[/math] равноудалена от сторон [math]BC[/math] и [math]OC[/math]. Следовательно, точка [math]E[/math] равноудалена от всех сторон треугольника [math]BCO[/math] и является центром окружности, вписанной в этот треугольник.

Рассмотрим другой случай. Пусть точки [math]O[/math] и [math]E[/math] расположены по разные стороны от прямой [math]BC[/math](см. рисунок ниже), то есть [math]angle B+angle C>180^circ[/math], тогда [math]BE[/math] и [math]CE[/math] являются биссектрисами внешних углов при вершинах [math]B[/math] и [math]C[/math] cсоответственно треугольника [math]BCO[/math]. По свойству биссектрисы [math]BE[/math] точка [math]E[/math] равноудалена от прямых [math]BO[/math] и [math]BC[/math]. Аналогично точка [math]E[/math] равноудалена от прямых [math]BC[/math] и [math]OC[/math]. Следовательно, точка [math]E[/math] равноудалена от стороны [math]BC[/math] и продолжений сторон [math]BO[/math] и [math]OC[/math] треугольника [math]BCO[/math] и является центром вневписанной окружности этого треугольника. [math]EG,EF,EH;-;[/math] радиусы этой окружности.

б) Сумма углов выпуклого пятиугольника равна [math]540^circ[/math]. По условию задачи [math]angle A=37^circ,[/math][math]angle D=143^circ,[/math][math]angle A+angle D=180^circ[/math]. Если [math]angle B+angle C=180^circ,[/math], что противоречит условию выпуклости прямоугольника. Значит [math]angle B+angle C>180^circ,[/math], поэтому: [math]bigtriangleup AGE=bigtriangleup DHE[/math] по катету и острому углу. Аналогично [math]bigtriangleup EHC=bigtriangleup EFC.;[/math] Последовательно имеем: