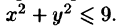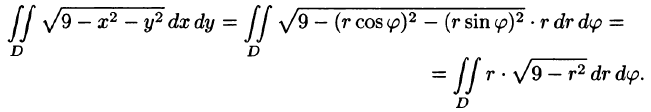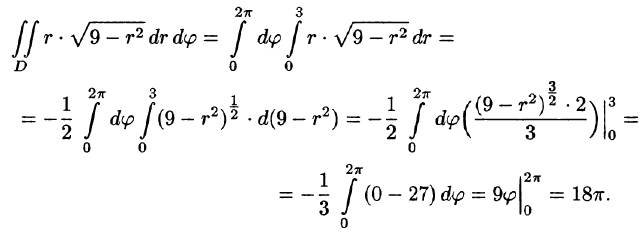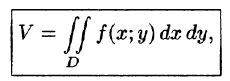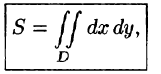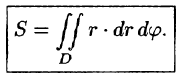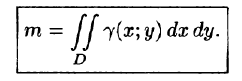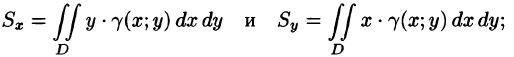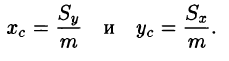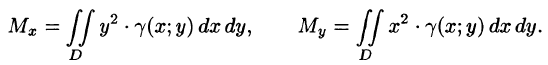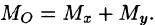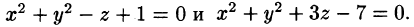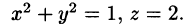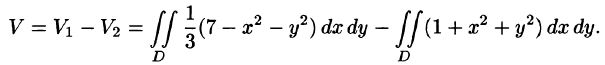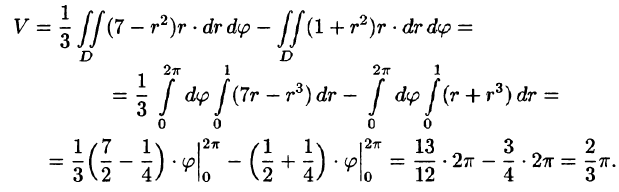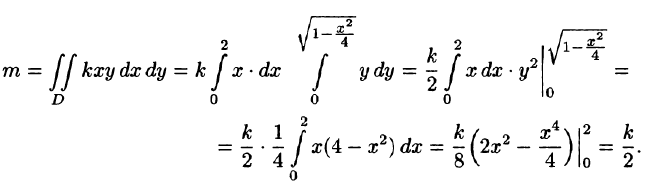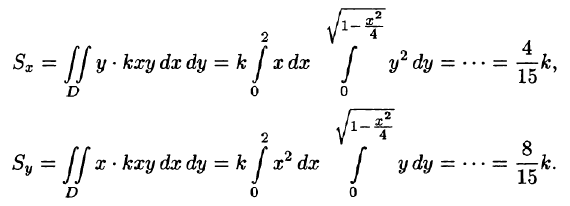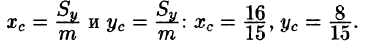- Что значит вычислить двойной интеграл в полярных координатах?
- Пределы интегрирования в повторных интегралах
- Случай первый
- Случай второй
- Случай третий
- Случай четвёртый
- Решения двойных интегралов в полярных координатах: примеры
- Двойной интеграл с примерами решения и образцами выполнения
- Геометрический и физический смысл двойного интеграла
- Масса плоской пластинки
- Основные свойства двойного интеграла
- Вычисление двойного интеграла в декартовых координатах
- Вычисление двойного интеграла в полярных координатах
- Приложения двойного интеграла
- Объем тела
- Площадь плоской фигуры
- Масса плоской фигуры
- Статические моменты и координаты центра тяжести плоской фигуры
- Моменты инерции плоской фигуры
- Двойной интеграл
- Примеры решений двойных интегралов
- Порядок интегрирования: примеры решений
- Двойной интеграл по области: примеры решений
- Площади: примеры решений
- Объемы: примеры решений
- Масса, центр тяжести, момент: примеры решений
- 💥 Видео
Видео:Двойной интеграл в полярных координатахСкачать

Что значит вычислить двойной интеграл в полярных координатах?
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

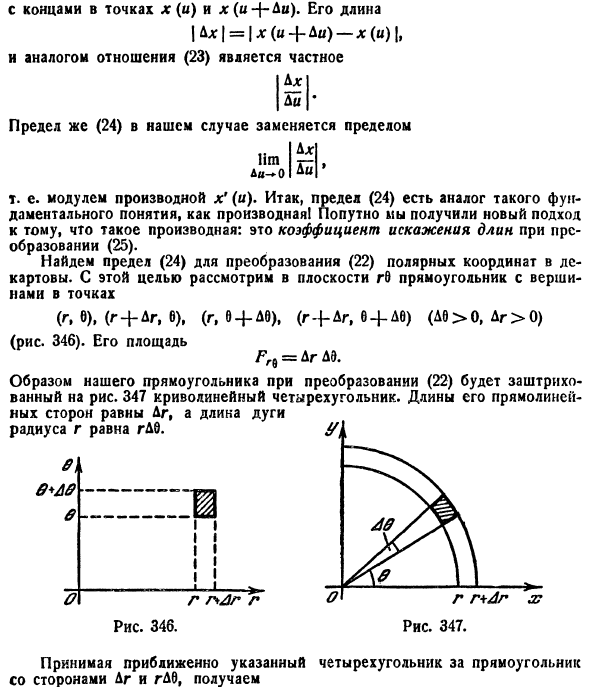
Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:
а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .
Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать
Пределы интегрирования в повторных интегралах
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый
Полюс O находится вне области интегрирования D .
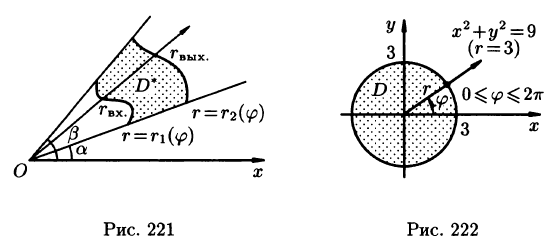
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Решения двойных интегралов в полярных координатах: примеры
Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 


Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.
Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
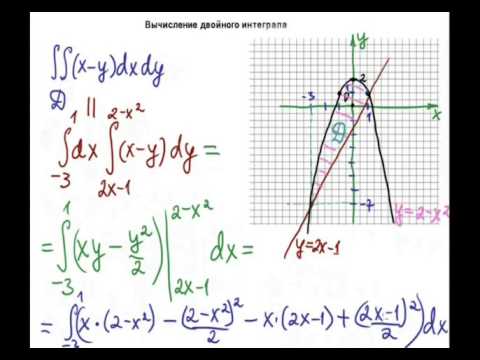
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет 




Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : 

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:
Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности 
Решение. Строим на чертеже область интегрирования.
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности 




Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:
В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:
Пример 4. Вычислить плоской фигуры, которую ограничивают линии 



Решение. Построим заданную фигуру на следующем рисунке.
Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:
Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:
Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:
Видео:Вычислить двойной интеграл, перейдя к полярным координатамСкачать

Двойной интеграл с примерами решения и образцами выполнения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
Пусть в замкнутой облас
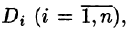

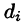
В каждой области 
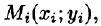
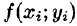

Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 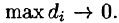
Таким образом, двойной интеграл определяется равенством
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
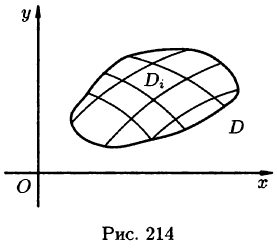
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
равенство (53.2) можно записать в виде
Видео:Математика без ху!ни. Двойные интегралы. Часть1. Как вычислять.Скачать

Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
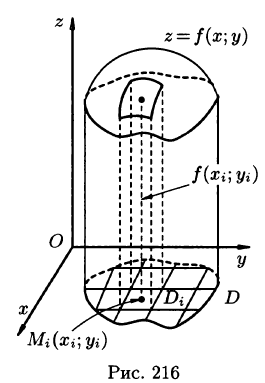
Рассмотрим тело, ограниченное сверху поверхностью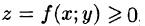

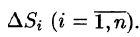

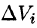
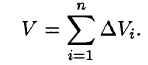
Возьмем на каждой площадке Di произвольную точку 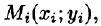

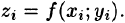
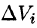
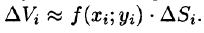
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей» 

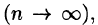
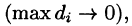
или, согласно равенству (53.2),
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 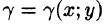
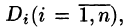


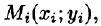
Если области D, достаточно малы, то плотность в каждой точке 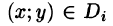
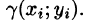

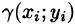
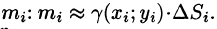
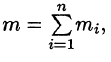
Точное значение массы получим как предел суммы (53.5) при условии
или, согласно равенству (53.2),
Итак, двойной интеграл от функции 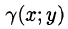
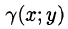
Видео:Математический анализ, 41 урок, Вычисление двойных интеграловСкачать

Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
3.Если область D разбить линией на две области 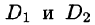
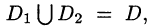
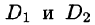
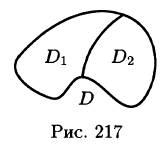
4.Если в области D имеет место неравенство 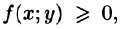
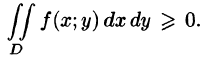
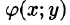
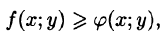
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 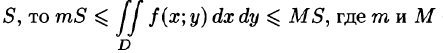
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка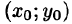
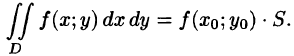
называют средним значением функции f(x; у) в области D.
Видео:Вычислить двойной интегралСкачать

Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 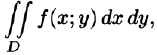
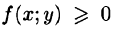
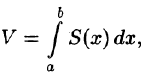
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
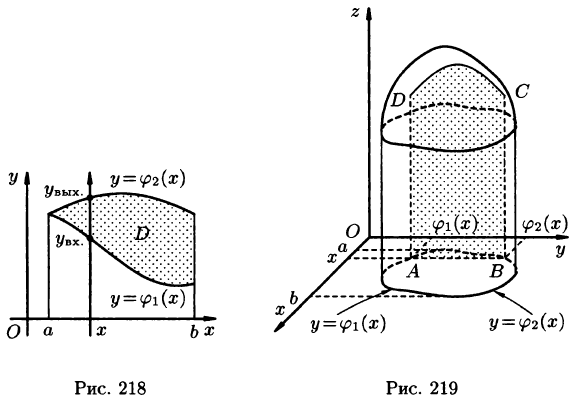
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми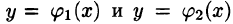
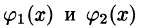
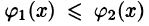
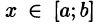
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
Площадь S(x) этой трапеции находим с помощью определенного интеграла
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 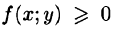
Это равенство обычно записывается в виде
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 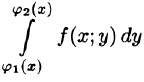
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 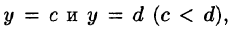
для всех 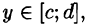
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении осиОх или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 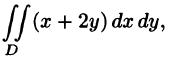
Решение:
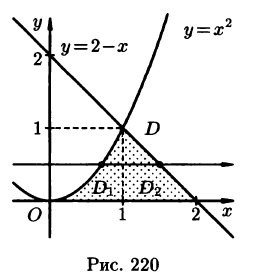
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
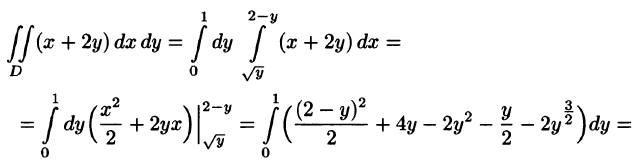
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 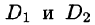
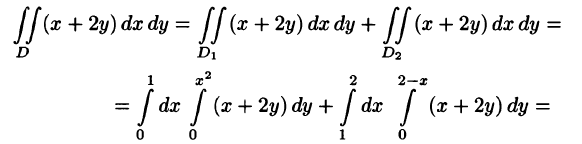
Ответ, разумеется, один и тот же.
Видео:Математика без ху!ни. Двойной интеграл, вычисление двумя способами.Скачать
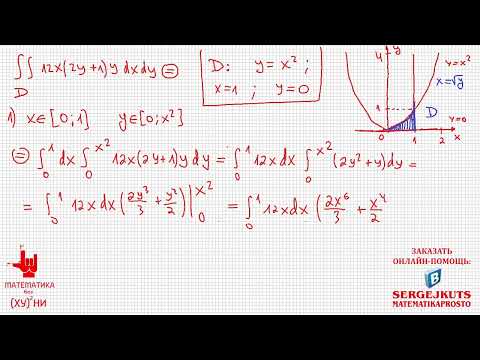
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами
В качестве инь возьмем полярные координаты 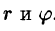
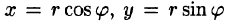
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
Формула замены переменных (53.11) принимает вид:
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами 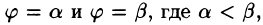
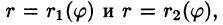
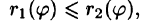
Внутренний интеграл берется при постоянном
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
область Dесть круг, кольцо или часть таковых.
- На практике переход к полярным координатам осуществляется путем замены
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
(исследуя закон изменения
точки
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 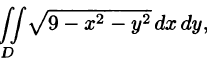
Решение: Применив формулу (53.12), перейдем к полярным координатам:
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 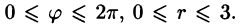
Видео:Вычисление двойного интегралаСкачать
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 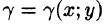
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
а координаты центра масс фигуры по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 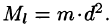
Момент инерции фигуры относительно начала координат — по формуле
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
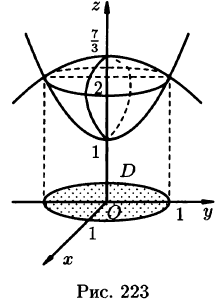
Найти объем тела, ограниченного поверхностями
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
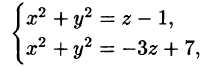
находим уравнение линии их пересечения:
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 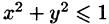
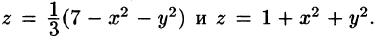
Переходя к полярным координатам, находим:
Пример:
Найти массу, статические моменты 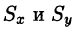
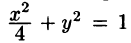
Решение: По формуле (53.6) находим массу пластинки. По условию, 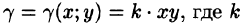
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
Видео:Вычислить двойной интегралСкачать

Двойной интеграл













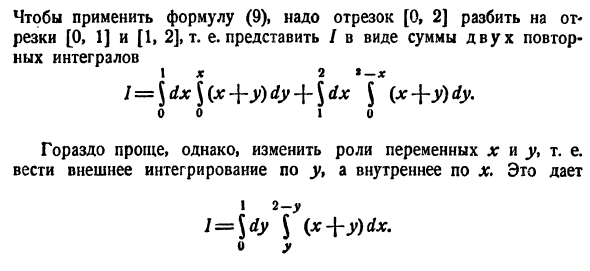


















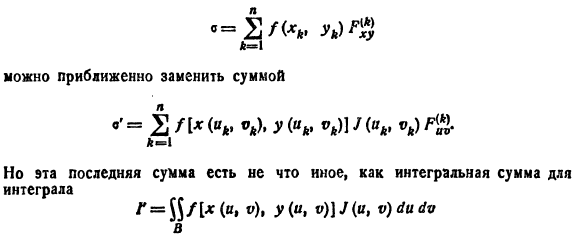




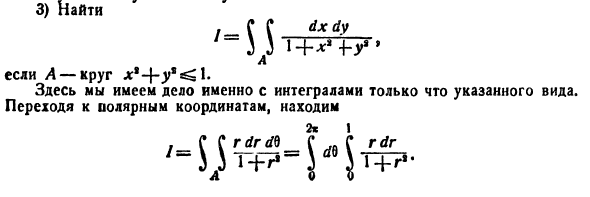




Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Двойной интеграл (ч.25). Вычисление в полярных координатах. Высшая математика.Скачать

Примеры решений двойных интегралов
В этом разделе вы найдете подробные решения заданий с использованием двойных интегралов разной сложности. Для удобства использования примеры разбиты по подразделам:
Видео:Вычислить двойной интеграл ★ Замена переменных в двойном интегралеСкачать

Порядок интегрирования: примеры решений
Задача 1. Изменить порядок интегрирования.
$$ int_0^1 dy int_<-sqrt>^0 fdx +int_1^e dy int_^<ln> fdx $$
Задача 2. Свести к однократному интегралу
Задача 3. Изменить порядок интегрирования. Нарисовать область интегрирования и вычислить двойной интеграл двумя способами.
Трудности с задачами? МатБюро поможет с интегралами.
Видео:Двойные интегралы в полярных координатахСкачать

Двойной интеграл по области: примеры решений
Задача 4. Вычислить двойной интеграл по области $D$
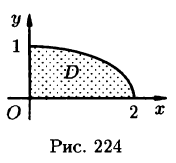
Задача 5. Вычислить двойной интеграл от функции $z=x^3+y^3-3xy$ по области D, заданной системой неравенств $0 le x le 2$, $y le sqrt$. Область D изобразить на рисунке.
Задача 6. Вычислить с помощью перехода к полярным координатам двойной интеграл по указанной области $D$.
Видео:Объем через двойной интегралСкачать
Площади: примеры решений
Задача 7. Вычислить площадь области D: $y=-2x^2+2, y ge -6$.
Задача 8. Найти площадь области $x^2-2x+y^2=0$, $x^2-4x+y^2=0$, $y=0$, $y=sqrtx$.
Задача 9. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями (неравенствами) $y=x^2,x=2y^2$
Задача 10. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной заданными линиями.
Задача 11. Вычислить площадь области, заданной неравенствами $(x-r)^2+y^2 le r^2, y ge 0, -2x+2r ge y$, перейдя предварительно к полярным координатам.
Если вам нужна помощь в нахождении интегралов, выполнении домашней работы или типовика по интегральному исчислению, будем рады принять ваш заказ на решение. Стоимость от 60 рублей, срок от нескольких часов.
Видео:Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Объемы: примеры решений
Задача 12. Найти объем тела, заданного ограничивающими его поверхностями.
$$ x^2+y^2=2y, quad x^2+y^2=5y, quad z=sqrt, quad z=0. $$
Задача 13. С помощью двойного интеграла вычислить объем тела, ограниченного поверхностями
$$ a^2 le x^2+y^2 le b^2, quad x^2-y^2-z^2 ge 0, xge 0$$
Задача 14. Вычислить объем тела, ограниченного поверхностями, с помощью двойного и тройного интеграла $x^2+y^2=4x,x^2+y^2+z^2=16$
Видео:Площадь круга через интегралСкачать

Масса, центр тяжести, момент: примеры решений
Задача 15. Пластина $D$ задана уравнениями $x=1$, $y ge 0$, $y^2=4x$ с плотностью $mu = 6x+3y^2$. Найти массу пластины.
Задача 16. Найти координаты центра тяжести однородной пластины, ограниченной кривой
$$ x=a(t-sin t), y=a(1-cos t), quad 0 le t le 2pi; y=0. $$
Задача 17. Найти центр тяжести плоской пластины, ограниченной кривой $(x+y)^4=xy$, имеющей плотность
Задача 18. Используя двойной интеграл, вычислить статический момент относительно оси $Ox$ тонкой однородной пластинки, имеющей форму области $D$, ограниченной заданными линиями. Построить чертеж области интегрирования
Задача 19. Найти массу круглой пластины $D: x^2+y^2 le 1$ с поверхностной плотностью $rho(x,y)=3-x-y$.
Задача 20. Найти момент инерции относительно оси $Ox$ однородной фигуры, ограниченной двумя кривыми $y^2=8x+4$, $y^2=-8x+4$.
💥 Видео
Изменение порядка интегрирования в повторном интегралеСкачать

Вычислить двойной интеграл по областиСкачать






















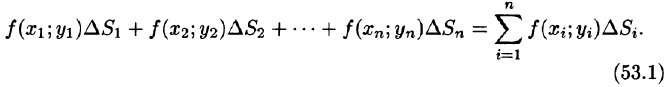
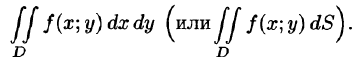
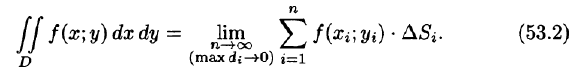
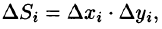 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде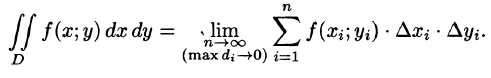
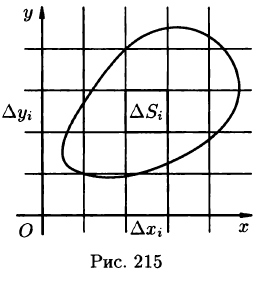

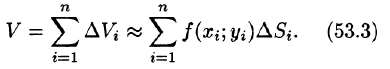
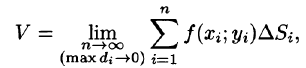
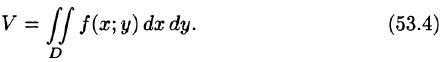
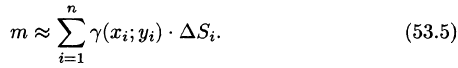
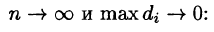
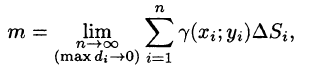
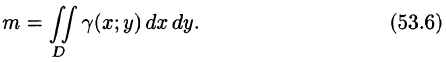
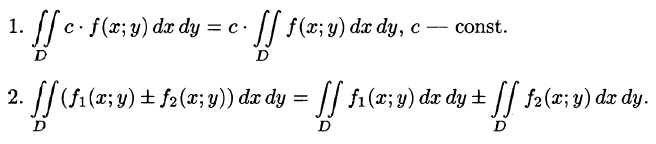
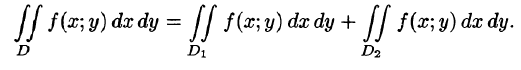
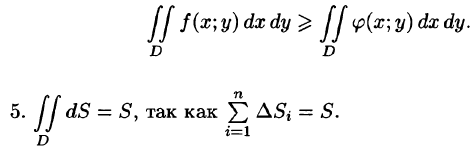
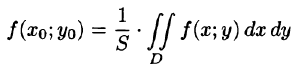
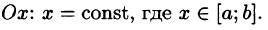
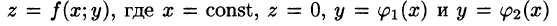
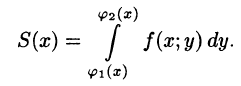
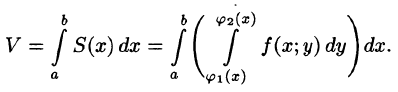
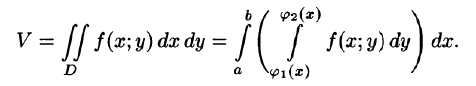
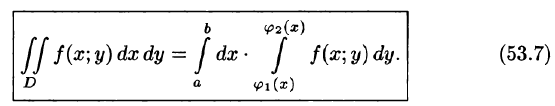
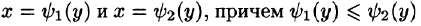
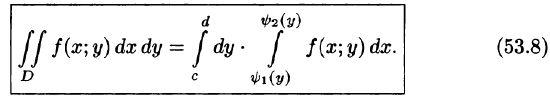
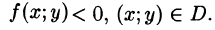
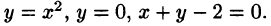
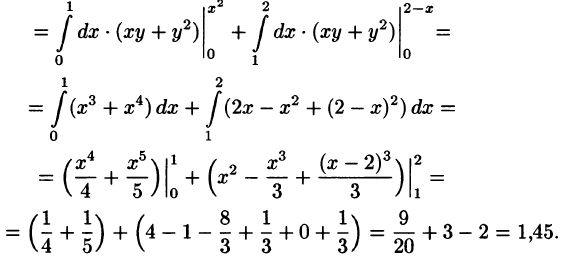
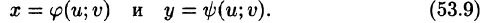

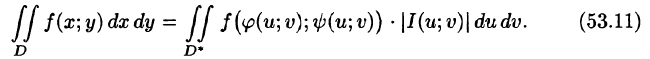
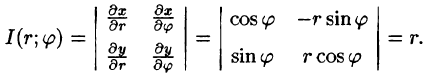
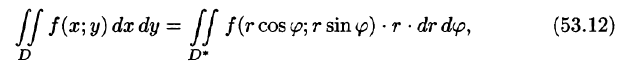
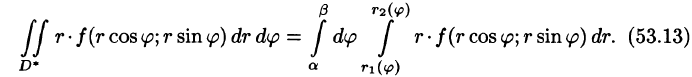
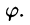
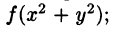 область Dесть круг, кольцо или часть таковых.
область Dесть круг, кольцо или часть таковых.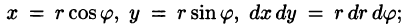 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по 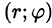 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).