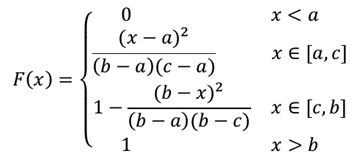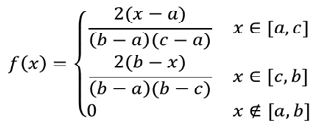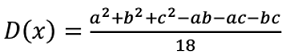Функция в виде треугольника (7 видео) | Курс школьной геометрии

Определение функций формы линейного треугольного элемента

Пусть известна функция перемещений и(у, z) вдоль какой-либо оси. На рис. 23.3 показана поверхность перемещений, построенная перпендикулярно поверхности рассматриваемого плоского тела. Функции формы определяют способ аппроксимации искомой функции (в нашем случае поверхности перемещений).

Рис. 23.3. Аппроксимация поверхности перемещений плоскими треугольниками

Разобьем тело на плоские треугольные элементы. Выделим один из элементов (на рисунке заштрихован). В узлах 1, 2, 3 элемента известны перемещения А,, Д₂, Д₃. Требуется найти перемещение и(у, z) в некоторой произвольной точке между узлами.

Сначала определяют узловые перемещения. Следовательно, поверхности перемещений еще нет, а есть дискретный набор перемещений в узлах. Необходимо выбрать форму аппроксимации перемещений между узлами. Для этой цели и используются функции формы

Через три точки поверхности (А,, Д₂, Д₃) однозначно можно провести только плоскость. Для построения криволинейной поверхности трех точек недостаточно и надо выбирать вид элемента с большим количеством узлов.

Итак, для треугольного элемента выбираем плоскость как вид аппроксимации поверхности перемещений. По уравнению (22.1) перемещение и в произвольной точке связано с узловыми перемещениями А с помощью функций формы N.

Рассмотрим перемещение произвольной точки с координатами z и у вдоль оси zu_z = N|А, + N₂A₂ + 7V₃A₃.

Функции формы запишем как уравнение плоскости N = ау + bz = с. Значения коэффициентов а, b, с найдем из граничных условий. Для функции формы Nj в узле 1 Nj = 1, в узлах 2 и 3 >Vj = О, тогда

Решая эту систему уравнений, находим коэффициенты a_h b_h Cj Аналогично определяем коэффициенты для функций формы N₂ и N₃. В общем виде выражение для функций формы можно записать так:

Вывод: функция формы зависит только от координат узла элемента.

Для упорядочения расчетов примем правило нумерации узлов перемещений и функций формы.

Нумерация узлов элемента осуществляется против часовой стрелки. Начало нумерации (узел 1) — нижний левый (рис. 23.4). Горизонтальные перемещения (вдоль оси z) —нечетные, вертикальные перемещения (вдоль оси у) — четные.

Рис. 23.4. Примеры нумерации узлов и перемещений треугольного элемента

Содержание

Что нам стоит полином Жегалкина построить…
Метод треугольника Паскаля
Функция треугольного закона распределения симпсона имеет вид
🔍 Видео

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Что нам стоит полином Жегалкина построить…

Думаю, каждый, кто изучал или изучает в университете дискретную математику, знаком с понятием многочлена Жегалкина.

Главная особенность этих многочленов состоит в том, что любую булеву функцию можно представить полиномом Жегалкина, причем единственным образом.

Чаще всего для построения полиномов Жегалкина студентам предлагаются два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований.

Расчеты с использованием данных методов часто оказываются громоздкими. По невнимательности допустить ошибку не составляет труда.

Под катом приведен один удобный алгоритм, для построения полиномов Жегалкина, который студенты воспринимают «на ура», т.к. требует только выполнение «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но на мой взгляд по нему не совсем понятно, как быстро проводить вычисления. Мне метод известен под названием «метод треугольника Паскаля».

Порядок проведения вычислений проще показать на примере. Далее я буду по шагам показывать, как должен выглядеть расчет на бумаге (или как его удобно проводить).

Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Метод треугольника Паскаля

Требуется построить полином Жегалкина для функции f. Для примера, в качестве функции f возьмем функцию голосования .

Шаг 1. Строим таблицу значений функции (строки в таблице идут в порядке возрастания двоичных кодов). Таблицу лучше разместить в левой части листа.

Шаг 2. Построение треугольника.

Для этого берем вектор значения функции и выписываем его напротив первой строки таблицы:

Далее заполняем треугольник, складывая попарно соседние значения по модулю 2, результат сложения выписываем ниже.

Продолжаем вычисления, пока в строке не останется лишь одна цифра.

Шаг 3. Построение полинома Жегалкина.

Нас интересует левая сторона треугольника (значения выделены жирным):

Числа на левой стороне (выделены жирным шрифтом) треугольника есть коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных.

Теперь выпишем для наглядности эти конъюнкции. Конъюнкции выписываем по двоичным наборам в левой части таблицы по следующему принципу: если напротив переменной xi стоит 1, то переменная входит в конъюнкцию; в противном случае переменная отсутствует в конъюнкции. Набору (0,0,0) соответствует константа 1.

Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома.

Для построения полинома нужны только конъюнкции из строк с единицами на левой стороне треугольника.

Это и есть конъюнкции, входящие в состав полинома Жегалкина. Осталось лишь выписать сам полином:

Если переменных в функции не 3, а 4 или больше, то метод работает без изменений, только увеличатся размеры таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно без особых усилий выполнить на листе бумаги.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Функция треугольного закона распределения симпсона имеет вид

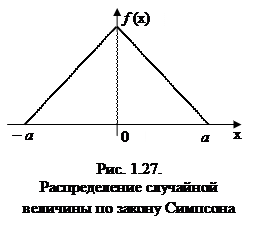К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника (рис. 1.27), из-за чего закон Симпсона часто называют законом треугольника.

При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид:

, (1.63)

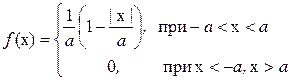
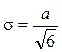
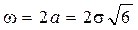
M_x = 0 , , . (1.64)

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9137 – | 7300 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Функция треугольного распределения случайной величины определяется формулой:

Плотность треугольного распределения СВ находится по формуле:

Математическое ожидание — формула:

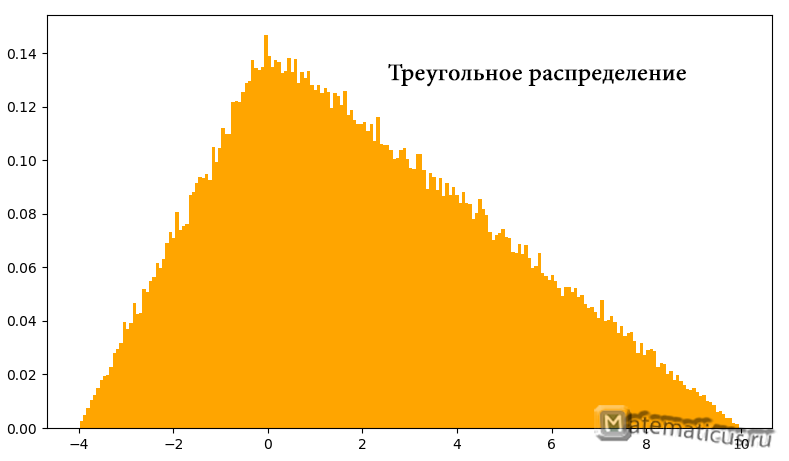
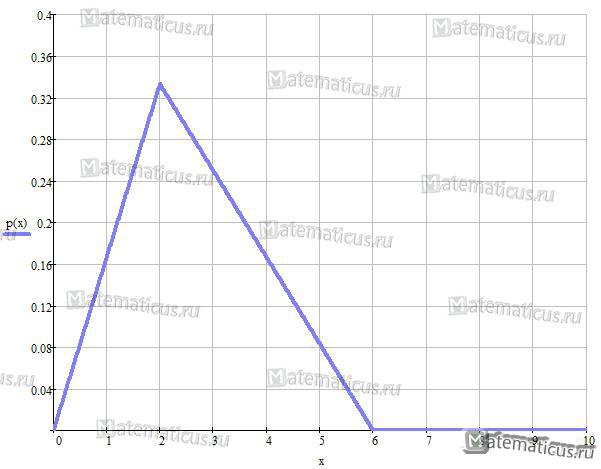
График плотности треугольного распределения случайной величины в диапазоне от -4 до 10

График плотности треугольного распределения случайной величины

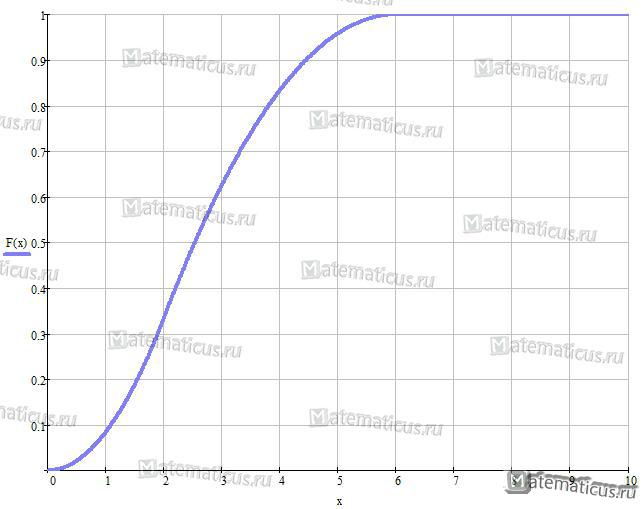
График функции треугольного распределения случайной величины

Треугольное распределения является приблизительной моделью и применяется, когда недостаточно данных или они отсутствуют. Треугольный закон распределения также используется для построения сложных законов распределения.

Он характерен для случайных погрешностей цифровых приборов, в которых измеряемая величина преобразуется в пропорциональный интервал времени Т_сч, называемый временем счета, а измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих период следования Т . В связи со случайным положением счетных импульсов относительно интервала Т_сч, а также случайным соотношением между периодом Т и временем счета Т_сч треугольный закон представляет собой композицию (объединение) двух равномерных законов с одинаковыми по величине максимальными погрешностями.

Функция распределения одномерной плотности вероятности случайных погрешностей для треугольного закона задается следующими соотношениями: