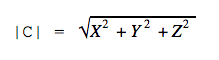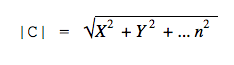Как сложить и перемножить векторы (и зачем).
Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.
Напомним основные мысли:
- Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
- В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
- Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
- Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.
С векторами можно совершать некоторые математические операции. Вот о них и поговорим.
- Правильно — векторы
- Сложение
- Интуитивное изображение сложения
- Вычитание
- Длина вектора
- Умножение и деление вектора на число
- Да вроде несложно!
- Что дальше
- Вычитание векторов
- Вектор
- Особые случаи векторов
- Вычитание векторов
- Что мы узнали?
- Сумма и разность векторов
- Сумма векторов
- Формула сложения векторов
- Свойства сложения векторов
- Разность векторов
- Формула вычитания векторов
- Примеры задач
- 📺 Видео
Видео:➡️ КАК ВЫЧИТАТЬ ВЕКТОРЫ?Скачать

Правильно — векторы
Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сложение
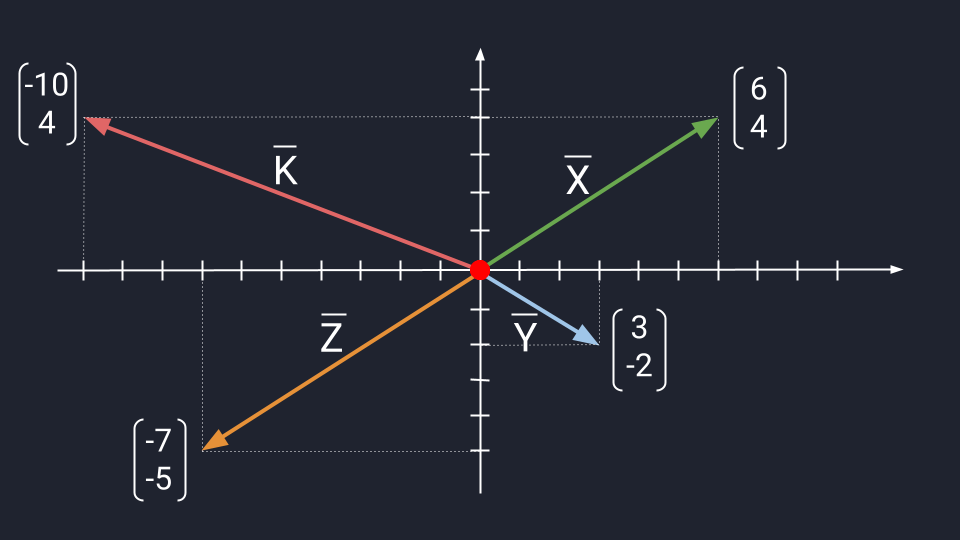
Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.
Предположим, нам нужно сложить векторы X и Y.
X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)
Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.
Например, вот сложение векторов с пятью координатами:
X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)
Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.
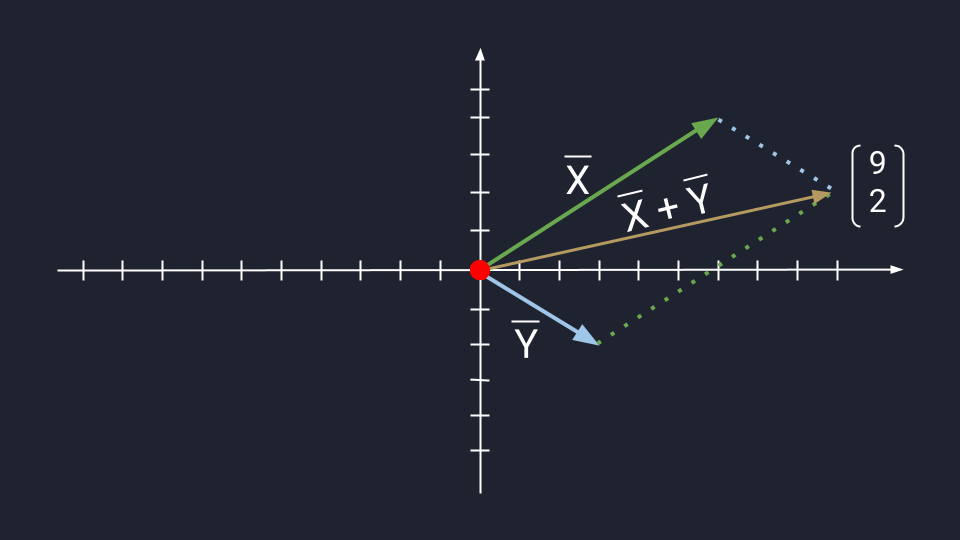
Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.
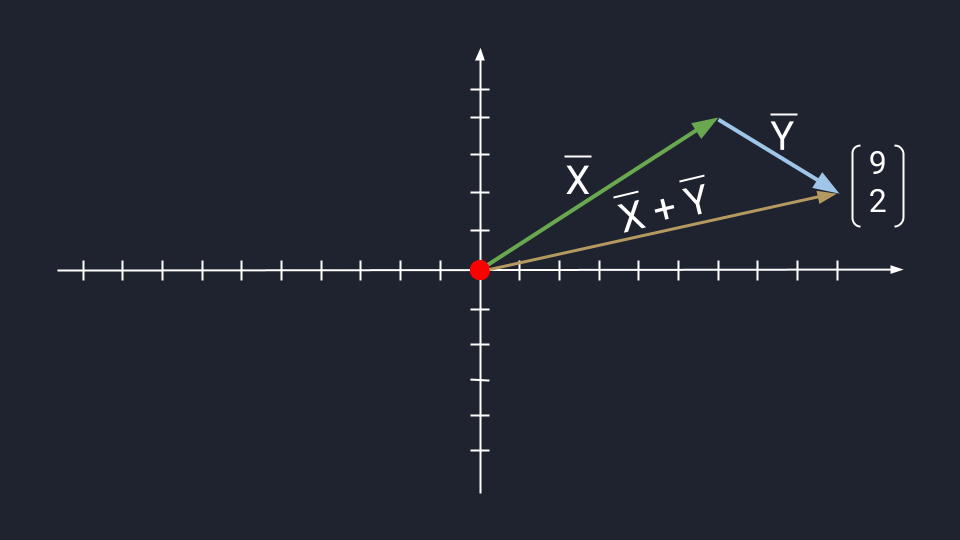
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.
Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.
Видео:Коллинеарность векторовСкачать

Вычитание
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)
Дальше используются правила сложения. Пошагово это выглядит так:
- У нас есть X = (6, 4) и Y = (3, −2).
- Превращаем формулу Х − Y в формулу Х + (−Y).
- Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
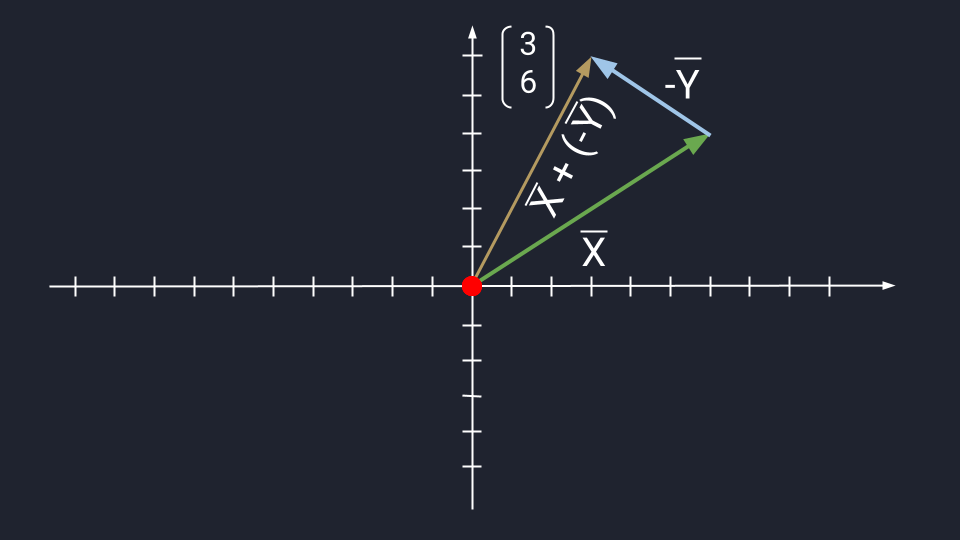
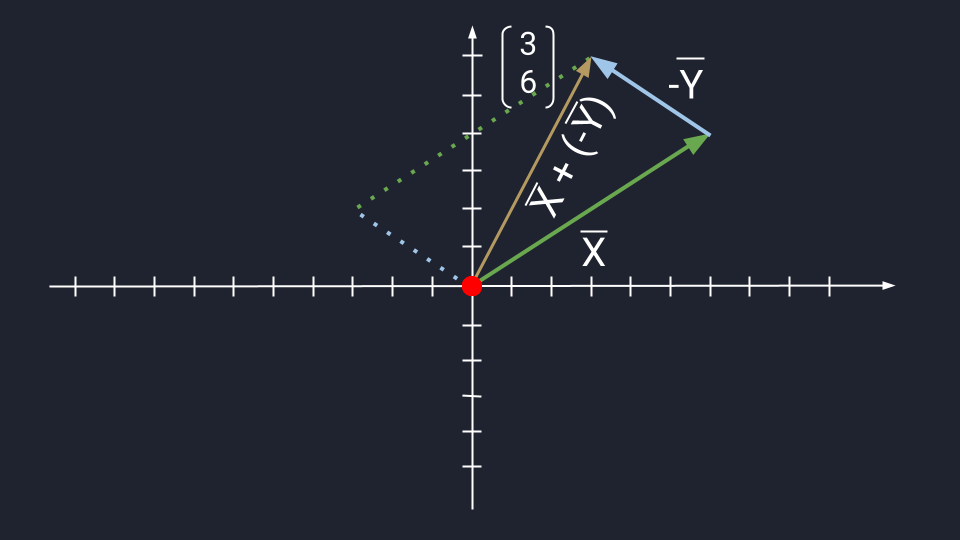
- Считаем: X + (−Y) = (3, 6).
Теперь посмотрим, как выглядит вычитание векторов на графике:
Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Длина вектора
Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.
Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:
X = 6 − 2 = 4
Y = 5 − 2 = 3
Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:
|C|2 = 42 + 32 = 25
|C| = √25 = 5 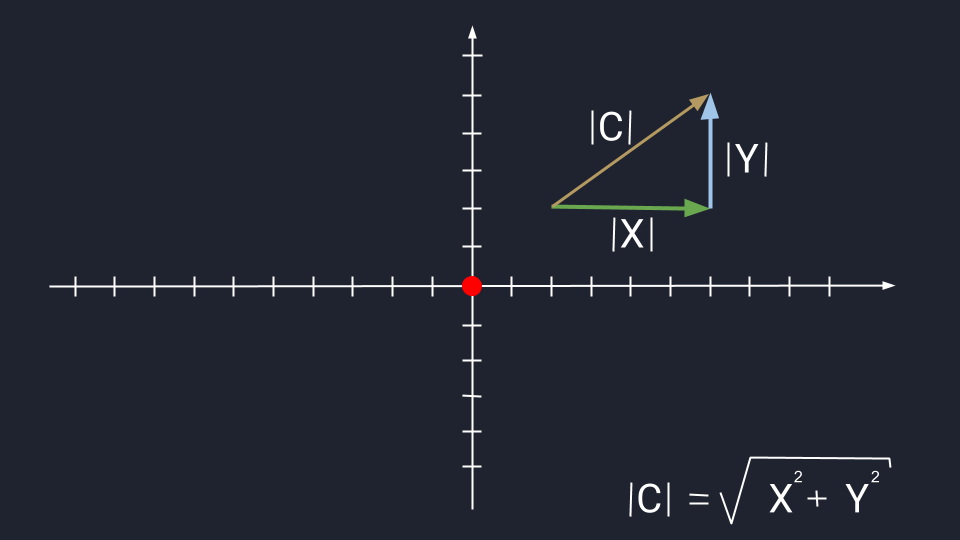
Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.
В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.
Видео:Сложение коллинеарных векторовСкачать

Умножение и деление вектора на число
Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.
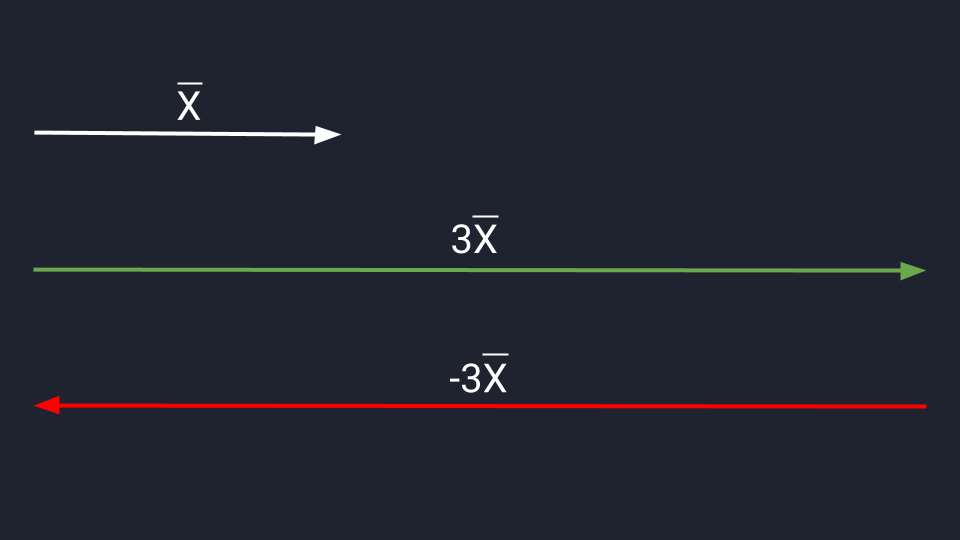
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.
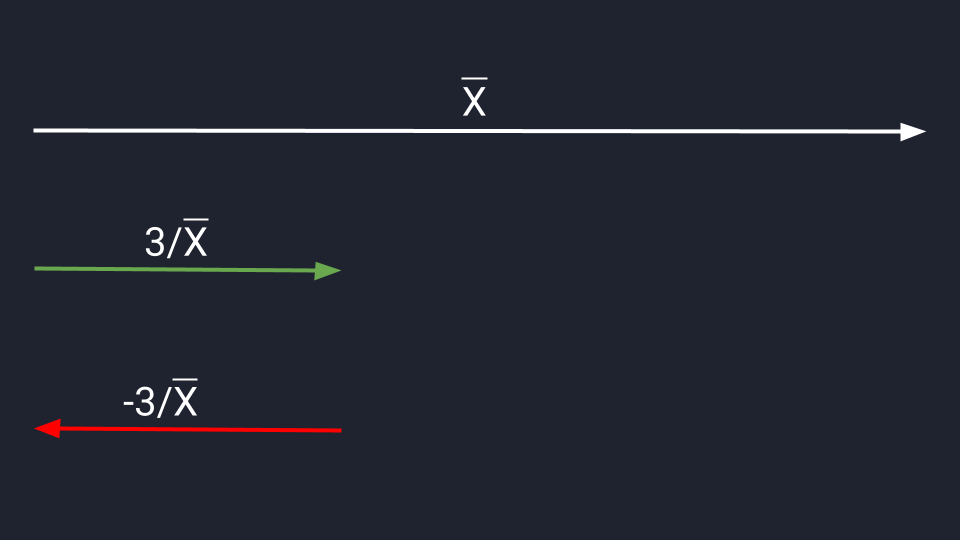
Видео:Вычитание векторов. 9 класс.Скачать

Да вроде несложно!
Пока ничего сложного. Но если углубляться, вы узнаете, что:
- векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
- если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
- а перемножение матриц — это и есть машинное обучение.
Видео:Коллинеарные векторы.Скачать

Что дальше
В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.
Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Вычитание векторов

Средняя оценка: 4.6
Всего получено оценок: 143.
Средняя оценка: 4.6
Всего получено оценок: 143.
Вычитание векторов часто вызывает проблемы у учеников. Это связано с тем, что вычитание в геометрии нужно выполнять очень осторожно, чтобы не получалось отрицательных чисел. А вектор может быть отрицательным, положительным, нулевым – это вызывает много ошибок, которых можно избежать просто один раз разобравшись в вопросе.
Видео:85. Вычитание векторовСкачать

Вектор
Вектор – одно из самых интересных явлений в математике. Это первая величина во всем школьном курсе, которая имеет две характеристики: направление и размер. Вектором называют направленный отрезок, то есть отрезок, у которого стрелкой указали направление движения.
Представьте, вы прошли километр от дома до парка. Если поставить точку в начальном положении и стрелку в конечном, то результат движениям будет являться вектором. Ведь он имеет направление: от дом до парка. При этом у результата движения есть и размер, в нашем случае это один километр.
Ученики часто пугаются отрицательных векторов, но в этом нет ничего страшного. Вектор это направление некого движения, а любое движение относительно, то есть зависит от системы отсчета.
В любую систему отчета входит точка отчета, система координат и прибор для измерения времени.
Если вектор поместить в любую систему координат, даже если это будет простой координатный луч, то вектор может быть направлен в одну сторону с системой координат, но может и в разные. Если вектор и система координат направлены в разные стороны, то вектор будет отрицательным.
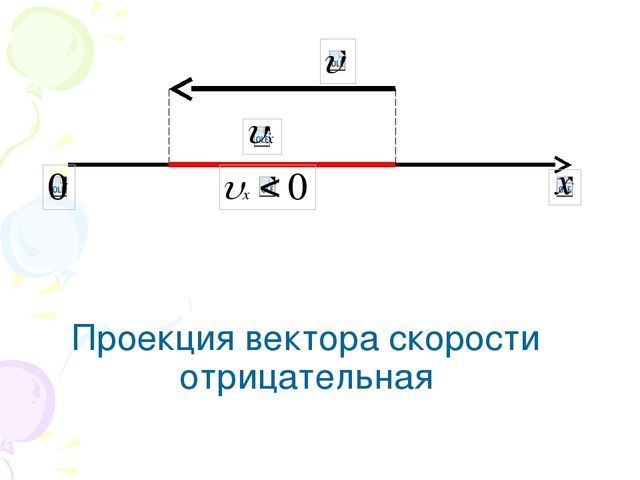
При этом противоположным направлением считается любое в половине плоскости, в другую сторону которой направлен вектор.
Видео:Понятие вектора. Коллинеарные векторы.Скачать
Особые случаи векторов
Первый вопрос, который возникает у множества учеников, это возможность существования нуля в системе векторов. Ноль у векторов есть, только это не число, а точка. Любую точку можно считать нулевым вектором. Нулевой вектор появляется в результате сложения коллинеарных разнонаправленных векторов.
Коллинеарными называют вектора, которые лежат на одной прямой. Эти векторы могут быть сонаправлены или противоположно направлены. При этом векторы, которые лежат на одной прямой так же считаются коллинеарными, так как любая прямая параллельна самой себе. Это не трудно понять, но запомнить название лучше наизусть, так как в тематике векторов, это определение встречается довольно часто.
Результат сложения или вычитания коллинеарных векторов будет коллинеарным для каждого из начальных построений. Поэтому найти результат такой операции можно арифметически, да и построить треугольник или параллелограмм из коллинеарных векторов не получится.
Видео:Координаты вектора. 9 класс.Скачать

Вычитание векторов
Результатом вычитания векторов может быть:
- Вектор. Если вычитание производилось в системе координат, то результат может быть положительным или отрицательным
- Нулевой вектор или точка
- Никаких других результатов быть не может
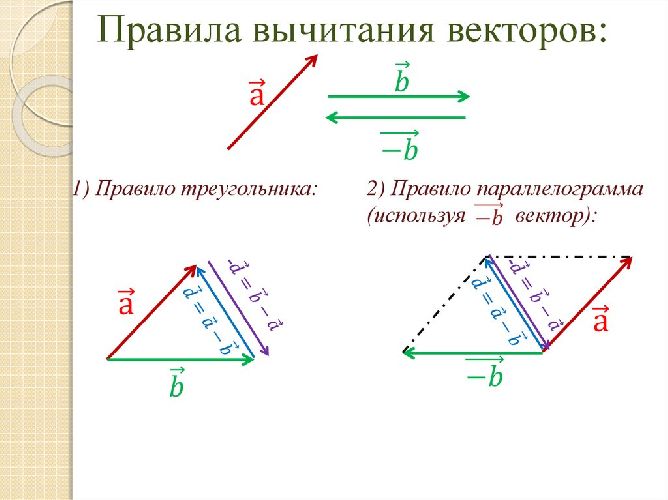
Для того, чтобы вычесть один вектор из другого, любой из векторов заменяется на противоположный и выполняется сложение по правилу треугольника или параллелограмма. Таким образом, меняется знак вектора.
В математической записи это выглядит так:
АВ-МР=АВ+РМ – в математической записи первая буква означает начало вектора, вторая – конец. Так можно без чертежа обозначить направление.
Видео:10 класс, 43 урок, Компланарные векторыСкачать

Что мы узнали?
Мы поговорили о векторах и их частных случаях. Обсудили, как правильно вычитать вектора и что может получиться в результате такого вычитания. Привели пример правильной записи вычитания 2 векторов.
Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Сумма и разность векторов
В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Сумма векторов
Сложение векторов выполняется по правилу треугольника.
Геометрическая интерпретация:
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .
Для сложения векторов также используется правило параллелограмма.
Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.
Формула сложения векторов
Элементы вектора c равняются попарной сумме соответствующих элементов a и b .
<table data-id="250" data-view-id="250_55602" data-title="Формулы сложения векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a + b = <ax + bx; ay + by> » data-order=» a + b = <ax + bx; ay + by> » style=»min-width:55.0847%; width:55.0847%;»> a + b = <ax + bx; ay + by>
<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a + b = <ax + bx; ay + by; az + bz> » data-order=» a + b = <ax + bx; ay + by; az + bz> «> a + b = <ax + bx; ay + by; az + bz>
<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a + b = <a1 + b1; a2 + b2; . an + bn> » data-order=» a + b = <a1 + b1; a2 + b2; . an + bn> «> a + b = <a1 + b1; a2 + b2; . an + bn>
Свойства сложения векторов
1. Коммутативность: a + b = b + a
2. Ассоциативность: ( a + b ) + c = a + ( b + c )
3. Прибавление к нулю: a + 0 = a
4. Сумма противоположных векторов: a + (- a ) = 0
Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.
Видео:Компланарны ли векторы: a=(2;5;8), b=(1;-3;-7) и c=(0;5;10)?Скачать

Разность векторов
Для вычитания векторов также применяется правило треугольника.
Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:
Формула вычитания векторов
Элементы вектора c равны попарной разности соответствующих элементов a и b .
<table data-id="251" data-view-id="251_83403" data-title="Формулы вычитания векторов" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>
<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" a — b = <ax — bx; ay — by> » data-order=» a — b = <ax — bx; ay — by> » style=»min-width:55.0847%; width:55.0847%;»> a — b = <ax — bx; ay — by>
<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" a — b = <ax — bx; ay — by; az — bz> » data-order=» a — b = <ax — bx; ay — by; az — bz> «> a — b = <ax — bx; ay — by; az — bz>
<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" a — b = <a1 — b1; a2 — b2; . an — bn> » data-order=» a — b = <a1 — b1; a2 — b2; . an — bn> «> a — b = <a1 — b1; a2 — b2; . an — bn>
Видео:Вектор. Определение. Коллинеарные векторы. Равные векторы.Скачать

Примеры задач
Задание 1
Вычислим сумму векторов и .
Задание 2
Найдем разность векторов и .
📺 Видео
Сложение векторов. 9 класс.Скачать

§15 Коллинеарность векторовСкачать
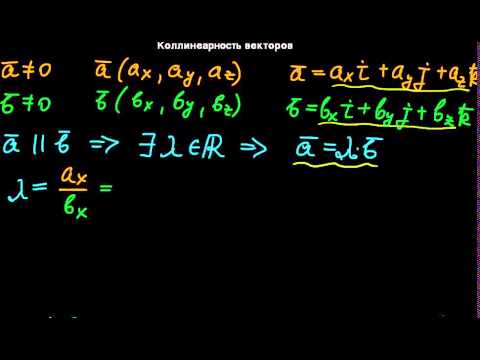
8 класс, 46 урок, Вычитание векторовСкачать