Как строить векторы скорости

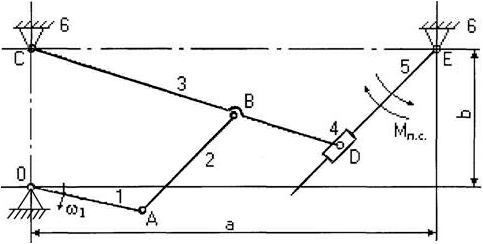
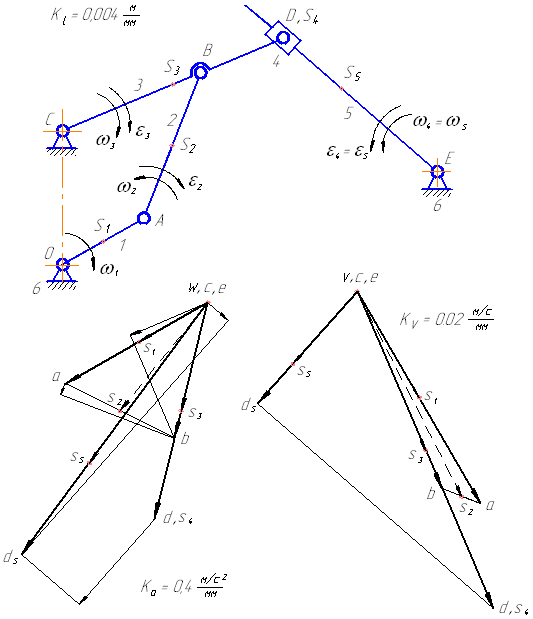
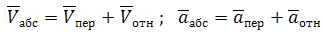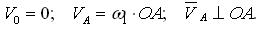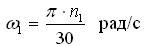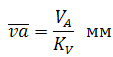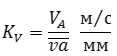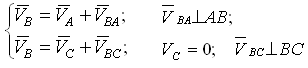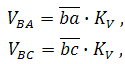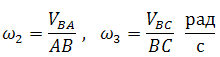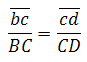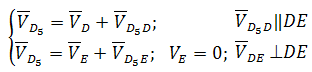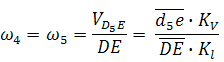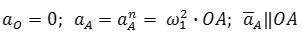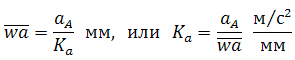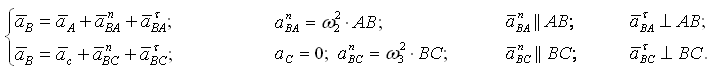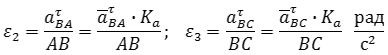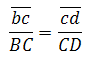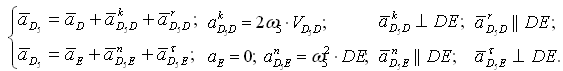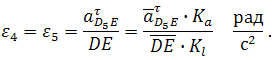Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:

На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.

На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.

Рисунок 1 – Кинематическая схема плоского рычажного механизма

Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.

По вычисленному значению V_A выбираем масштаб плана скоростей K_V и из произвольного полюса откладываем отрезок va изображающий эту скорость:

Можно также назначать отрезок va а масштаб K_V вычислять:

Истинные значения (в м/с) относительных скоростей V_BA и V_BC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:

а зная их, можно определить и угловые скорости звеньев 2 и 3:

Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:

Группа Ассура второго класса 3-го вида (звенья 4,5) :

где D₅ — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D₅ относительно точки E можно вычислить угловую скорость звеньев 4 и 5 ( ω₄=ω₅ , т. к. эти звенья соединяются поступательной парой):

Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.

План ускорений строится в таком же порядке.

Видео:Физика | Ликбез по векторамСкачать

Начальный механизм

Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена ( ω₁=соnst ):

По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):

Здесь точка w – полюс плана ускорений.

Группа Ассура (звенья 2,3) второго класса 1-го вида:

После построения определяются a τ _BA и a τ _BC , по которым можно вычислить угловые ускорения звеньев 2 и 3:

Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:

Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма

Группа Ассура (звенья 4,5) второго класса 3-го вида:

Для определения направления a k _D5D надо вектор V_D5D повернуть на 90° в направлении ω₅ . Угловые ускорения:

При силовом расчете необходимо иметь ускорения центров масс ( a_si ), которые на плане ускорений определяются методом подобия.

Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.

Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.

Таблица 1 – Кинематический анализ групп Ассура II класса методом планов

Видео:Физика: Понятие Вектор, Вектор СкоростиСкачать

Вектор скорости точки

Одной из основных кинематических характеристик движения точки является скорость. Скорость характеризуется не только численным значением, но и направлением, т. е. скорость является векторной величиной.

Рассмотрим перемещение точки Мза малый промежуток времени At (рис. 1.53):

Тогда V_cp = -^ — средняя скорость — вектор, равный отношению

вектора перемещения А г к промежутку времени, за который произошло это перемещение.

Скорость точки в данный момент времени — предельное значение вектора, следовательно, вектор скорости точки в данный момент времени равен скорости точки при стремлении At к 0, т.е.

Следовательно, вектор скорости точки в данный момент времени равен производной от радиус-вектора по времени.

Поскольку секущая в пределе переходит в касательную V , то скорость точки есть вектор, направленный по касательной к траектории в сторону движения точки.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Вектор ускорения точки

Ускорением точки называется векторная величина, которая характеризует изменение с течением времени модуля и направления скорости.

За промежуток времени At скорость точки

получила приращение AV = V_X-V (рис. 1.54).

Перенесем вектор V в точку Ми построим па-

раллелограмм для нахождения Д V.

Отношение приращения вектора скорости Д V к промежутку времени At определит вектор среднего ускорения точки М за этот промежуток времени:

Вектор среднего ускорения имеет то же направление, что ДК, т.е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени / называется векторная величина а , к которой стремится среднее ускорение а_ср при стремлении промежутка времени Дt к 0:

С учетом формулы (1.27):

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.

Видео:Сложение векторов. 9 класс.Скачать

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Видео:Построение проекции вектора на осьСкачать

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Видео:Построение плана скоростей. ТММСкачать

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Видео:Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Видео:#635 НАУКА Структура вакуума. Устройство Мироздания: версия Межзвездного Союза. Юмор в разных мирах.Скачать

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

🎥 Видео

С 21 января Плутон в Водолее 2024-2044 Новая эра. Кардинальное изменение жизни. Подробно каждый знакСкачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Вычитание векторов. 9 класс.Скачать

Построить разность векторов.Скачать

ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Урок 8. Векторные величины. Действия над векторами.Скачать

Мгновенная скорость (видео 6)| Векторы. Прямолинейное движение | ФизикаСкачать

Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

Как найти проекцию вектора скорости и ускорения. Выполнялка 112Скачать

Мгновенный центр скоростейСкачать