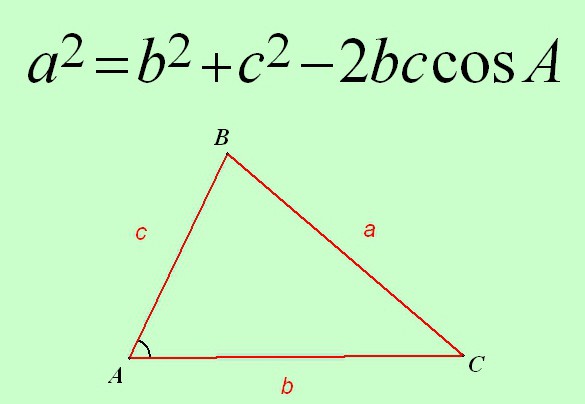Не все школьники, а тем более взрослые, знают, что теорема косинусов напрямую связана с теоремой Пифагора. Точнее сказать, последняя является частным случаем первой. Этот момент, а также два способа доказательства теоремы косинусов помогут стать более знающим человеком. К тому же практика в выражении величин из исходных выражений хорошо развивает логическое мышление. Длинная формула изучаемой теоремы обязательно заставит потрудиться и посовершенствоваться.
- Начало разговора: введение обозначений
- Формулировка и математическая запись
- Распространенное доказательство теоремы
- Доказательство теоремы через векторы
- Формулы для других сторон и всех углов
- Как без вычисления косинуса узнать вид угла?
- Первая задача
- Задача №2
- Третья задача
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Теорема косинусов через векторы
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Как формулируется и доказывается теорема косинусов?
- Начало разговора: введение обозначений
- Формулировка и математическая запись
- Распространенное доказательство теоремы
- Доказательство теоремы через векторы
- Формулы для других сторон и всех углов
- Как без вычисления косинуса узнать вид угла?
- Первая задача
- Задача №2
- Третья задача
- Сложение векторов: длина суммы векторов и теорема косинусов
- Определения скалярного произведения векторов через угол между ними
- Сложение векторов — решение примеров
- Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Начало разговора: введение обозначений
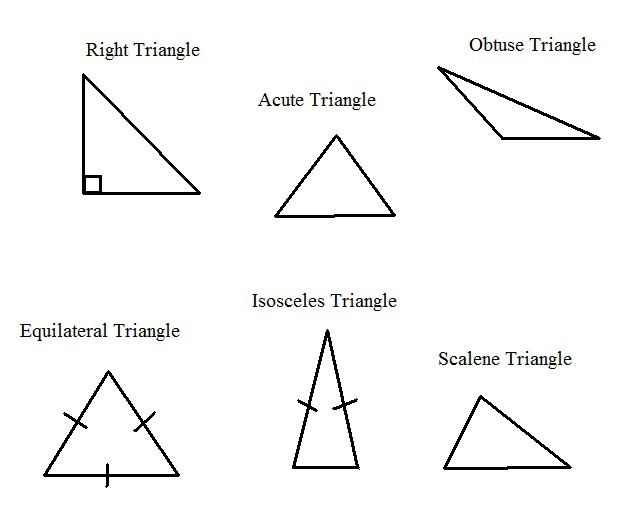
Эта теорема формулируется и доказывается для произвольного треугольника. Поэтому ею можно воспользоваться всегда, в любой ситуации, если даны две стороны, а в некоторых случаях три, и угол, причем необязательно между ними. Каким бы ни был вид треугольника, теорема сработает всегда.
А теперь про обозначение величин во всех выражениях. Лучше сразу договориться, чтобы потом несколько раз не пояснять. Для этого составлена следующая таблица.
| Элемент треугольника | Его обозначение |
| Неизвестная сторона | а |
| Две другие стороны | в, с |
| Угол, лежащий напротив неизвестной стороны | А |
| Углы, которые лежат против других сторон | В, С |
| Высота из вершины треугольника | н |
Видео:9 класс, 14 урок, Теорема косинусовСкачать

Формулировка и математическая запись
Итак, формулируется теорема косинусов следующим образом:
Квадрат стороны любого треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих же сторон на косинус угла, лежащего между ними.
Конечно, оно длинное, но если понять его суть, то запомнить будет просто. Можно даже представлять себе чертеж треугольника. Наглядно всегда проще запоминать.
Формула же этой теоремы будет выглядеть так:
а 2 = в 2 + с 2 — 2 * в * с * cos А.
Немного длинно, но все логично. Если немного внимательнее посмотреть, то можно увидеть, что буквы повторяются, значит, и запомнить ее несложно.
Видео:Теорема косинусов | ДоказательствоСкачать

Распространенное доказательство теоремы
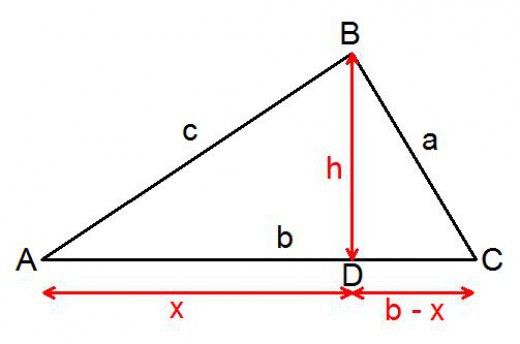
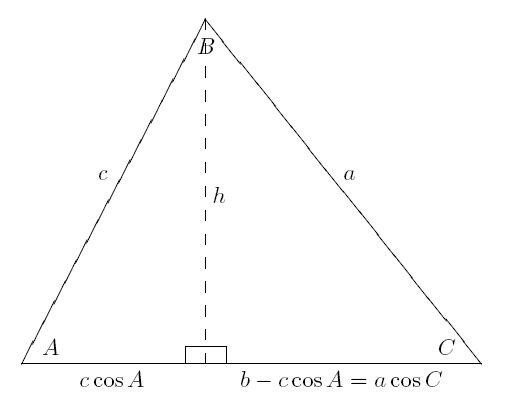
Поскольку она справедлива для всех треугольников, то можно выбрать для рассуждений любой из видов. Пусть это будет фигура со всеми острыми углами. Рассмотрим произвольный остроугольный треугольник, у которого угол С больше, чем угол В. Из вершины с этим большим углом нужно опустить перпендикуляр на противоположную сторону. Проведенная высота разделит треугольник на два прямоугольных. Это потребуется для доказательства.
Сторона окажется разделенной на два отрезка: х, у. Их нужно выразить через известные величины. Та часть, которая окажется в треугольнике с гипотенузой, равной в, выразится через запись:
Другая будет равна такой разности:
Теперь нужно записать теорему Пифагора для двух получившихся в результате построения прямоугольных треугольников, принимая за неизвестную величину высоту. Эти формулы будут выглядеть так:
н 2 = в 2 — (в * cos А) 2 ,
н 2 = а 2 — (с — в * cos А) 2 .
В этих равенствах стоят одинаковые выражения слева. Значит, их правые части тоже будут равны. Это просто записать. Теперь нужно раскрыть скобки:
в 2 — в 2 * (cos А) 2 = а 2 — с 2 + 2 с * в * cos А — в 2 * (cos А ) 2 .
Если здесь выполнить перенос и приведение подобных слагаемых, то получится начальная формула, которая записана после формулировки, то есть теорема косинусов. Доказательство закончено.
Видео:Теоремы синусов и косинусов | Ботай со мной #029 | Борис ТрушинСкачать

Доказательство теоремы через векторы
Оно гораздо короче предыдущего. И если знать свойства векторов, то теорема косинусов для треугольника будет доказана просто.
Если стороны а, в, с обозначить соответственно векторами ВС, АС и АВ, то справедливо равенство:
Теперь нужно выполнить некоторые действия. Первое из них — это возведение в квадрат обеих частей равенства:
ВС 2 = АС 2 + АВ 2 — 2 АС * АВ.
Потом равенство нужно переписать в скалярном виде, учитывая то, что произведение векторов равно косинусу угла между ними на их скалярные значения:
ВС 2 = АС 2 + АВ 2 — 2 АС * АВ * cos А.
Осталось только вернуться к старым обозначениям, и снова получится теорема косинусов:
а 2 = в 2 + с 2 — 2 * в * с * cos А.
Видео:Теорема косинусов. Урок геометрии 9 класс.Скачать

Формулы для других сторон и всех углов
Чтобы найти сторону, из теоремы косинусов нужно извлечь квадратный корень. Формула для квадратов одной из других сторон будет выглядеть так:
с 2 = а 2 + в 2 — 2 * а * в * cos C.
Чтобы записать выражение для квадрата стороны в, нужно в предыдущем равенстве заменить с на в, и наоборот, и под косинусом поставить угол В.
Из основной формулы теоремы можно выразить значение косинуса угла А:
cos А = (в 2 + с 2 — а 2 ) / (2 в * с).
Аналогично выводятся формулы для других углов. Это хорошая практика, поэтому можно попробовать написать их самостоятельно.
Естественно, что запоминать эти формулы нет необходимости. Достаточно понимания теоремы и умения вывести эти выражения из ее основной записи.
Исходная формула теоремы дает возможность найти сторону, если угол лежит не между двумя известными. К примеру, нужно найти в, когда даны величины: а, с, А. Или неизвестна с, зато есть значения а, в, А.
В этой ситуации нужно перенести все слагаемые формулы в левую сторону. Получится такое равенство:
с 2 — 2 * в * с * cos А + в 2 — а 2 = 0.
Перепишем его немного в другом виде:
с 2 — (2 * в * cos А) * с + (в 2 — а 2 ) = 0.
Можно легко увидеть квадратное уравнение. В нем неизвестная величина — с, а все остальные даны. Поэтому его достаточно решить с помощью дискриминанта. Так будет найдена неизвестная сторона.
Аналогично получается формула для второй стороны:
в 2 — (2 * с * cos А) * в + (с 2 — а 2 ) = 0.
Из других выражений такие формулы тоже легко получить самостоятельно.
Видео:Теорема косинусов #shortsСкачать

Как без вычисления косинуса узнать вид угла?
Если внимательно посмотреть на формулу косинуса угла, выведенную ранее, то можно заметить следующее:
- знаменатель дроби — всегда положительное число, потому что в нем стоит произведение сторон, которые не могут быть отрицательными;
- значение угла будет зависеть от знака числителя.
- острым в ситуации, когда числитель больше нуля;
- тупым, если это выражение отрицательное;
- прямым при его равенстве нулю.
Кстати, последняя ситуация обращает теорему косинусов в теорему Пифагора. Потому что для угла в 90º его косинус равен нулю, и последнее слагаемое исчезает.
Видео:Теорема косинусовСкачать

Первая задача
Тупой угол некоторого произвольного треугольника равен 120º. О сторонах, которыми он ограничен, известно, что одна из них больше другой на 8 см. Известна длина третьей стороны, это 28 см. Требуется найти периметр треугольника.
Сначала нужно обозначить одну из сторон буквой «х». В таком случае другая будет равна (х + 8). Поскольку есть выражения для всех трех сторон, можно воспользоваться формулой, которую дает теорема косинусов:
28 2 = (х + 8) 2 + х 2 — 2 * (х + 8) * х * cos 120º.
В таблицах для косинусов нужно найти значение, соответствующее 120 градусам. Это будет число 0,5 со знаком минус. Теперь полагается раскрыть скобки, соблюдая все правила, и привести подобные слагаемые:
784 = х 2 + 16х + 64 + х 2 — 2х * (-0,5) * (х + 8);
784 = 2х 2 + 16х + 64 + х 2 + 8х;
3х 2 + 24х — 720 = 0.
Это квадратное уравнение решается через нахождение дискриминанта, который будет равен:
Д = 24 2 — 4 * 3 * (- 720) = 9216.
Поскольку его значение больше нуля, то уравнение имеет два ответа-корня.
Последний корень не может быть ответом задачи, потому что сторона обязательно должна быть положительной.
Итак, две стороны известны. Легко найти третью: 12 + 8 = 20 (см). Теперь можно ответить на вопрос задачи. Периметр треугольника определяется как сумма всех сторон:
24 + 12 + 20 = 60 (см).
Ответ: периметр равен 60 сантиметрам.
Видео:Теорема КосинусовСкачать

Задача №2
В треугольнике известны: с, равное 2 см; а, которое составляет 10 см; угол С величиной 120º. Требуется найти сторону в.
Для начала нужно воспользоваться теоремой косинусов и вывести из нее формулу квадратного уравнения, в которой неизвестной будет величина в:
с 2 = а 2 + в 2 — 2 * а * в * cos C
в 2 — (2 * а * cos С) * в + (а 2 — с 2 ) = 0.
В нее нужно подставить все известные в условии величины:
в 2 — (2 * 10 * cos 120º) * в + (10 2 — 2 2 ) = 0.
Теперь нужно сосчитать то, что возможно, чтобы упростить выражение:
в 2 — (20 * (-1/2)) * в + (100 — 4) = 0
в 2 + 10 * в — 96 = 0.
Это стандартное квадратное уравнение, которое нужно решить через нахождение дискриминанта:
Д = (10) 2 — 4 * 1 * (-96) = 484.
По формулам нужно произвести вычисления для неизвестной стороны:
в1 = (- 10 + 22) / 2 = 6 (см);
в2 = (- 10 — 22) / 2 = — 16 — этот корень не удовлетворяет решению задачи, потому что сторона не может быть отрицательной.
Ответ: неизвестная сторона равна 6 см.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Третья задача
В некотором треугольнике даны стороны: а, в, с, которые соответственно равны 6 см, 10 см и 8 см. Требуется вычислить угол А.
Снова нужно воспользоваться теоремой косинусов. Используется та ее запись, в которой есть косинус угла А, поскольку именно его необходимо вычислить. Вот написана сразу формула для косинуса неизвестного угла:
cos А = (в 2 + с 2 — а 2 ) / (2 в * с).
Осталось подставить значения сторон и выполнить все вычисления:
cos А = (10 2 + 8 2 — 6 2 ) / (2 * 8 * 10).
После возведения всех слагаемых в квадрат и умножения чисел из знаменателя:
cos А = (100 + 64 — 36) / (160).
После сложения и деления получается:
cos А = 128 / 160 = 0,8.
Теперь нужно воспользоваться таблицей Брадиса, чтобы узнать, чему равен угол А. Ближайшее значение угла для этого косинуса составляет 36º54´.
Видео:Доказательство теоремы косинусов.Скачать
Please wait.
Видео:9 класс, 13 урок, Теорема синусовСкачать

We are checking your browser. mathvox.ru
Видео:Теорема косинусов с доказательствомСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Шаталов за одну минуту доказывает теорему, на которую традиционно выделяется 45 минут урока!Скачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d12a7201d0490b1 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Теорема косинусов.Скачать
Теорема косинусов через векторы
Видео:Геометрия 9 класс (Урок№16 - Теорема косинусов.)Скачать

Please wait.
Видео:Олегу Тинькову запрещён вход на Мехмат МГУСкачать

We are checking your browser. mathvox.ru
Видео:ТЕОРЕМА КОСИНУСОВ 9 класс доказательствоСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Теорема синусов с доказательствомСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Cloudflare Ray ID: 6cd47ba3b8a016a7 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Как формулируется и доказывается теорема косинусов?
Не все школьники, а тем более взрослые, знают, что теорема косинусов напрямую связана с теоремой Пифагора. Точнее сказать, последняя является частным случаем первой. Этот момент, а также два способа доказательства теоремы косинусов помогут стать более знающим человеком. К тому же практика в выражении величин из исходных выражений хорошо развивает логическое мышление. Длинная формула изучаемой теоремы обязательно заставит потрудиться и посовершенствоваться.
Видео:ТЕОРЕМА КОСИНУСОВСкачать

Начало разговора: введение обозначений
Эта теорема формулируется и доказывается для произвольного треугольника. Поэтому ею можно воспользоваться всегда, в любой ситуации, если даны две стороны, а в некоторых случаях три, и угол, причем необязательно между ними. Каким бы ни был вид треугольника, теорема сработает всегда.
А теперь про обозначение величин во всех выражениях. Лучше сразу договориться, чтобы потом несколько раз не пояснять. Для этого составлена следующая таблица.
| Элемент треугольника | Его обозначение |
| Неизвестная сторона | а |
| Две другие стороны | в, с |
| Угол, лежащий напротив неизвестной стороны | А |
| Углы, которые лежат против других сторон | В, С |
| Высота из вершины треугольника | н |
Формулировка и математическая запись
Итак, формулируется теорема косинусов следующим образом:
Квадрат стороны любого треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих же сторон на косинус угла, лежащего между ними.
Конечно, оно длинное, но если понять его суть, то запомнить будет просто. Можно даже представлять себе чертеж треугольника. Наглядно всегда проще запоминать.
Формула же этой теоремы будет выглядеть так:
а 2 = в 2 + с 2 — 2 * в * с * cos А.
Немного длинно, но все логично. Если немного внимательнее посмотреть, то можно увидеть, что буквы повторяются, значит, и запомнить ее несложно.
Распространенное доказательство теоремы
Поскольку она справедлива для всех треугольников, то можно выбрать для рассуждений любой из видов. Пусть это будет фигура со всеми острыми углами. Рассмотрим произвольный остроугольный треугольник, у которого угол С больше, чем угол В. Из вершины с этим большим углом нужно опустить перпендикуляр на противоположную сторону. Проведенная высота разделит треугольник на два прямоугольных. Это потребуется для доказательства.
Сторона окажется разделенной на два отрезка: х, у. Их нужно выразить через известные величины. Та часть, которая окажется в треугольнике с гипотенузой, равной в, выразится через запись:
Другая будет равна такой разности:
Теперь нужно записать теорему Пифагора для двух получившихся в результате построения прямоугольных треугольников, принимая за неизвестную величину высоту. Эти формулы будут выглядеть так:
н 2 = в 2 — (в * cos А) 2 ,
н 2 = а 2 — (с — в * cos А) 2 .
В этих равенствах стоят одинаковые выражения слева. Значит, их правые части тоже будут равны. Это просто записать. Теперь нужно раскрыть скобки:
в 2 — в 2 * (cos А) 2 = а 2 — с 2 + 2 с * в * cos А — в 2 * (cos А ) 2 .
Если здесь выполнить перенос и приведение подобных слагаемых, то получится начальная формула, которая записана после формулировки, то есть теорема косинусов. Доказательство закончено.
Доказательство теоремы через векторы
Оно гораздо короче предыдущего. И если знать свойства векторов, то теорема косинусов для треугольника будет доказана просто.
Если стороны а, в, с обозначить соответственно векторами ВС, АС и АВ, то справедливо равенство:
Теперь нужно выполнить некоторые действия. Первое из них — это возведение в квадрат обеих частей равенства:
ВС 2 = АС 2 + АВ 2 — 2 АС * АВ.
Потом равенство нужно переписать в скалярном виде, учитывая то, что произведение векторов равно косинусу угла между ними на их скалярные значения:
ВС 2 = АС 2 + АВ 2 — 2 АС * АВ * cos А.
Осталось только вернуться к старым обозначениям, и снова получится теорема косинусов:
а 2 = в 2 + с 2 — 2 * в * с * cos А.
Формулы для других сторон и всех углов
Чтобы найти сторону, из теоремы косинусов нужно извлечь квадратный корень. Формула для квадратов одной из других сторон будет выглядеть так:
с 2 = а 2 + в 2 — 2 * а * в * cos C.
Чтобы записать выражение для квадрата стороны в, нужно в предыдущем равенстве заменить с на в, и наоборот, и под косинусом поставить угол В.
Из основной формулы теоремы можно выразить значение косинуса угла А:
cos А = (в 2 + с 2 — а 2 ) / (2 в * с).
Аналогично выводятся формулы для других углов. Это хорошая практика, поэтому можно попробовать написать их самостоятельно.
Естественно, что запоминать эти формулы нет необходимости. Достаточно понимания теоремы и умения вывести эти выражения из ее основной записи.
Исходная формула теоремы дает возможность найти сторону, если угол лежит не между двумя известными. К примеру, нужно найти в, когда даны величины: а, с, А. Или неизвестна с, зато есть значения а, в, А.
В этой ситуации нужно перенести все слагаемые формулы в левую сторону. Получится такое равенство:
с 2 — 2 * в * с * cos А + в 2 — а 2 = 0.
Перепишем его немного в другом виде:
с 2 — (2 * в * cos А) * с + (в 2 — а 2 ) = 0.
Можно легко увидеть квадратное уравнение. В нем неизвестная величина — с, а все остальные даны. Поэтому его достаточно решить с помощью дискриминанта. Так будет найдена неизвестная сторона.
Аналогично получается формула для второй стороны:
в 2 — (2 * с * cos А) * в + (с 2 — а 2 ) = 0.
Из других выражений такие формулы тоже легко получить самостоятельно.
Как без вычисления косинуса узнать вид угла?
Если внимательно посмотреть на формулу косинуса угла, выведенную ранее, то можно заметить следующее:
- знаменатель дроби — всегда положительное число, потому что в нем стоит произведение сторон, которые не могут быть отрицательными;
- значение угла будет зависеть от знака числителя.
- острым в ситуации, когда числитель больше нуля;
- тупым, если это выражение отрицательное;
- прямым при его равенстве нулю.
Кстати, последняя ситуация обращает теорему косинусов в теорему Пифагора. Потому что для угла в 90º его косинус равен нулю, и последнее слагаемое исчезает.
Первая задача
Тупой угол некоторого произвольного треугольника равен 120º. О сторонах, которыми он ограничен, известно, что одна из них больше другой на 8 см. Известна длина третьей стороны, это 28 см. Требуется найти периметр треугольника.
Сначала нужно обозначить одну из сторон буквой «х». В таком случае другая будет равна (х + 8). Поскольку есть выражения для всех трех сторон, можно воспользоваться формулой, которую дает теорема косинусов:
28 2 = (х + 8) 2 + х 2 — 2 * (х + 8) * х * cos 120º.
В таблицах для косинусов нужно найти значение, соответствующее 120 градусам. Это будет число 0,5 со знаком минус. Теперь полагается раскрыть скобки, соблюдая все правила, и привести подобные слагаемые:
784 = х 2 + 16х + 64 + х 2 — 2х * (-0,5) * (х + 8);
784 = 2х 2 + 16х + 64 + х 2 + 8х;
3х 2 + 24х — 720 = 0.
Это квадратное уравнение решается через нахождение дискриминанта, который будет равен:
Д = 24 2 — 4 * 3 * (- 720) = 9216.
Поскольку его значение больше нуля, то уравнение имеет два ответа-корня.
Последний корень не может быть ответом задачи, потому что сторона обязательно должна быть положительной.
Итак, две стороны известны. Легко найти третью: 12 + 8 = 20 (см). Теперь можно ответить на вопрос задачи. Периметр треугольника определяется как сумма всех сторон:
24 + 12 + 20 = 60 (см).
Ответ: периметр равен 60 сантиметрам.
Задача №2
В треугольнике известны: с, равное 2 см; а, которое составляет 10 см; угол С величиной 120º. Требуется найти сторону в.
Для начала нужно воспользоваться теоремой косинусов и вывести из нее формулу квадратного уравнения, в которой неизвестной будет величина в:
с 2 = а 2 + в 2 — 2 * а * в * cos C
в 2 — (2 * а * cos С) * в + (а 2 — с 2 ) = 0.
В нее нужно подставить все известные в условии величины:
в 2 — (2 * 10 * cos 120º) * в + (10 2 — 2 2 ) = 0.
Теперь нужно сосчитать то, что возможно, чтобы упростить выражение:
в 2 — (20 * (-1/2)) * в + (100 — 4) = 0
в 2 + 10 * в — 96 = 0.
Это стандартное квадратное уравнение, которое нужно решить через нахождение дискриминанта:
Д = (10) 2 — 4 * 1 * (-96) = 484.
По формулам нужно произвести вычисления для неизвестной стороны:
в1 = (- 10 + 22) / 2 = 6 (см);
в2 = (- 10 — 22) / 2 = — 16 — этот корень не удовлетворяет решению задачи, потому что сторона не может быть отрицательной.
Ответ: неизвестная сторона равна 6 см.
Третья задача
В некотором треугольнике даны стороны: а, в, с, которые соответственно равны 6 см, 10 см и 8 см. Требуется вычислить угол А.
Снова нужно воспользоваться теоремой косинусов. Используется та ее запись, в которой есть косинус угла А, поскольку именно его необходимо вычислить. Вот написана сразу формула для косинуса неизвестного угла:
cos А = (в 2 + с 2 — а 2 ) / (2 в * с).
Осталось подставить значения сторон и выполнить все вычисления:
cos А = (10 2 + 8 2 — 6 2 ) / (2 * 8 * 10).
После возведения всех слагаемых в квадрат и умножения чисел из знаменателя:
cos А = (100 + 64 — 36) / (160).
После сложения и деления получается:
cos А = 128 / 160 = 0,8.
Теперь нужно воспользоваться таблицей Брадиса, чтобы узнать, чему равен угол А. Ближайшее значение угла для этого косинуса составляет 36º54´.
Сложение векторов: длина суммы векторов и теорема косинусов
Определения скалярного произведения векторов через угол между ними
Сложение векторов по правилу треугольника (суммой векторов 






Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».
Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.
При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть 




где 

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:

В случае вычитания векторов (







косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.
Перейдём к примерам.
Сложение векторов — решение примеров
Пример 1. Векторы 






Решение. Из элементарной тригонометрии известно, что 
Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 2. Векторы 






Пример 3. Даны длины векторов 


Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:
Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.
Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:
Пример 4. Даны длины векторов 


Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:
Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между 

Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:
Пример 5. Векторы 




Два смежных угла, как нетрудно догадаться из приведённого в начале урока определения, в сумме составляют 180 градусов. Следовательно, смежный с прямым углом (90 градусов) угол — тоже прямой (тоже 90 градусов). Косинус такого угла равен нулю, то же самое относится и к косинусу смежного угла. Поэтому, подставляя это значение в выражения под корнем в формуле длины суммы и разности векторов, получаем нули как последние выражения — произведения под знаком корня. То есть длины суммы и разности данных векторов равны, вычисляем их:
Пример 6. Какому условию должны удовлетворять векторы 

1) длина суммы векторов равна длине разности векторов, т. е. 
2) длина суммы векторов больше длины разности векторов, т. е. 
3) длина суммы векторов меньше длины разности векторов, т. е. 
Находим условие для первого соотношения. Для этого решаем следующее уравнение:
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.
Находим условие для второго соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).
Находим условие для третьего соотношения. Решаем уравнение:
Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.