С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
- Решение треугольника по трем сторонам
- Решение треугольника по двум сторонам и углу между ними
- Решение треугольника по стороне и любым двум углам
- Решение задач по математике онлайн
- Калькулятор онлайн. Решение треугольников.
- Решение треугольников
- Корзина
- Решение треугольников через синус и косинус угла
- 🔍 Видео
Видео:9 класс, 15 урок, Решение треугольниковСкачать

Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
 | (1) |
 | (2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
 . . |
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Видео:9 класс. Геометрия. Решение треугольниковСкачать

Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
 . . |
 . . |
Далее, из формулы
 . . |
 . . | (3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
 . . |
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
 , , |
   . . |
Из формулы (3) найдем cosA:
  |
 . . |
Поскольку уже нам известны два угла то находим третий:
  . . |
Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
 . . |
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Видео:9 класс, 13 урок, Теорема синусовСкачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:КАК РЕШИТЬ ТРЕУГОЛЬНИК?Скачать

Калькулятор онлайн.
Решение треугольников.
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Эта математическая программа находит сторону ( c ), углы ( alpha ) и ( beta ) по заданным пользователем сторонам ( a, b ) и углу между ними ( gamma )
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Введите стороны ( a, b ) и угол между ними ( gamma ) Решить треугольник
Видео:Геометрия 9 класс (Урок№17 - Решение треугольников. Измерительные работы.)Скачать

Решение треугольников
Корзина

Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,













Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».
Теоретический урок для решения задач по теме «Решение треугольников». Бесплатное обучение.
Содержание данной онлайн страницы электронного справочника по предмету математики для школьников:
- – задачи 76 — 77 представлены с примерами решений и ответами;
- – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 — 81;
- – решения, как найти угол, сторону треугольника, объясняются на данном уроке в контрольных работах 82 — 85.
Задача 76.


стороны треугольника a=10, b=7
Угол 

Решить треугольник: Угол по сторонам треугольника 




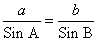
Sin B = 
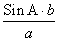

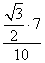

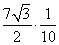

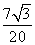
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы («Четырехзначные математические таблицы» Владимира Модестовича Брадиса)


Тогда 

Используя теорему синусов

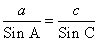

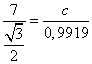



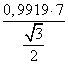
Ответ: 



Задача 77.
Треугольник ΔABC, стороны треугольника




Найти: Угол по сторонам треугольника 



Т.к. a=b=6,3, то треугольник ΔABC — равнобедренный.
Тогда 



Используя теорему синусов

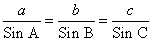

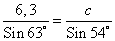



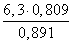

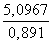
Ответ: 



Видео:9 класс, 14 урок, Теорема косинусовСкачать

Решение треугольников через синус и косинус угла
Задача 78.






Найти: угол треугольника 



Используя теорему синусов

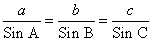

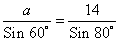



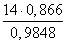

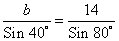



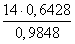
Ответ: 

Задача 79.


Найти: углы треугольника 






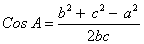
Cos B = 
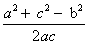

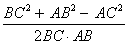

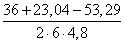

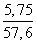
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла B


Используя формулу теоремы косинусов, находим косинус угла C
Cos C = 
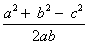

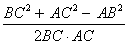
= 
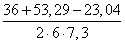
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла C


Тогда угол A равен 

Ответ: 





Задача 80.




Найти: угол 



Т.к. два угла в треугольнике равны 



Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов

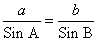
находим сторону BC=a





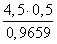
Ответ: 

Задача 81.
Треугольник ΔABC, длины трех его сторон
| 1) a=5 , b=c=4 Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным 1) Т.к. b=c=4, то треугольник ΔABC — равнобедренный, и, значит, остроугольный. Cos A = Тогда угол A равен 3) Используя формулу теоремы косинусов Cos B = Треугольник ΔABC, два угла и сторона Найти: длину всех сторон треугольника ΔABC = ? Зная размер двух углов в треугольнике ΔABC, находим третий угол Найдем угол Используя теорему синусов AC = (3 • 1) • 2 = 6 (м) Используя теорему синусов AB = Используя теорему синусов Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м. Три стороны a = 14, b = 18, все углы треугольника ΔABC = ? Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов Cos C = Cos C = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C Используя формулу теоремы косинусов Cos B = Cos B = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла B Следовательно, Ответ: Задача 84. Треугольник ΔEKP, сторона и два угла Найти: сторону треугольника PK = ? Используя теорему синусов Sin 115° = Sin (180° — 65°) = Sin 65° Тогда Задача 85. Треугольник ΔABC, две стороны и угол Найти: решить треугольник — определить значение стороны и двух углов (a, Используя формулу теоремы косинусов a = Используя формулу теоремы косинусов Cos C = Cos C = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C Следовательно, Ответ: a ≈ 13,8 ; 🔍 Видео9 класс, 12 урок, Теорема о площади треугольникаСкачать  №1025. С помощью теорем синусов и косинусов решите треугольник ABC, если:Скачать  Решение треугольниковСкачать  РЕШЕНИЕ ТРЕУГОЛЬНИКОВ. Контрольная № 1 Геометрия 9 класс.Скачать  Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать  КАК РЕШИТЬ ТРЕУГОЛЬНИК?Скачать  9 класс. Геометрия. Решение треугольников. Теорема косинусов. Теорема синусов. Урок #2Скачать  103. Решение треугольниковСкачать  Решение задачи с применением теоремы синусовСкачать  Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать  Решение треугольников | Геометрия 7-9 класс #98 | ИнфоурокСкачать  Соотношение между сторонами и углами треугольника. Решение треугольников. Урок 9. Геометрия 9 классСкачать  |


 2) Используя формулу теоремы косинусов
2) Используя формулу теоремы косинусов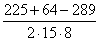 =
= 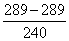 =0
=0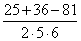 = —
= — 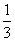
 Дано:
Дано: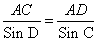 , находим сторону AC
, находим сторону AC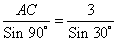
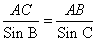 , находим сторону AB
, находим сторону AB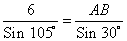
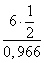 ≈ 3 (м)
≈ 3 (м)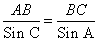 , находим сторону BC
, находим сторону BC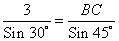
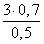 ≈ 4 (м)
≈ 4 (м)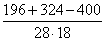 =
= 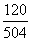 ≈ 0,24
≈ 0,24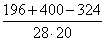 =
= 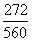 ≈ 0,4857
≈ 0,4857
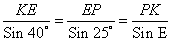 , находим сторону PK
, находим сторону PK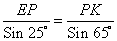
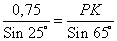
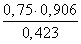 ≈ 1,61
≈ 1,61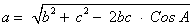 , получаем
, получаем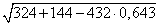 =
= 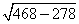 ≈ 13,8
≈ 13,8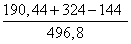 =
= 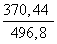 ≈ 0,7457
≈ 0,7457