В данной публикации мы рассмотрим, каким образом можно разложить вектор по двум базисным векторам, а также разберем пример решения задачи по этой теме.
Видео:Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать
Принцип разложения вектора
Для того, чтобы разложить вектор b по базисным векторам , требуется определить такие коэффициенты , при которых линейная комбинация векторов равняется вектору b , то есть:
Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать
Пример задачи
Разложим вектор по двум базисным векторам и .
Решение:
1. Векторное уравнение выглядит так:
3. Теперь нужно решить систему. Из второго уравнения получаем:
.
Подставляем полученное выражение в первое уравнение:
2 · (1 + 3y) + y = 16
2 + 6y + y = 16
7y = 14
y = 2
Следовательно, x = 1 + 3y = 1 + 2 · 2 = 7 .
Видео:Найдите разложение вектора по векторам (базису)Скачать
Разложение вектора по трём некомпланарным векторам. Задачи
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы напомним основные определения и рассмотрим типовые задачи на компланарные векторы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Видео:10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать
Лекция по математике на тему «Разложение вектора по трем некомпланарным векторам»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:Разложить вектор m по векторам a,b,cСкачать
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Лекция по теме «Разложение вектора по трем некомпланарным векторам»
Если вектор представлен в виде 
где x , y , и z — некоторые числа, то говорят, что вектор 
разложен по векторам 
, 
и 
. Числа x , y и z называются коэффициентами разложения.
Если
где x , y , и z — некоторые числа, то вектор 
разложен по векторам , и Числа x , y и z –
Докажем теорему о разложении вектора по трем некомпланарным векторам.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Теорема о разложении вектора по трем некомпланарным векторам.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Пусть , и — данные некомпланарные вектора. Докажем сначала, что любой вектор р можно представить в виде . Затем докажем единственность коэффициентов разложения.
Теорема о разложении вектора по трем некомпланарным векторам.
Дано: , и — некомпланарные; вектор
Доказать: 1) ;
2) коэффициенты разложения x , y и z определяются единственным образом.
Доказательство: Пусть , и — данные некомпланарные вектора 
Отметим произвольную точку О и отложим от нее векторы
. Через точку Р проведем прямую параллельную ОС. Р1 точка пересечения прямой с плоскостью АОВ (если Р принадлежит ОС, то в качестве Р1 возьмем точку О). Через Р1 проведем прямую Р1Р2 параллельную ОВ; Р2 точка пересечения этой прямой с ОА (если Р1 принадлежит ОВ то в качестве Р2 возьмем точку О);
2) По правилу многоугольника 
Заметим, что векторы ОР2 и ОА, Р2Р1 и ОВ. Р1Р и ОС коллинеарны. Значит, существуют такие числа x , y и z , что 
. Получаем, что
. Или ; Существование разложения доказано.
Теорема о разложении вектора по трем некомпланарным векторам.
Рисунок плоскости и векторов выходящих из одной точки.
1) ,
2) .
.
.
Или ;
Докажем единственность коэффициентов разложения. Допустим, что имеется ещё одно разложение вектора р
;
Вычитая это равенство из 
; получим
Теорема о разложении вектора по трем некомпланарным векторам.
что ;
Вычитая это равенство из
; получим
Это равенство выполняется только тогда, когда
, 
. Если предположить, например, что 
, то из этого равенства получим 
Тогда, векторы 
, 
и 
– компланарны. Это противоречит условию теоремы.
Значит, наше предположение неверно, 
, 
Следовательно, коэффициенты разложения определяются единственным образом. Теорема доказана.
, .
Если ,
то
Векторы , и – компланарны.
Противоречие условию теоремы, то есть ,
Коэффициенты разложения определяются единственным образом.
Разложите вектор BD 1 по векторам BA , ВС и ВВ 1 .
По правилу параллелепипеда вектор ВД1 равен сумме векторов ВА, ВС и ВВ1.
Разложите вектор BD 1 по векторам BA , ВС и ВВ 1 .
Решим эту же задачу под буквой б. Здесь нужно разложить вектор B 1 D 1 по векторам А 1 A , А 1 В и А 1 D 1 .
По правилу треугольника из треугольника А 1 В 1 D 1 :
Вектор В 1 D 1 равен сумме векторов B 1 A 1 + А 1 D 1 вектор В1 A 1 из А 1 В 1 B равен сумме .В 1 B + BA 1 . Вектор ВВ1 = АА1. Вектор ВА1 = – А1В.
Разложите вектор B 1 D 1 по векторам А 1 A , А 1 В и А 1 D 1
=
= 
.
📹 Видео
РАЗЛОЖЕНИЕ ВЕКТОРА по трем векторамСкачать
Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Как разложить вектор по базису - bezbotvyСкачать
Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать
Разложение вектора по базису. 9 класс.Скачать
Разложение вектора по векторамСкачать
Компланарность векторов. Объём пирамидыСкачать
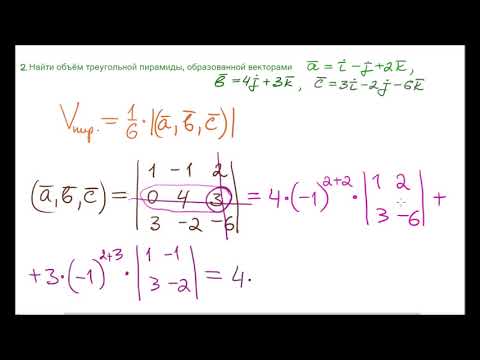
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
#вектор Разложение вектора по ортам. Направляющие косинусыСкачать
9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать
№363. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которогоСкачать
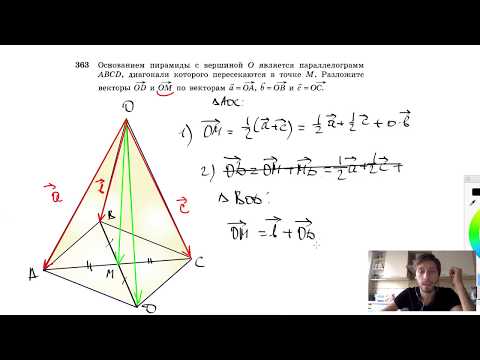
89. Разложение вектора по двум неколлинеарным векторамСкачать
§20 Нахождение объёма параллелипипедаСкачать
Разложение вектора по векторамСкачать
Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать
