 Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Окружность, вписанная в треугольник
- Определение окружности, вписанной в треугольник
- Теорема об окружности, вписанной в треугольник
- Презентация по геометрии 8 класс «Вписанная окружность Описанная окружность». презентация к уроку по геометрии (8 класс) на тему
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- По теме: методические разработки, презентации и конспекты
- 💡 Видео
Видео:Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||||||||
| Произвольный треугольник | ||||||
 | ||||||
| Равнобедренный треугольник | ||||||
 | ||||||
| Равносторонний треугольник | ||||||
 | ||||||
| Прямоугольный треугольник | ||||||
 | ||||||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность, вписанная в треугольник
Видео:№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Определение окружности, вписанной в треугольник
Определение 1. Окружностью, вписанной в треугольник называется окружность, которая находится внутри треугольника и касается всех его сторон (Рис.1).
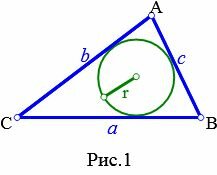 |
Можно дать и другое определение окружности, вписанной в треугольник.
Определение 2. Окружностью, вписанной в треугольник называется наибольшая окружность, которая может находится внутри треугольника.
При этом треугольник называется треугольником описанным около окружности . Центр вписанной в треугольник окружности явлется точка пересечения биссектрис треугольника. Центр окружности вписанной в треугольник называется инцентром треугольника.
Видео:Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Теорема об окружности, вписанной в треугольник
Теорема 1. В любой треугольник можно вписать окружность.
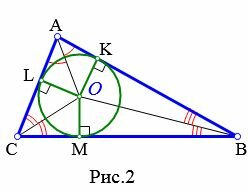 |
Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения биссектрис треугольника. Проведем из точки O перпендикуляры OK, OL и OM к сторонам AB, AC, BC, соответственно. Поскольку точка O равноудалена от сторон треугольника ABC, то OK=OL=OM. Тогда окружность с центром O и радиусом OK проходит через три точки K, L, M. Стороны AB, AC, BC треугольника ABC касаются этой окружности в точках K, L, M, поскольку они перпендикулярны к радиусам OK, OL, OM, соответственно. Следовательно, окружность с центром O и радиусом OK является вписанной в треугольник ABC.
Замечание 1. В любой треугольник можно вписать только одну окружность.
Доказательство. Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из этих окружностей равноудален от сторон треугольника и совпадает с точкой O пересечения биссектрис треугольника. Радиус этих окружностей равен расстоянию от точки O до сторон треугольника. Поэтому эти окружности совпадают.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Презентация по геометрии 8 класс «Вписанная окружность Описанная окружность».
презентация к уроку по геометрии (8 класс) на тему
Понятие окружности вписанной в треугольник и описанной около треугольника.
Видео:ГЕОМЕТРИЯ 8 класс : Вписанная окружностьСкачать

Скачать:
| Вложение | Размер |
|---|---|
| geometriya_8_klass_vpisannaya_okruzhnost_opisannaya_okruzhnost.ppt | 740 КБ |
Предварительный просмотр:
Видео:Вписанная окружность. Видеоурок по геометрии 8 классСкачать

Подписи к слайдам:
Геометрия 8 класс
Описанная окружность. Треугольник, вписанный в окружность. Окружность называется описанной около треугольника, если она проходит через все его вершины. В этом случае треугольник называется вписанным в окружность. Стороны вписанного треугольника являются хордами описанной около него окружности. Где лежит центр окружности, описанной около треугольника?
В Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника. А А
Треугольник. Описанная окружность . Центр описанной окружности – точка пересечения серединных перпендикуляров к сторонам треугольника. 2) Центр описанной окружности равноудалён от всех вершин треугольника. 3 ) Центр окружности, описанной около прямоугольного треугольника, является серединой гипотенузы.
Треугольник. Описанная окружность 4 ) R – радиус описанной окружности R=OA=OB=OC в любом треугольнике. 5) Центр окружности, описанной около тупоугольного треугольника, находится вне треугольника. — для правильного треугольника
Касательная к окружности Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности Общая точка окружности и касательной называется точкой касания. Что можно сказать о сторонах треугольника С D Е по отношению к окружности?
Окружность, вписанная в треугольник. Окружность называется вписанной в треугольник, если она касается всех его сторон. В этом случае треугольник называется описанным около окружности. Где лежит центр окружности, вписанной в треугольник? Треугольник ABC- описанный около окружности. Какие из треугольников AOM, MOB, BON, NOC, COK, KOA- равные ?
В С А М К Р Центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника. О
В любой треугольник можно вписать окружность.
Треугольник. Вписанная окружность. 1) Центр вписанной окружности в треугольник – точка пересечения биссектрис. 2) Центр вписанной окружности равноудалён от сторон треугольника. 3) p – полупериметр треугольника, r – радиус вписанной окружности p — полупериметр В правильном треугольнике C – гипотенуза
В правильном треугольнике R r
№ 1. В равносторонний треугольник со стороной 4 см вписана окружность. Найдите её радиус. а r S = S = = P = ½ ·4 · 3 = ½ · 12 = 6(см) — полупериметр r r = (см) Решение: S = p · r и (см) Ответ:
№ 2. Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см. А В С М К Р 4 3 6 Отрезки касательных, проведенных из одной точки равны. ВМ = ВК АМ = АР СР = СК 6 3 4 АВ = 10 АС = 7 ВС = 9 Р = 10 + 7 + 9 = 26
№ 3. Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см. А В С Центр описанной около п/у треугольника окружности лежит на середине гипотенузы . d = AC 15 АС = 35
№ 4. Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см . 0 А В 20 С 24 Т.к. ОК АС, то АК=КС=10 К по т. Пифагора ОС =
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

По теме: методические разработки, презентации и конспекты
презентация по геометрии 9 класс «Уравнение окружности»
презентация предназначена для введения темы и поможет повторить изученный материал по теме «Уравнение окружности».
презентация к уроку математики «Окружность. Длина окружности.» (6 класс )
В презентации дан устный счёт для определении темы урок, практическая работа и набор задач для нахождения длины окружности.
Презентация к уроку геометрии 8 класса по теме » Описанная окружность»
Презентация к уроку.
Презентация по геометрии 8 класс Вписанная окружность. Описанная окружность.
Данная презентация содержит определения и свойства вписанной окружности и описанной окружности около многоугольника (треугольник). В презентации рассмотрены несложные задачи.
Задачник по геометрии «Вписанные и описанные окружности»
ВПИСАННЫЕ И ОПИСАННЫЕ ОКРУЖНОСТИТреугольникК окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного.
Разноуровневая самостоятельная работа по геометрии «Вписанная и описанная окружность» (8 класс)
Разноуровневая самостоятельная работа по геометрии на тему «Вписанная и описанная окружность», 8 класс.Предназначена для закрепления пройденного материала. Содержит три уровня сложности, в к.
Презентация «Правильный многоугольник.Вписанная и описанная окружности»
Презентация к уроку «Правильный многоугольник.Вписанная и описанная окружности".
💡 Видео
8 класс, 38 урок, Вписанная окружностьСкачать

Геометрия 8 класс (Урок№33 - Описанная окружность.)Скачать

Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать

Окружность, вписанная в прямоугольный треугольник | Геометрия 8-9 классыСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

8 класс Геометрия. Окружность вписанная в четырехугольник и описанная около четырехугольника Урок #4Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Построить описанную окружность (Задача 1)Скачать

Урок по теме ВПИСАННАЯ ОКРУЖНОСТЬСкачать



































