Как разделить четырехугольник на 2 равные части

С одной стороны, разделить отрезок на равные части несложно, но с другой стороны, при этом могут появиться и трудности. Разбить какой-либо промежуток на равные части требуется не только для решения задач по геометрии, но и во многих областях жизни. В бытовой ситуации, например, такое деление может потребоваться для того, чтобы повесить картину на стене или установить мебельный гарнитур в определённой части комнаты.

Видео:Разрежь на две равные части и получи квадратСкачать

Два одинаковых значения

Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.

При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.

Видео:Делим четырехугольник на две равные частиСкачать

Получение четырех частей

В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.

Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.

Видео:Задача на логику как разрезать на две части и получить квадрат?Скачать

Разложение при помощи циркуля

Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:

• одну — из точки А;
• вторую — из точки Е.

И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.

Видео:Деление отрезка на 2,4,8 равных частей с помощью циркуля и линейкиСкачать

Теорема Фалеса

Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.

Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.

Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.

Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия:

• делить прямоугольник на несколько одинаковых прямоугольников;
• разделять треугольник, а соответственно, и его угол на две и более частей;
• рассекать прямой угол на три равных угла;
• разбивать окружность на одинаковые участки.

Все эти знания важны в машиностроении при вычерчивании деталей, а также активно применяются в инженерных работах.

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Четырехугольник

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Определение четырехугольника

Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.

Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.

Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.

Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Виды четырехугольников

Четырехугольники бывают следующих видов:

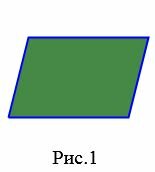
• Параллелограмм − четырехугольник, у которого противоположные стороны попарно вправны и параллельны (Рис.1).
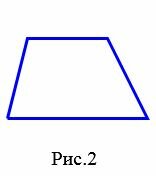
• Трапеция − четырехугольник, у которого две противоположные стороны параллельны (Рис.2).
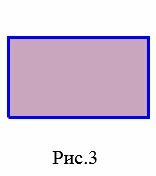
• Прямоугольник − четырехугольник, у которого все углы прямые (Рис.3).
• Ромб − четырехугольник, у которого все стороны равны (Рис.4).
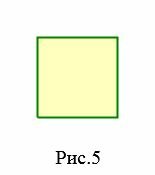
• Квадрат − четырехугольник, у которого все стороны равны и все углы прямые (Рис.5).
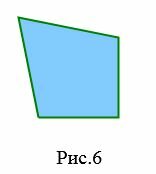
• Дельтоид − четырехугольник, у которого есть две пары равных смежных сторон (Рис.6, Рис.6.1).
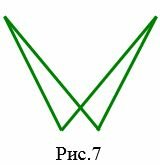
• Антипараллелограмм (или контрпараллелограмм)− четырехугольник, у которого противоположные стороны равны но не параллельны (с самопересечением) (Рис.7).

Видео:Как разделить 10 литров молока на две равные части? Задача на переливанияСкачать

Обозначение четырехугольника

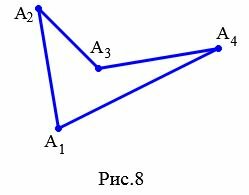
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют ( small A_1A_2A_3A_4 ) или ( small A_4A_3A_2A_1 ) (Рис.8).

Видео:9 Разрезание на две конгруэнтные частиСкачать

Соседние вершины четырехугольника

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 8 вершины ( small A_2 ) и ( small A_3 ) являются соседними, так как они являются концами стороны ( small A_2A_3. )

Видео:Как разделить круг на равные частиСкачать

Смежные стороны четырехугольника

Стороны четырехугольника называются смежными, если они имеют общую вершину.

На рисунке 8 стороны ( small A_2A_3 ) и ( small A_3A_4 ) являются смежными, так как они имеют общую вершину ( small A_3. )

Видео:Как разделить угол на равные части с помощью циркуляСкачать

Простой четырехугольник. Самопересекающийся четырехугольник

Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

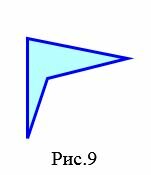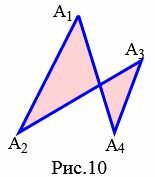На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны ( small A_1A_4 ) и ( small A_2A_3 ) пересекаются. Такой четырехугольник называется самопересекающийся.

Видео:Деление окружности на равные части с помощью циркуляСкачать

Выпуклый четырехугольник

Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

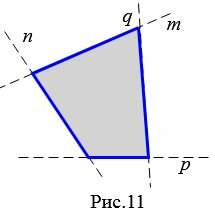На рисунке 11 четырехугольник лежит по одну сторону от прямых ( small m, n, p, q, ) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.

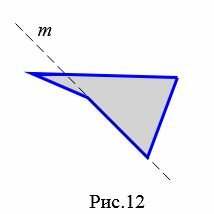На рисунке 12 прямая ( small m) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой ( small m). Следовательно, этот четырехугольник не является выпуклым.

Видео:Как разделить отрезок на две и четыре равные части циркулемСкачать

Правильный четырехугольник

Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.

На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Видео:Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Периметр четырехугольника

Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника ( small A_1A_2A_3A_4 ) периметр вычисляется из формулы:

Видео:🧭Как разделить круг на ТРИ Части, без Линейки и Циркуля; How to split a circle into three partsСкачать

Угол четырехугольника

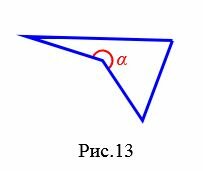
Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол ( small alpha ) на рисунке 13).

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Внешний угол четырехугольника

Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.

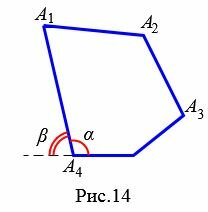На рисунке 14 угол α является внутренним углом четырехугольника при вершине ( small A_4, ) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.

Видео:Деление угла на равные части. Урок 5. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Диагональ четырехугольника

Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.

Очевидно, что у четырехугольника две диагонали.

Видео:Как выпуклый четырёхугольник разрезать по прямой, содержащей его вершину, на две равновеликие части?Скачать

Сумма углов четырехугольника

Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.

Видео:Разделить на 2,3 и 4 равные фигуры.Скачать

Сумма внешних углов четырехугольника

Пусть задан четырехугольник ( small A_1A_2A_3A_4 .) Внешний угол при вершине ( small A_1) равен ( small 180°-angle A_1.) Аналогично, внешние углы при вершинах ( small A_2, A_3, A_4 ) равны ( small 180°-angle A_2, ) ( small 180°-angle A_3, ) ( small 180°-angle A_4, ) соответственно. Тогда сумма внешних углов четырехугольника равна:

Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.

Решение. Рассмотрим произвольный четырехугольник ABCD (Рис.15). Покажем, например, что AB

Видео:1 2 3 деление окружности на 7 равных частейСкачать

Урок геометрии «Равновеликие фигуры в решении задач»

Разделы: Математика

Цель урока:

• повторение и обобщение ключевых задач о равновеликих фигурах;
• обучение учащихся поиску решения задач в ходе создания проблемно-познавательной ситуации;
• развитие грамотной устной и письменной математической речи учащихся.

Оборудование: доска, с заготовленными чертежами или слайды; раздаточный материал: учебное пособие Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса.

Ход урока

Заканчивая изучение темы «Площади», сегодня мы повторяем и развиваем наши знания о равновеликих фигурах.

1. Чтобы вспомнить понятие «равновеликие фигуры», поиграем в «Да» и «Нет».

Я составила диктант-попурри, выбрав вопросы из ваших диктантов, связанных с этим понятием. Я читаю вопрос, его автор комментирует правильный ответ.

Учащимся к семинару по теме «Площади» было предложено домашнее задание: составить диктант из пяти вопросов по данной теме, ответы на которые предполагали либо «да», либо «нет». Данную работу можно было выполнять группами по два человека, увеличив количество вопросов. Для быстрой проверки умения оперировать с понятиями при проведении диктантов используются сигнальные карточки: треугольники белого цвета и цветные треугольники, вырезанные из бумаги, при ответе «Да» учащиеся поднимают карточку белого цвета, при ответе «Нет» — цветной треугольник.

• Верно ли, что фигуры, имеющие равные площади, называются равновеликими?
• Верно ли, что равные многоугольники равновелики?
• Верно ли, что если площади фигур равны, то и фигуры равны?
• Могут ли равновеликие фигуры быть равными?
• Верно ли, что диагонали параллелограмма делят его на четыре равновеликих треугольника?

2. Какие ключевые (базовые) задачи о равновеликих треугольниках мы рассматривали?

№1. Медиана треугольника разделяет его на два равновеликих треугольника.

Обоснуйте это утверждение (открыть заготовленный рис. №1 и по ходу обоснования сделать запись, рисунок не стирать).

№2. Все треугольники с общим основанием, вершины которых лежат на прямой, параллельной основанию, равновелики.

Обоснуйте это утверждение (открыть рис. №2 и по ходу обоснования сделать запись, рисунок не стирать).

1) На рисунке 3 я начертила ломаную ADB. Сравните площади четырёхугольников ADBС и ADBХ, ответ обоснуйте.

Вывод:

Сколько четырёхугольников равновеликих четырёхугольнику ADBC можно построить на рисунке 3?

Ответ: бесконечно много.

Что для этого надо сделать?

Ответ: отметить точку на прямойm и соединить её с точками A и B.

Полученный четырёхугольник будет равновелик четырёхугольнику ADBC.

Какой результат я могла бы получить, если бы дополнила рисунок 3 ломаной из

3-х звеньев? 4-х звеньев?

Ответ: бесконечно много равновеликих пятиугольников, шестиугольников и т.д.

Показать рисунок 4.

2) Начертите выпуклый четырёхугольник ABCD. Проведите диагональ AC. (рис.5)

Как построить четырёхугольник, равновеликий четырёхугольнику ABCD, диагональ которого есть отрезок AC?

Ответ: провести прямую а такую, что а ll АС, и D.

Пусть E, четырёхугольник ABCD равновелик четырёхугольнику ABCE.
Докажите последнее утверждение.

3) Есть ли на Рис. 6 равновеликие треугольники?

Какое утверждение позволяет нам это доказать?

Пусть .

Можно ли выразить площадь четырёхугольника ABCO через и ?

Ответ: да,

Можно ли выразить площадь четырёхугольника ABCO через ?

Ответ: да,

Как связаны ?

Ответ:

4) Решим задачу о разбиении данного выпуклого четырёхугольника на две равновеликие части.

Прочитаем условие задачи № 130 [1]

№ 130. В выпуклом четырёхугольнике ABCD через середину O диагонали BD проведена прямая, параллельная диагонали AC. Она пересекает сторону AD в точке E.

Докажите, что .

Сделаем чертёж (рис.7).

На рисунке отметим, что точка О – середина BD и укажем, что EO ll AC. Итак, что мы должны доказать? . Обозначим . Какую часть должна составлять площадь каждой фигуры от S? Проанализируем условие, подумаем: по условию точка О – середина BD, какое утверждение, связанное с равносильностью фигур, мы могли бы использовать?

Ответ: медиана делит треугольник на два равновеликих треугольника.

Что нам надо провести на чертеже, чтобы можно было это утверждение применить?

Ответ: медианы АО и СО.

1. Проведём АО и СО.
2. 
3. по свойству медианы.
4. , по свойству 2 площадей.
   Какое условие мы не использовали?
   Ответ: EO ll AC.
   Можем ли мы сравнить площади четырёхугольников ABCE и ABCO?
5. т.к. EO ll AC, то , , .
6. , , значит, по свойству 2 площадей , ч.т.д.

Итог урока

Сегодня мы посвятили урок равновеликим многоугольникам. А где это может нам понадобиться, где практически можно применить полученные знания?

Пусть пройдёт какое-то время и кому-то из вас доведётся стать землеустроителем. Всем известно, что земледельцу не важно, какой формы участок, важна его площадь.

Допустим, что надо решить задачу: разделить участок на две части, равные по площади, если участок имеет форму: а) треугольника; б) четырёхугольника, при условии, что граница должна проходить через вершину многоугольника (столб на участке, например, стоит в этой вершине, и никому не хочется иметь его на своей земле).

Как выгоднее проводить границу: в виде ломаной или в виде отрезка прямой?

Ответ: длина отрезка меньше длины ломаной, соединяющей его концы, значит, если граница пройдёт по отрезку, то меньше материала уйдёт на ограждение.

Сформулируйте поставленную задачу на языке геометрии.

Ответ: а) Разделить треугольник на две равновеликие части прямой, проходящей через его вершину.

Как это сделать?

Ответ: Провести медиану из этой вершины.

Ответ: б) Разделить четырёхугольник на две равновеликие части прямой, проходящей через его вершину.

Как это сделать?

Решить задачу №130.

1. Провести АС.
2. Провести ВD.
3. Отметить точку О середину ВD.
4. Провести прямую mтакую, чтоm ll AC,
5. m пересекает CD в точке М
6. АМ – искомая граница.

Как разделить на две равновеликие части участок, имеющий форму пятиугольника?

Литература

1. Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса. М.: Просвещение, 1996.