Приведённые ниже текст является частью книги «Первый шаг в квантовую реальность».
6. Тригонометрическая форма комплексных чисел.
Пусть дано некоторое комплексное число с модулем
Очевидно, что причём
Поэтому существует некоторый угол , такой что
В результате получаем тригонометрическую форму комплексных чисел:
Угол называется аргументом комплексного числа.
Нам уже известно, что комплексные числа являются матрицами следующего вида:
Подставив сюда получим:
7. Геометрический смысл линейного преобразования, соответствующего комплексному числу в матричной форме.
Выясним геометрический смысл аргумента комплексного числа.
Только что нами получена матрица, изображающая любое комплексное число. Запишем соответствующее ей линейное преобразование, рассматривая при этом частный случай :
Пусть даны две точки и . Линейное преобразование переводит эти точки в и соответственно.
Скобки в подкоренном выражении равны:
Теперь вычислим сумму квадратов:
Удвоенные произведения здесь взаимно уничтожаются, поэтому
Это значит, что исследуемое линейное преобразование таково, что все расстояния сохраняются.
Для равенства треугольников необходимо и достаточно, чтобы были равны их стороны. Поэтому линейное преобразование преобразует любой треугольник в некоторый треугольник, равный исходному. Следовательно, в результате линейного преобразования сохраняются не только расстояния, но и углы.
Кроме того, непосредственно убеждаемся, что начало координат остаётся неизменным, иначе говоря, точка (0,0) переходит в точку (0,0).
Преобразование плоскости называется поворотом плоскости вокруг центра, если оно сохраняет расстояния и углы и, кроме того, оставляет низменной некоторую точку, называемую центром поворота.
Теперь возьмём произвольный треугольник с вершиной в начале координат. Рассматриваемое нами линейное преобразование преобразует его в точно такой же треугольник и тоже с вершиной в начале координат. Это значит, что, во-первых, произошёл поворот на некоторый угол относительно начала координат, и, во-вторых, все радиусы, исходящие из начала координат поворачиваются на один и тот же угол.
Теперь выясним, какой это угол.
С помощью формул поворота плоскости непосредственно убеждаемся, что точка (1, 0) переводится в точку :
Следовательно, поворот выполняется на угол .
Итак, поворот плоскости относительно начала координат на угол описывается формулами:
Это значит, что комплексное число
при изображает поворот плоскости против часовой стрелки на угол . Такое направление принято считать положительным.
Если , то повторяя приведённые выше соображения, получим, что , т.е. все расстояния пропорционально увеличиваются (при ) или уменьшаются (при ).
Короче, геометрический смысл комплексного числа таков: выполняется поворот всей плоскости на угол , при , и дополнительно выполняется преобразование подобия при .
А теперь вернёмся к матрице поворота на плоскости:
с учётом того, что , принимает вид:
У матриц поворота есть важное и полезное свойство: обратная матрица равна транспонированной:
Матрицы с действительными матричными элементами, у которых транспонированная и обратная матрица совпадают, называются ортогональными.
Определитель матрицы поворота равен 1, так как
Можно доказать, что определитель любой ортогональной матрицы равен ±1.
Видео:10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Комплексные числа и операции с ними
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Например функция определена для , аналогично можно вспомнить, что функция определена для 0″/>, а функция определена для .
Однако, ограниченная область определения функций на множестве вещественных чисел не означает, что , или не имеют смысла. Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том, что не может быть представлено вещественным числом. Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .
При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.
Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1), на которой мы можем откладывать рациональные и иррациональные вещественные числа. Но на этой прямой нет числа , значит его надо искать вне числовой прямой. Таким образом мы должны расширить множество вещественных чисел до множества в котором значения , или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве, как на множестве вещественных чисел.
Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано число .
Значение вещественного числа однозначно определяет его позицию на числовой прямой, однако для определения позиции на плоскости одного числа недостаточно.
Для «навигации» по комплексной плоскости вводятся две прямые и , которые пересекаются в начале координат. Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа. Прямая называется мнимой осью и она перпендикулярна реальной оси . Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.
Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно. При этом само комплексное число можно записать как , где называется реальной частью и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью и задает координату точки комплексной плоскости на мнимой оси .
Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей .
Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой .
Если и , тогда число является действительным и располагается на реальной оси .
Если и , тогда число является чисто мнимым и располагается на мнимой оси .
Если и , тогда число располагается в одной из четвертей комплексной плоскости.
Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как
Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Роль поворотного множителя при графическом изображении комплексных чисел
Выражение е 
вектор, изображающий комплексное число |А| е 
Показатель степени «j α» в выражении е 
При расчетах электрических цепей встречаются случаи вычислений с поворотным множителем, результаты которых полезно запомнить:
1. е 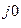
2. е 
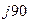
3. е 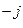
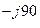
4. е 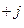
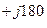

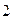
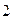
Таким образом, в результате умножения комплексного числа на поворотный множитель е 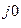
ется, во втором случае направление вектора совпадает с направление полуоси «+j»
( т.е. вектор расположен вверх ), в третьем случае вектор расположен вниз, в четвертом случае вектор в результате умножения поворачивается на 180º против часовой стрелке ( при + 180º ) или по часовой ( при — 180º ).
В последнем случае направление поворота не имеет значения, т.к. при повороте как против часовой, так и по часовой стрелке, вектор занимает положение, противо
В конце объяснения представим одно и тоже число А в разных формах:
1. в алгебраической А = 3 + j4;
2. в графической – в виде вектора на рис.2;
3. в тригонометрической А = 5 ( cos 53º + j sin53º );
4. в показательной А = 5 е 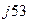
Таким образом, из четырех форм записи комплексного числа А только две –
алгебраическая и тригонометрическая, строго соответствуют понятию «комплекс-
ное число», т.е. такое число, которое состоит из нескольких частей.
Следует отметить, что при расчетах электрических цепей символическим методом часто приходится переходить от одной формы представления комплекс-
ного числа к другой, например, от алгебраической к показательной. Для таких переходов применяют простейшие действия над числами, а именно: сложение, вычитание, умножение и деление.
Часть 2. Действия с комплексными числами
Сложение и вычитание комплексных чисел
Для сложения и вычитания комплексных величин и чисел используют их алгебра-
ическую и графическую формы представления.
Сложение и вычитание комплексных чисел в алгебраической форме
При сложении комплексных чисел ( комплексов ) складываются отдельно их вещественные и мнимые составляющие, например,
А + В = ( А’ + j А» ) + ( В + j В» ) = ( А’ + В’ ) + j( А» + В» ) =
При вычитании комплексных чисел ( комплексов ) вычитаются отдельно их вещественные и мнимые составляющие, например,
А — В = ( А’ + j А» ) — ( В + j В» ) = ( А’ — В’ ) + j( А» — В» ) =
Вычитание комплексных чисел можно заменить простейшим действием элементарной алгебры, а именно — сложением уменьшаемого числа с вычитаемым, взятым с обратным знаком:
С = А – В + А + ( — В ),
С = ( А’ + j А» ) + ( — В – j В» ) = ( А’ — В’ ) + j( А» — В» ) =
Пример 5.Найти сумму С чисел А =3+j 4 и В = 5 + j 8.
Решение. Сумма С = А + В = 3+j 4 + 5 + j 8 = 8 + j 12.
Пример 6.Найти сумму С чисел А =4+j 6 и В = — 5 + j 8.
Решение. Сумма С = А + В = 4+j 6 + ( — 5 + j 8 ) = -1+ j14.
Пример 7. Найти разность С чисел А = 80 + j 90 и В = 50 – j 30.
Решение. Разность С = 80 + j 90 – ( 50 – j 30 ) = 80 + j90 – 50 + j 30 =
Пример 8. Найти сумму С чисел А = 10е 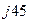
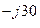
Решение. Выразим комплексные числа в алгебраической форме:
А = 10е 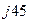
В = 6е 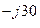
Сумма С = А + В = 7,07 + j7,07 + (5,2 – j3 ) = 12,27 + j4,07.
Преобразуем число С из алгебраической в показательную форму:
модуль суммы | C | = 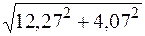
тангенс аргумента tg α = C»/ С’ = 4,07 / 12,27 = 0,331;
α = arc tg α = arc 0,331 = 18º20′;
число С = 12,9е 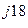
📹 Видео
2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

Аргумент комплексного числа. Часть 1Скачать

Угол между векторами. 9 класс.Скачать

Тригонометрическая форма комплексного числаСкачать

Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Аргумент комплексного числаСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

#225. КВАТЕРНИОНЫ и углы ЭйлераСкачать
Математика это не ИсламСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Матрица поворотаСкачать

Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Изобразить область на комплексной плоскостиСкачать

Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать

Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать


