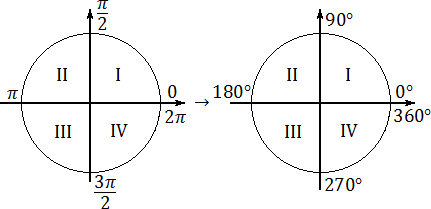
Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
- В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относ?
- Прошу, помогите?
- Углом какой четверти является угол альфа если альфа = — 10, альфа = 800, альфа = 10000?
- При каком значении параметра k точка пересечения прямых 2x + y = 9 и kx + 5y = 18 принадлежит биссектрисе четвертого координатного угла?
- Tg альфа = 3?
- Найдите sin(альфа + бета), если sin альфа = 0, 6 , sin бета = 0, 8 , альфа и бета углы 1й четверти?
- В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относ?
- Углом какой четверти является угол альфа если синус а меньше 0 и катангенс больше 0?
- В каком координатном угле координатной плоскости расположена данная точкаАменьше0, Бменьше0 = в какой четверти?
- В какой координатной четверти находятся углы равные — 150 , — 10, 800, 10000 гр?
- Косинус квадрат альфа минус косинус в четвертой степени альфа плюс синус в четвертой степени альфа = ?
- Радианная мера угла
- Переход от радианной меры к градусной
- Границы координатных четвертей
- Нестандартные углы и периодичность
- 📹 Видео
Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:10 класс, 11 урок, Числовая окружностьСкачать  В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относ?Алгебра | 5 — 9 классы В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относятся следующие углы альфа = — 920 альфа = — 1240 помогите пожалуйста чтоб правильно было. 1)Я так понял, надо определить, к какой четверти относится угол. — 20 — угол 4 четверти. — 135 — угол 3 четверти — 210 — угол 2 четверти — 350 — угол 1 четверти Во всех случаях мы идём по окружности по часовой стрелки и приходим в соответствующую четверть 2) — 30 — угол 4 четверти — 150 — угол 3 четверти — 360 — это граница между 1 и 4 четвертями Здесь рассуждали аналогично 3)выделим из угла — 920 полное число оборотов. — 920 = — 360 * 2 + 180 — 20 — то есть мы идём по окружности один оборот по часовой стрелки, затем в этом же направлении ещё полокружности и ещё в этом же напралвении угол в 20 градусов. Оказываемся во 2 четверти. — 920 — угол 2 четверти Здесь поступим также. Сначала выделим полное число оборотов и полуоборотов, если это возможно. — 1240 = — 360 * 3 — 160 = — 360 * 3 — 90 — 70 — мы идём по окружности по часовой стрелке и делаем сначала 3 полных оборота в этом направлении, затем в этом же направлении проходим ещё ровно одну четверть и ещё 70 градусов. Оказываемся в 3 четверти. Итак, угол в — 1240 градусов — угол 3 четверти. Видео:Тригонометрическая окружность. Как выучить?Скачать  Прошу, помогите?Определите, углом какой четверти является угло альфа, если : а) альфа = 179 градусов б) альфа = 325 градусов в) альфа = — 105 градусов г) альфа = — 10 градусов д) альфа = 800 градусов е) альфа = 10 000 градусов. Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать  Углом какой четверти является угол альфа если альфа = — 10, альфа = 800, альфа = 10000?Углом какой четверти является угол альфа если альфа = — 10, альфа = 800, альфа = 10000. Объясните как вы это решили пожалуйста. Видео:Найти знак тригонометрической функции (bezbotvy)Скачать 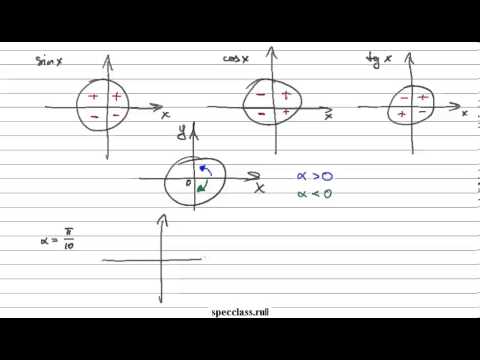 При каком значении параметра k точка пересечения прямых 2x + y = 9 и kx + 5y = 18 принадлежит биссектрисе четвертого координатного угла?При каком значении параметра k точка пересечения прямых 2x + y = 9 и kx + 5y = 18 принадлежит биссектрисе четвертого координатного угла? Видео:Формулы приведения - как их легко выучить!Скачать  Tg альфа = 3?Альфа принадлежит 3 четверти. Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Найдите sin(альфа + бета), если sin альфа = 0, 6 , sin бета = 0, 8 , альфа и бета углы 1й четверти?Найдите sin(альфа + бета), если sin альфа = 0, 6 , sin бета = 0, 8 , альфа и бета углы 1й четверти. Видео:1. Числовая окружность. 10 классСкачать  В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относ?В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относятся следующие углы альфа = — 920 альфа = — 1240 помогите пожалуйста чтоб правильно было. Видео:Период тригонометрических функций тангенс и котангенс в градусах В какой четверти находится угол поСкачать  Углом какой четверти является угол альфа если синус а меньше 0 и катангенс больше 0?Углом какой четверти является угол альфа если синус а меньше 0 и катангенс больше 0. Видео:5. Как найти точки на тригонометрической окружности. Отрицательные углы в градусах и радианах.Скачать  В каком координатном угле координатной плоскости расположена данная точкаАменьше0, Бменьше0 = в какой четверти?В каком координатном угле координатной плоскости расположена данная точка Аменьше0, Бменьше0 = в какой четверти? Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать  В какой координатной четверти находятся углы равные — 150 , — 10, 800, 10000 гр?В какой координатной четверти находятся углы равные — 150 , — 10, 800, 10000 гр. Видео:стр 15 #1.14 Алгебра 10 класс. Определите, углом какой четверти является уголСкачать  Косинус квадрат альфа минус косинус в четвертой степени альфа плюс синус в четвертой степени альфа = ?Косинус квадрат альфа минус косинус в четвертой степени альфа плюс синус в четвертой степени альфа = ? Вы зашли на страницу вопроса В каких координатных четвертях лежат конечные стороны след углов — 20 — 135 — 210 — 350 В каких координатных четвертях лежат конечные стороны след углов — 30 — 150 — 360 а также к какой четверти относ?, который относится к категории Алгебра. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке. Видео:Вычислить значение тригонометрического выражения sin(-300°)cos(-135°)tg(-210°)ctg(-120°)Скачать  Радианная мера углаВ школьном курсе математики есть два определения основных тригонометрических функций — синуса, косинуса, тангенса и котангенса:
Для решения задачи B11 нужен именно алгебраический подход. Чуть позже мы убедимся, что такие задачи решаются элементарно — буквально с помощью одной формулы. Но для начала научимся быстро (буквально на лету) определять координатную четверть, в которой расположен искомый угол. В этом нам помогут следующие правила. Видео:Период тригонометрических функций в радианах с числом Пи. В какой четверти находится угол поворота.Скачать  Переход от радианной меры к градуснойВспомните: в 8—9 классах мы работали лишь с несколькими стандартными углами. А именно: 30°, 45° и 60°. В особо продвинутых случаях учителя рассказывали еще об углах 90° и 0°. Любые другие значения назывались «сложными», и возникновение таких углов, скорее всего, указывало на ошибку в решении. С введением тригонометрической окружности все ограничения на углы отпадают. Здесь я не буду рассказывать, как устроена тригонометрическая окружность — все это подробно описано в любом учебнике по математике. Вместо этого предлагаю обсудить другой вопрос — более важный, но которому почему-то не уделяется достаточно внимания. Речь идет о переходе от радианной меры угла к градусной. Исторически так сложилось (и небезосновательно), что углы на тригонометрической окружности измеряют в радианах. Например, полный оборот — 360° — обозначается А всеми любимый (или ненавидимый) угол 45° равен У многих возникает вопрос: при чем здесь Так вот, чтобы избежать путаницы, запомните простое, но очень важное правило:
Обратите внимание: данное правило работает только для тригонометрических функций! Например, мы спокойно можем записать Но если мы хотим найти примерную длину придется считать: Разумеется, существует и обратное правило — переход от градусной меры угла к радианной. Однако нас это сейчас не интересует, поскольку в задачах B11 такой переход не встречается. Теперь взгляните на конкретные примеры:
Итак, перед нами восемь тригонометрических функций, аргументы которых заданы в радианах. Мы можем перейти от радианной меры аргументов к градусной по правилу: . Имеем:
Итак, вместо непонятного мы получаем вполне вменяемое число, которое можно умножать и делить по стандартным правилам. Видео:ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать  Границы координатных четвертейТеперь, когда мы умеем заменять радианную меру углов градусной, попробуем переписать всю тригонометрическую окружность. Это будет ключом к решению задачи B11. Основные правила останутся прежними: «нулевой градус» совпадает с положительным направлением , а углы откладываются в направлении против часовой стрелки. Но числа, стоящие на границах координатных четвертей, станут другими. Взгляните: Отныне вместо непонятных «пи» и «пи-пополам» используйте простую и понятную шкалу:
Хорошая новость состоит в том, что эти правила очень быстро откладываются в голове — стоит лишь немного потренироваться. И вы точно не забудете эти числа на ЕГЭ по математике, чего нельзя сказать про радианную меру. Если же память на числа плохая, могу посоветовать одну хитрость. Взгляните еще раз на границы координатных четвертей: 90°, 180°, 270° и 360°. Первая из них — 90° — это прямой угол, знакомый еще из курса средней школы. Его вы точно не забудете. Остальные углы отличаются друг от друга на эти же самые 90°. Взгляните: 180°; 270°; 360°. Таким образом, даже если вы забудете эти числа, их всегда можно восстановить, если просто запомнить, что прямой угол — это 90°. А теперь разберем конкретные примеры. Будем учиться искать координатные четверти быстро, поскольку от этого умения напрямую зависит решение задачи B11.
Для начала переведем все углы из радиан в градусы по правилу: А затем найдем координатную четверть, ориентируясь по границам: 90°, 180°, 270°, 360°. Имеем:
Как видите, далеко не всегда можно найти значение самой тригонометрической функции. Например, попробуйте вычислить cos 162° или sin 108°. Зато мы всегда можем определить, в какой координатной четверти находится данный угол. Видео:Изобразить на единичной окружности точку.Скачать  Нестандартные углы и периодичностьДо сих пор мы рассматривали Но что произойдет, если, например, А как насчет отрицательных углов? Такие углы редко встречаются на ЕГЭ по математике (по крайней мере, в части B), но лучше застраховать себя от подобных «неожиданностей», поэтому предлагаю разобрать и такие задачи. Тем более, схема решения практически ничем не отличается от «стандартных» углов. Итак, что если Судя по тригонометрической окружности, точка сделает полный оборот — а затем пройдет еще чуть-чуть. Это самое «чуть-чуть» вычисляется очень просто. Достаточно отнять от исходного угла величину 360° (иногда это приходится делать несколько раз). С отрицательными углами работаем аналогично. Если добавлять к отрицательному углу величину 360°, мы очень скоро получим новый угол Таким образом, вся схема решения выглядит следующим образом:
Снова переводим все углы из радиан в градусы по правилу: Дальше уменьшаем или увеличиваем аргумент на 360° до тех пор, пока он не окажется на отрезке И только затем выясняем координатную четверть. Получим:
Вот и все! Обратите внимание: во втором пункте пришлось вычитать 360° три раза — и только затем получился нормальный угол. Аналогично, в четвертом пункте пришлось прибавлять два раза по 360°, чтобы выйти на положительный угол. Таким образом, добавлять и вычитать углы иногда приходится много раз — это не должно настораживать. В заключение хочу добавить, что если вы хорошо знаете математику и быстро ориентируетесь в радианных углах, то совсем необязательно переводить их в градусы. Однако большинство людей (и не только школьники) предпочитают именно градусную меру — знакомую еще со средней школы и, как следствие, более понятную. 📹 ВидеоЗнаки синуса, косинуса, тангенса ЛекцияСкачать  Алгебра 10 класс. 15 сентября. Числовая окружность #1Скачать  3 четверть. 9 класс. Алгебра. Углы на единичной окружностиСкачать 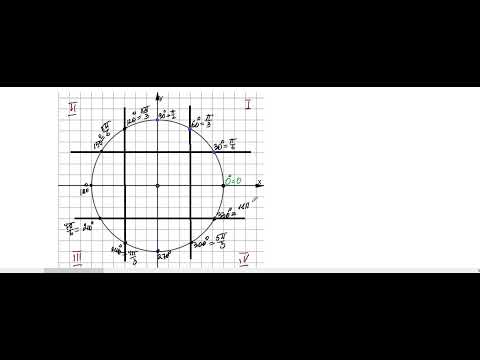 |