Как построить вектор по координатам точек (8 видео)

Нахождение координат вектора через координаты точек

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

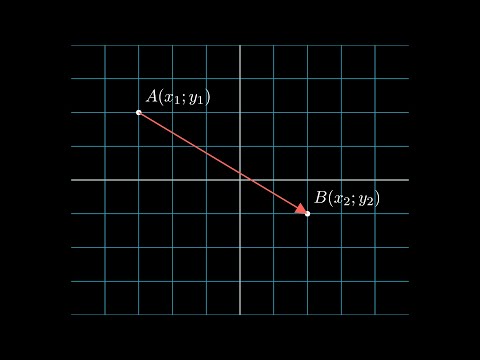
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Содержание

Векторы в пространстве и метод координат
Система координат в пространстве
Плоскость в пространстве задается уравнением:
Геометрия
Разложение векторов
Координаты векторов
Сложение и вычитание векторов
Признак коллинеарности векторов
📹 Видео

Видео:Координаты вектора. 9 класс.Скачать

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Видео:Координаты точки и координаты вектора 1.Скачать

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Видео:Как построить точки в системе координат OXYZСкачать

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Видео:9 класс, 2 урок, Координаты вектораСкачать

Геометрия

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Разложение векторов

Заметим, что если два вектора a и b коллинеарны, то обязательно найдется такое число k, для которого будет справедливо равенство:

Длина а составляет 6 клеток, а длина b – 9 клеток, при этом они сонаправлены. Получается, что b длиннее a в 9/6 = 1,5 раза, а потому можно записать:

Мы смогли выразить b через а. Иначе можно сказать, что мы разложили вектор b по вектору a. Можно и наоборот, выразить b через a:

Теперь посмотрим на вектора с и d. Их длины составляют 4 и 8 клеток, то есть отличаются в 2 раза, при этом они противоположно направлены. Поэтому эти вектора можно выразить так:

Обратите внимание, что выразить, например, а через с не удастся. Действительно, предположим, что есть такое число k, что

Тогда, по определению операции умножения вектора на число, вектора а и c должны быть коллинеарными, но они таковыми не являются.

Вектор можно раскладывать не на один, а на два вектора, которые ему не коллинеарны. Покажем это на примере:

Здесь вектора р, а и b не коллинеарны, при этом р выражен через а и b:

В данном случае говорят, что р разложен на вектора а и b, а числа 2 и 4 именуют коэффициентами разложения.

Верно следующее утверждение:

Продемонстрируем, как можно осуществить такое разложение. Пусть заданы вектора с, а и b, и требуется разложить c на а и b:

На первом шаге просто отложим все три вектора от одной точки. Далее построим прямые, проходящие через вектора а и b:

Далее через конец вектора с проведем прямые, параллельные построенным на предыдущем шаге прямым. В результате у нас получится некоторый параллелограмм АВСD:

Заметим, что вектор с оказался диагональю в этом параллелограмме. Тогда, согласно правилу параллелограмма, можно записать:

Ясно, что вектора АВ и b коллинеарны, так как лежат на одной и той же прямой. Тогда найдется такое число k, для которого будет верно отношение:

Конкретно в данном случае видно по рисунку, что АВ вдвое длиннее вектора b, поэтому

Аналогично коллинеарными являются вектора а и АD, поэтому существует число m, при котором справедливо равенство:

Понятно, что числа k и m определяются единственным образом. В общем случае они могут быть не только целыми, но и дробными (в том числе иррациональными) и даже отрицательными числами. Проще говоря, они могут быть любыми действительными числами.

Задание. Найдите коэффициенты разложения вектора d на вектора e и f:

Решение. Отложим все три вектора от одной точки. Далее проведем прямые, на которых лежат вектора e и f:

Теперь через конец d проводим ещё две прямые, параллельные двум уже построенным прямым, и в результате получаем параллелограмм:

Вектор d можно представить в виде суммы:

Особняком стоит случай, когда раскладываемый вектор коллинеарен одному из тех векторов, на которые он раскладывается. В этом случае один из коэффициентов разложения оказывается равным нулю. Например, пусть с надо разложить на а и b:

Строить параллелограмм в данном случае не нужно. Так как а и с коллинеарны, то найдется некоторое число k, при котором будет выполняться равенство:

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Координаты векторов

Из курса алгебры нам известна прямоугольная система координат. В ней есть оси Ох и Оу, а каждая отмеченная на плоскости точка имеет свои координаты:

Естественно, что на координатной плоскости можно отметить и вектора. Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направление которых совпадает с направлениями осей координат. Тот вектор, который лежит на оси Ох, обозначают буквой i, а тот, который лежит на оси Оу, обозначают как j.

Эти вектора называют единичными векторами, или ортами (ещё используется термин координатный вектор). Они не коллинеарны друг другу, а это означает, что любой вектор на плоскости можно разложить на единичные вектора. Коэффициенты такого разложения как раз и являются координатами вектора.

Посмотрим на примере, как находить координаты вектора. Пусть задан вектор а:

Нам надо разложить а по векторам i и j. Для этого их следует отложить от одной точки. Удобно перенести вектор а к началу координат:

Теперь надо через конец а провести прямые, параллельные векторам iи j. В результате получится прямоугольник АВСD:

Можно записать равенство:

Значит, и координаты данного вектора – это числа 3 и 2. Записывается это так:

Обратите внимание, что порядок чисел в скобках принципиально важен. Первое число – это коэффициент разложения, стоящий перед вектором i. Эту координату можно называть координатой х (по аналогии с координатами точек). Второе число – это коэффициент при векторе j, оно является координатой у. Также заметим очевидный факт, что координаты равных векторов одинаковы.

В приведенном выше примере легко заметить, что после того, как мы перенесли вектор в начало координат, координаты его конца (он обозначен точкой С) совпали с координатами самого вектора. Действительно, точка С имеет координаты (3; 2).

Это правильно несколько упрощает определение координат вектора. Достаточно просто отложить вектор от точки начала координат, после чего посмотреть на координаты его конечной точки. Отметим, что вектор, чье начало совпадает с началом координат, имеет особое название – радиус-вектор.

Задание. Определите координаты векторов a, b, c и d, отмеченных на рисунке:

Решение. Во всех случаях будем просто переносить вектора к началу координат, получая радиус вектора. Далее будем просто смотреть, каковы координаты конца радиус-вектора. Начнем с а:

После переноса а его конец оказался в точке А(4; 3), поэтому и координаты всего вектора можно записать так:

После переноса вершина радиус-вектора попала в точку B (1; – 3), поэтому вектор имеет координаты .

Выполним построение и для с:

Конец вектора попал в точку С (3,5; 0), а потому и координаты вектора составляют .

Осталось рассмотреть d:

Здесь координаты вектора будут равны , так как такие же координаты имеет точка D.

Рассмотрим решение обратной задачи, в которой необходимо построить вектор по заранее заданным координатам.

Задание. Даны координаты вектора:

Постройте по три вектора, имеющие заданные координаты.

Решение. Проще всего построить радиус-вектор, вершина которого будет иметь те же координаты, что и требуемый вектор:

Чтобы построить ещё два вектора с такими же координатами, надо просто отложить уже построенный вектор от любых других точек:

Аналогично поступаем и во второй задаче – сначала откладываем радиус-вектор с заданными координатами, а потом добавляем ещё два равных ему вектора, отложенных от других точек:

Отдельно отметим нулевой вектор. Очевидно, что все его координаты равны нулю, так как для него можно записать такое разложение на орты:

Также можно сказать, что если отложить нулевой вектор от начала координат, то его конец также будет находиться в начале координат (так как у нулевого вектора начало и конец совпадают), то есть в точке с координатами (0; 0).

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сложение и вычитание векторов

Пусть у нас есть векторы a<x₁; у₁> и b<x₂; у₂>. Можно ли, зная только их координаты, определить их сумму и разность? Оказывается, можно. Действительно, по определению координат векторов (напомним, они являются коэффициентами разложения вектора на орты) можно записать:

Эта запись означает, что с имеет координаты <х₁ + х₂; у₁ + у₂>. В результате мы можем сформулировать правило сложения векторов:

Проиллюстрируем правило на примере. Пусть надо сложить вектора а и b . Понятно, что в результате получится новый вектор, который мы обозначим как с . Чтобы найти его первую координату, надо сложить первые координаты векторов a и b:

Для нахождения второй координаты складываем соответственно вторые координаты векторов:

В итоге получился вектор с .

Задание. Сложите вектора, имеющие координаты:

Решение. Сначала просто складываем первые числа в скобках (и получаем координату х), а потом – вторые (и получаем координату у):

Теперь попытаемся понять, как вычислять разность двух векторов. Пусть есть вектора с заранее заданными координатами a<x₁; у₁> и b<x₂; у₂>. Снова запишем их разложение на единичные вектора:

Теперь мы можем сформулировать правило вычитания векторов:

Например, пусть надо вычесть из вектора а вектор b. Искомая разность будет представлять собой вектор, чья координата х будет равна разности первых координат векторов а и b:

Аналогично вычисляем и координату у:

В итоге получили вектор с координатами .

Задание. Вычтите из вектора а вектор b, если известны их координаты:

Решение. Во всех случаях мы сначала из первой координаты вектора а вычитаем первую координату b, в результате чего получаем координату х искомого вектора. Далее повторяем процесс со второй координатой (то есть с у):

Далее рассмотрим такую операцию, как умножение вектора на число. Снова запишем, что вектор а с координатами х₁и у₁ можно разложить на орты следующим образом:

Это означает, что при умножении вектора на число надо просто умножить на это число каждую его координату.

Например, есть вектор а, который надо умножить на 5. Умножим на 5 по отдельности каждую координату:

В результате получился вектор .

Задание. Умножьте вектор а на число k, если известно, что:

Решение. Надо всего лишь умножить каждую координату а на число k, и таким образом получить новые координаты:

Видео:11 класс, 2 урок, Координаты вектораСкачать

Признак коллинеарности векторов

Напомним, что если два вектора (обозначим их как a и b) коллинеарны, то обязательно существует такое число k, что

Из равенства (1) и рассмотренного нами правила умножения вектора на число вытекают два соотношения между этими координатами:

Если числа х₂ и у₂ не равны нулю, то можно выразить из каждого уравнения число k, после чего выражения можно будет приравнять:

Получили соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратную сторону – если координаты векторов удовлетворяют выведенному отношению, то можно смело утверждать, что вектора – коллинеарны.

Примечание. Формулировка «тогда и только тогда» означает, что правило действует в обе стороны – из пропорциональности координат следует коллинеарность векторов, а из коллинеарности векторов следует пропорциональность координат.

Покажем, как пользоваться этим признаком коллинеарности векторов. Пусть вектор а имеет координаты , а у вектора b они равны . Нам надо определить, коллинеарны ли они. Для этого поделим друг на друга их координаты х:

Получили число 3. Далее поделим и координаты у:

Снова получили тройку. То, что в обоих случаях получилось одно и тоже число, указывает на то, что вектора коллинеарны. Более того, можно даже записать, что вектор b втрое больше a:

В данном примере мы делили координаты второго вектора b на координаты первого вектора a. Но можно было поступить и наоборот, делить координаты а на координаты b:

Естественно, снова получилось одинаковое число.

Особняком стоит случай, когда одна из координат вектора равна нулю. Например, пусть вектор имеет координаты <0; у₁>, причем у₁≠ 0. Любой коллинеарный ему вектор можно получить, умножив вектор на какое-то число k. В этом случае его координаты <x₂; у₂> составят:

Получается, что и у коллинеарного вектора координата х обязательно будет равняться нулю. В свою очередь координаты у₂ и у₁ могут быть любыми, ведь мы всегда можем найти такое число k, для которого будет выполняться условие

Например, есть вектор . Можно сказать, что ему будет коллинеарен любой вектор, у которого первая координата также равна нулю, в частности,

Но любой вектор, у которого координата х НЕ равна нулю, НЕ будет коллинеарен вектору . В частности, ему не будут коллинеарны вектора:

Аналогичная логика действует и тогда, когда нулю равна не координата х, а координата у.

Если же у вектора обе координаты равны нулю, то он является нулевым вектором, то есть точкой. Напомним, что такой вектор считается коллинеарным любому другому вектору.

Задание. Определите, являются ли коллинеарными два вектора, если их координаты равны:

Решение. В первых пяти случаях все координаты – ненулевые, а поэтому надо просто проверить их пропорциональность. Для этого надо делить координаты друг на друга:

Числа различны, поэтому вектора НЕ коллинеарны.

В следующих примерах как минимум одна из координат равна нулю, поэтому делить координаты уже не нужно.

У обоих векторов координаты х нулевые, этого достаточно, чтобы утверждать, что они коллинеарны.

У первого вектора координата х – нулевая, в то время как у второго нет. Значит, они не коллинеарны.

Здесь у первого вектора нулю равна координата х, а у второго она ненулевая, поэтому вектора не коллинеарны.

Здесь имеет место особый случай, ведь первый вектор – нулевой, то есть представляющий собой точку. Считается, что он коллинеарен любому вектору, поэтому в данном примере вектора коллинеарны.

Ответ: а) да; б) нет; в) да; г) да; д) нет; е) да; ж) нет; з) да; и) нет; к) да.

Пока что мы рассматривали задачи, в которых фигурируют только вектора. Однако в будущем мы научимся с помощью метода координат решать и другие задачи, в которых рассматриваются отрезки, треугольники, окружности и прочие геометрические фигуры.