Как построить окружность с радиусом корень (6 видео)

Как построить окружность?

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
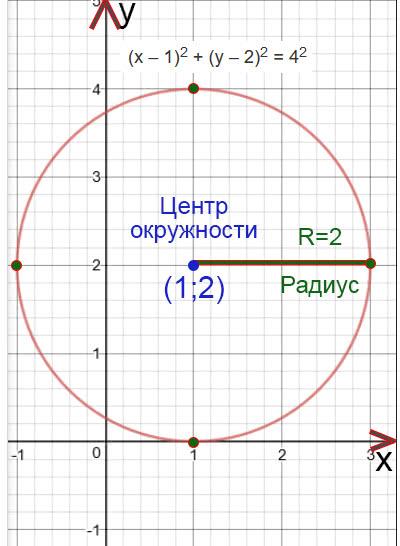
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Содержание

Окружность радиуса корень из 3
Задача 29507 9.7. Окружность радиуса sqrt(3).
Условие
Решение
Окружность радиуса корень из 3
Как написать хороший ответ?
Философская геометрия, Часть 2. Корень из трех и его практическое применение
Круг. Окружность (центр, радиус, диаметр)
🔍 Видео

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Окружность радиуса корень из 3

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Задача 29507 9.7. Окружность радиуса sqrt(3).

Условие

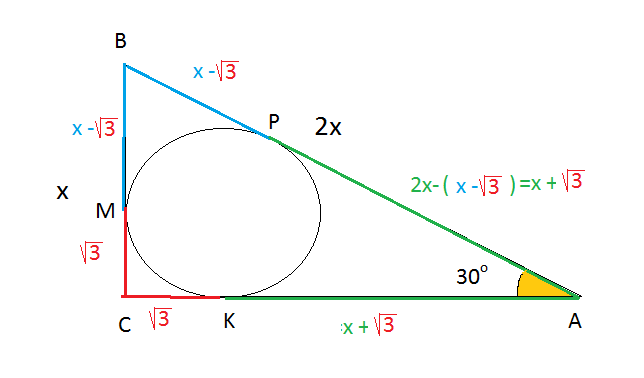
9.7. Окружность радиуса sqrt(3), вписанная в прямоугольный треугольник АВС с углом угол A = 30° , касается катета АС в точке К. Найдите ВК

Решение

В прямоугольном треугольнике против угла в 30 градусов лежит катет, равный половине гипотенузы.

Пусть АВ=2х, тогда ВС=х

По свойству касательных к окружности, проведенных из одной точки, отрезки касательных равны.

Значит,
АС=sqrt(3) + (x+sqrt(3))=x+2sqrt(3)

По теореме Пифагора из прямоугольного треугольника АВС
AB^2=AC^2+BC^2

x_(1)=(2sqrt(3)+6)/2 = sqrt(3) +3

x_(2)=(2sqrt(3)-6)/2

Видео:Тригонометрическая окружность. Как выучить?Скачать

Окружность радиуса корень из 3

Вопрос по геометрии:

В равнобедренный треугольник вписана окружность радиуса корень из 3.Угол при основании 60 градусов.Найти основание.

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 2

Если угол при основании равен 60, то противоположный угол будет равен тоже 60, следовательно и угол при вершине равен 60. получается равно стороний треугольник. По формуле радиуса в равновносторонем треугольнике найдём его сторону. , где а — сторона треугольника.

так как это равностороний треугольник, то все стороны будут равны 6 и основание тоже.

извините за кривую окружность)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Философская геометрия, Часть 2. Корень из трех и его практическое применение

Сейчас я вам что покажу, закачаетесь. Обязательно загляните под кат, самые интересные картинки я припрятал там.

Я продолжаю рассказ о применении философской геометрии на практике. Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.

Сегодня я расскажу про замечательную пропорцию «корень из трех». Я покажу ее сакральный смысл, а под катом продемонстрирую пример из современного дизайна, который повергнет вас в шок 😉

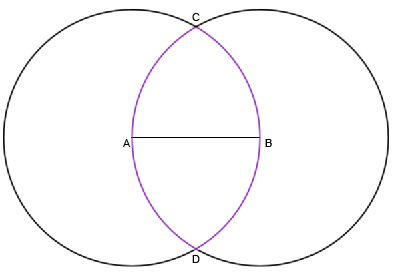
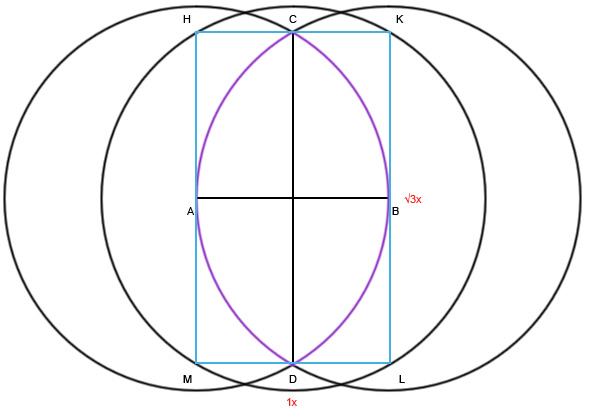
Начнем с построения пропорции. Возьмем отрезок AB.

Примем его за радиус и построим окружность с центром в A.

Теперь построим вторую окружность с тем же радиусом, но с центром в B.

У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример — она давно является символом христианства.

Я продолжу под катом. Спорим, никогда не догадаетесь чем там все закончится 🙂

Ну вот, раз мы уже под катом, начну сыпать картинки. Мы остановились на Vescica Piscis и символе христианства. Вот Христос вписан в эту фигуру.

Вот здесь изображено много символической рыбы.

Кстати, впервые я про это узнал, купив вот такую подвеску в Кафедральном соборе Уппсалы. Так что символ вполне используется и сейчас.

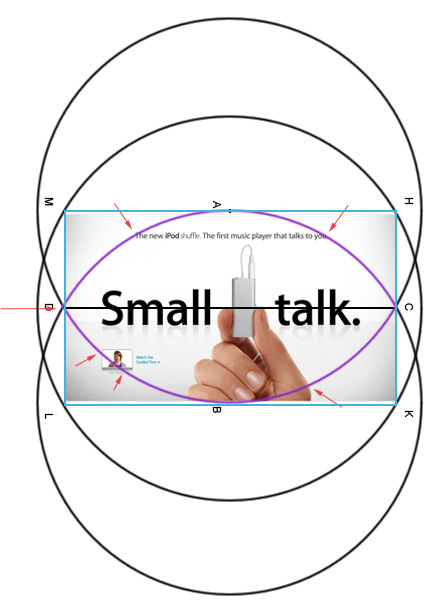
Но чем же так примечательна фигура? Давайте вернемся к построениям. Соединим точки C и D, а из места их пересечения нарисуем еще одну окружность с радиусом AB. Нарисуем прямоугольник HKLM.

Этот прямоугольник обладает замечательным свойством. Его высота относится к ширине ровно как корень их трех (√3 / 1). Корень из трех — это одно из основных иррациональных чисел, но основе которых строилось множество картин, зданий и просто предметов.

Но если вы думаете, что это все старо, уныло и протухло, то вы ошибаетесь. Я обещал сюрприз. Готовы? Только громко не смейтесь.

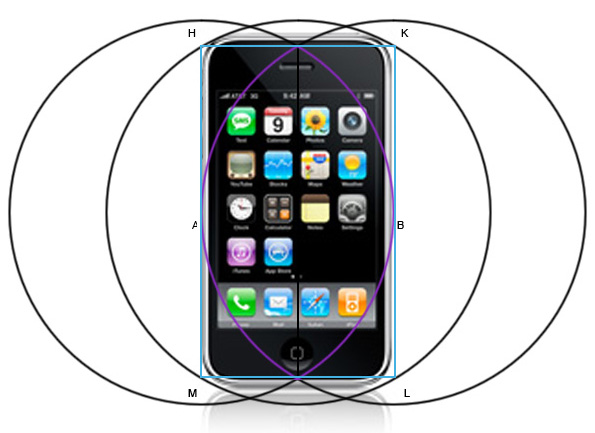
Да-да, это он. iPhone не идеально помещается в этот прямоугольник, но его размеры чрезвычайно близки. Мне кажется что это не совпадение вот почему.
Корень из трех — это примерно 1.732050…
Отношение сторон айфона первого поколения (115×61) примерно равно 1.88524.
iPhone 3G (115.5×61.8) — 1.8599
iPod Touch (110×61.8) — 1.779

Смотрите, они стремятся к идеалу! Мешать им могут только тысячи технических причин.

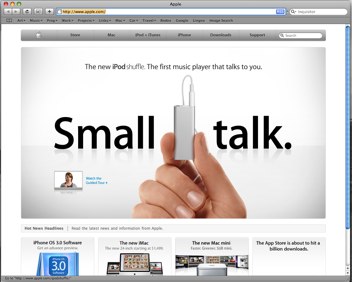
Удивлены? Смущены? Не верите? Сейчас будет больше. Зайдем на apple.com

Хм… Что-то мне этот центральный блок напоминает. А ну ка…

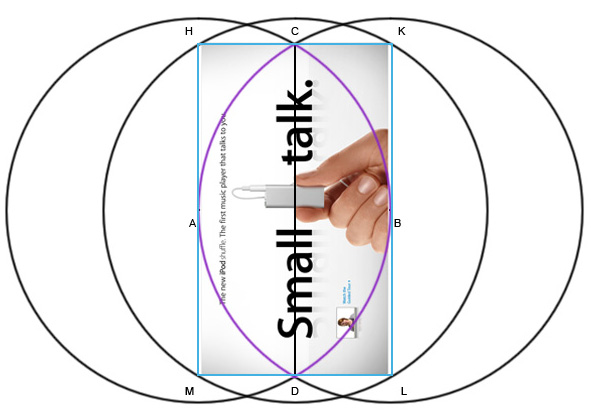
Ага! Вот вы и попались. Давайте ка посмотрим поближе.

Обратите внимание как потрясающе дизайны Apple используют эту разметочную сетку. Этому геометрическому построению я даже не знаю сколько сотен лет. Оно использовалось в иконах, храмах, скульптурах. Современные дизайнеры мастерски используют его в обычных коммерческих вещах и оно продолжает безотказно работать. Их вещи покупают вопреки всякому смыслу.

Что же это мистика? Расчет? Геометрия? Философия? Нам остается только практиковаться и пытаться узнать это самим

Видео:Отбор корней по окружностиСкачать

Круг. Окружность (центр, радиус, диаметр)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.