Корзина

Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,













Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».
Теоретический урок для решения задач по теме «Решение треугольников». Бесплатное обучение.
Содержание данной онлайн страницы электронного справочника по предмету математики для школьников:
- – задачи 76 — 77 представлены с примерами решений и ответами;
- – онлайн задания, как найти решение треугольника через синус и косинус угла, рассматриваются в тестах 78 — 81;
- – решения, как найти угол, сторону треугольника, объясняются на данном уроке в контрольных работах 82 — 85.
Задача 76.


стороны треугольника a=10, b=7
Угол 

Решить треугольник: Угол по сторонам треугольника 




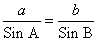
Sin B = 
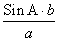

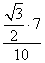

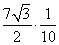

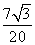
Используя Sin B ≈ 0,6062, находим из тригонометрической таблицы («Четырехзначные математические таблицы» Владимира Модестовича Брадиса)


Тогда 

Используя теорему синусов

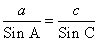

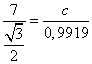



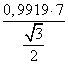
Ответ: 



Задача 77.
Треугольник ΔABC, стороны треугольника




Найти: Угол по сторонам треугольника 



Т.к. a=b=6,3, то треугольник ΔABC — равнобедренный.
Тогда 



Используя теорему синусов

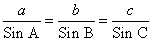

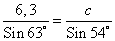



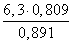

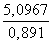
Ответ: 



Видео:9 класс. Геометрия. Решение треугольниковСкачать

Решение треугольников через синус и косинус угла
Задача 78.






Найти: угол треугольника 



Используя теорему синусов

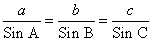

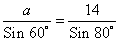



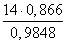

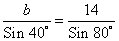



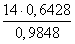
Ответ: 

Задача 79.


Найти: углы треугольника 






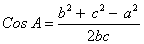
Cos B = 
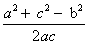

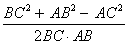

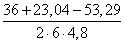

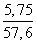
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла B


Используя формулу теоремы косинусов, находим косинус угла C
Cos C = 
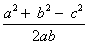

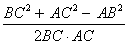
= 
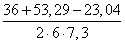
Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим значение угла C


Тогда угол A равен 

Ответ: 





Задача 80.




Найти: угол 



Т.к. два угла в треугольнике равны 



Значит, две стороны равны AC=AB=b=c=4,5
Используя теорему синусов

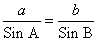
находим сторону BC=a





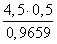
Ответ: 

Задача 81.
Треугольник ΔABC, длины трех его сторон
| 1) a=5 , b=c=4 Найти: является ли треугольник тупоугольным, прямоугольным, остроугольным 1) Т.к. b=c=4, то треугольник ΔABC — равнобедренный, и, значит, остроугольный. Cos A = Тогда угол A равен 3) Используя формулу теоремы косинусов Cos B = Треугольник ΔABC, два угла и сторона Найти: длину всех сторон треугольника ΔABC = ? Зная размер двух углов в треугольнике ΔABC, находим третий угол Найдем угол Используя теорему синусов AC = (3 • 1) • 2 = 6 (м) Используя теорему синусов AB = Используя теорему синусов Ответ: AB ≈ 3 м, AC = 6 м, BC ≈ 4 м. Три стороны a = 14, b = 18, все углы треугольника ΔABC = ? Т.к. против большего угла лежит большая сторона, то используя формулу теоремы косинусов Cos C = Cos C = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C Используя формулу теоремы косинусов Cos B = Cos B = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла B Следовательно, Ответ: Задача 84. Треугольник ΔEKP, сторона и два угла Найти: сторону треугольника PK = ? Используя теорему синусов Sin 115° = Sin (180° — 65°) = Sin 65° Тогда Задача 85. Треугольник ΔABC, две стороны и угол Найти: решить треугольник — определить значение стороны и двух углов (a, Используя формулу теоремы косинусов a = Используя формулу теоремы косинусов Cos C = Cos C = Используя тригонометрические таблицы («Четырехзначные математические таблицы» В. М. Брадиса), находим приближенное значение угла C Следовательно, Ответ: a ≈ 13,8 ; Видео:9 класс, 15 урок, Решение треугольниковСкачать  Методический сборник «Решение треугольников», 9 классОбращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов Сертификат и скидка на обучение каждому участнику Методический сборник по геометрии «Решение треугольников», 9 класс обобщить и систематизировать изученное на предыдущих уроках; научить учащихся решать задачи на использование теоремы синусов и теоремы косинусов(задачи подобраны для табличных углов); повторить методы решения прямоугольных треугольников, познакомить учащихся с основными алгоритмами решения произвольных треугольников; проконтролировать степень усвоения материала; продолжить работу по развитию мыслительной деятельности – выделять главное, ставить и разрешать проблемы, сравнивать и строить аналогии; способствовать развитию логического мышления учащихся;воспитание интереса к предмету. Оборудование:- учебник АтанасянаЛ.С «.Геометрия 7-9», классы, издательство Дрофа, Сборник Ершова и Голобородько «Самостоятельные и контрольные работы. Алгебра и геометрия», 9 класс, сборник Алтынов П.И. Тесты. Геометрия 7-9. Формы организации учебной деятельности: фронтальная, индивидуальная, парная, коллективная. Методы обучения: словесные, частично-поисковые, практические, наглядные, самостоятельной. Урок 1 Тема «Синус, косинус и тангенс угла. Площадь треугольника. 1.Актуализация опорных знаний. Вспомнить определение синуса, косинуса и тангенса угла. Основное тригонометрическое тождество, формулы приведения. Выполнить №1012-1016(1). 2.Формирование новых знаний. Формулировка и доказательств формулы площади треугольника 3. Закрепление знаний, формирование умений. Устно. Формулы для вычисления площадей треугольников, значения тригонометрических функций табличных углов. 5.Домашнее задание №1. Урок 2. Теорема синусов и теорема косинусов. 1.Актуализация опорных знаний. Устно. Площади треугольник, параллелограмма и ромба. , , 1человек у доски. Доказать теорему синусов. 2.Формирование новых знаний. 1. Формулировка и доказательство теоремы косинусов. 2.Таблица Брадиса. Знакомство( в дальнейшем будем работать с табличными углами 30,45,60, 120,150 градусов) 3. Закрепление знаний, формирование умений. Задача. В треугольнике АВС АС=20, угол А равен углу С и равны по 30, угол В равен 120. Найти ВС. Решить задачу двумя способами. Формулировки теоремы синусов и косинусов, формулы приведения. 5. Домашнее задание №2. 1.В треугольнике АВС АВ= 6см, АС= 8 см, Угол А= 60. Найти S треугольника. 2.Две стороны треугольника равны 7см и см, а угол, противолежащий большей из них , равен 45.Найти другие углы треугольника. 3.В треугольнике две стороны равны 5 см и 16 см, а угол между ними 120 Найти третью сторону Урок 3. Решение треугольников. 1.Актуализация опорных знаний. 1)Устно : теоремы и формулы для нахождения площадей фигур. 2) Из домашнего задания задачи 2 и 3 на доске выполняют 2 человека. 2. Закрепление знаний, формирование умений. Задача 1. В треугольнике АВС угол АВС=120, АВ=6, площадь треугольника равна . Найти ВС. Задача 2. В параллелограмме АВСД ВС=, угол ВАД=30, ВД=ВС. Найти площадь параллелограмма. Задача 3. В прямоугольном треугольнике АВС угол С=90, СД – биссектриса, угол А=15, АС=. Задача 4 Найти сторону треугольника , лежащую против угла в 135, если две другие стороны и 3. Задача 5 ( дополнительно) В остроугольном треугольнике АВС ВД перпендикулярно АС, уголА=, угол В=, ВД=h. Найти АС. 3.Домашнее задание №3 1.В треугольнике АВС угол А=45, угол С=15, ВС = 4. Найти АС 2. В равнобедренном треугольнике АВС (АВ=ВС) .Угол А = , АС = в, АЕ – биссектриса. Найти АЕ 3. В равнобедренном треугольнике АВС угол при вершине В равен 120, АС = 2.Найти медиану АМ Урок 4 Решение треугольников. 1.Актуализация опорных знаний. Проверка дз. Задача 1- 2 человека у доски, задача 2- 1ч по желанию, задача 3 – 1 ч по желанию. Класс самостоятельно . Задача. В треугольнике АВС угол А=45, угол В=120. Найти АС, если ВС=12. 2.Формирование новых знаний. 3. Закрепление знаний, формирование умений. Задача 1. В треугольнике АВС АВ=18см, =6. Найти угол, противолежащий стороне АВ. Сколько решений имеет задача? Задача 2 № 1031 (а,б) 1.В треугольнике АВС угол А=45, угол В=60. Найти сторону ВС. 2.В параллелограмме АВСД АВ=7, АД=17, угол А=45. Найти сторону АС и площадь параллелограмма. 3. В треугольнике АВС АВ=20, ВС=10, угол В=30. Найти АС, угол А, угол С. 1.В треугольнике АВС угол А=60 АВ=3, ВС=3. Найти угол С. 2.В параллелограмме АВСД АВ=3, АД=11, угол В=150. Найти диагональ ВД и площадь параллелограмма. 3. В треугольнике АВС АС=7, ВС=4, угол С=45. Найти АВ, синус угла А, синус угла В. 5.Домашнее задание №4 2.Диаметр окружности равен 12 см, а сторона вписанного треугольника равна 6см. Найти угол, противолежащий данной стороне. Сколько решений имеет задача? 3.В параллелограмме стороны равны 4 и 5см, острый угол равен 45. Найти диагонали и площадь параллелограмма Урок 5. Решение треугольников. 1.Актуализация опорных знаний. 1)Устно. Определение синуса, косинуса, значения тригонометрических функций табличных углов и 120, 135и 150 градусов: нахождение синуса, если дан косинус 2)Из дз № 1031(в)- 1 человек у доски, задача 2-1человек, задача 3 – 1 человек. 3) Класс в это время : Задача В треугольнике АВС угол А=, угол В=, а радиус описанной окружности равен . Найти стороны треугольника и его площадь. 2. Закрепление знаний, формирование умений. Задача 1. В треугольнике АВМ АВ = 4, ВМ = 8, АМ = 10. С-середина АМ, К – середина ВМ. Найти косинус угла ВСК. Задача 2. Две стороны треугольника 4 и 7 см, а косинус угла между ними равен . Определить синусы всех углов треугольника и его третью сторону. 3.Домашнее задание №5 1Стороны треугольника равны 7, 37 и 40 см. Найти угол, противолежащий средней стороне треугольника. 2.Решите треугольник АВС, если ВС = 5, АС = 7 см, угол С = 135 Урок 6. Решение треугольников. 1.Проверка опорных знаний. Решение задач 1-6 из теста «Теоремы синусов и теоремы косинусов»( сборник Алтынов П.И. Тесты. Геометрия 7-9 классы, издательство Дрофа) 5.Домашнее задание №6 2. В треугольнике две стороны равны 5 и 12 см, а косинус угла между ними равен . Найти а) третью сторону, б) площадь треугольника, в) синус большего угла , в) радиус описанной около треугольника. Урок 7. Решение треугольников. 1.Актуализация опорных знаний. 1)Итоги выполнения теста 3) задача 8 из теста 1 варианта. АВСД – трапеция(смотри рисунок). АВ = 4 см, ВС=2см, угол В=120, диагональ АС перпендикулярна СД. Найти основание АД. 2. Проверка опорных знаний .Самостоятельная работа. Сборник Ершова и Голобородько,С-6. Теорема о площади треугольника. Теорема синусов.( 2 задачи). 2. Домашнее задание №7 1. В треугольнике АВС АС = 5, ВС = 6, cosC =. Найти площадь треугольника, сторону АВ, синус меньшего угла и радиус описанной окружности. Урок 8. Решение треугольников. 1.Актуализация опорных знаний. 1) выборочная проверка дз 2) устно :формулы для нахождения площадей, теоремы синусов и косинусов, как найти R , диагонали в параллелограмме, если известны стороны и угол 2. Закрепление знаний и умений. Задача 1 Две стороны треугольника 3 и 7см, а угол, противолежащий большей из них равен 60.Найти третью сторону. Доказать, что угол, противолежащий третьей стороне – тупой. Задача 2. В параллелограмме биссектриса тупого угла, равного 120, делит сторону параллелограмма на отрезки, равные 15 см и 10 см, начиная от вершины острого угла. Найти биссектрису и большую диагональ параллелограмма. 3. Проверка опорных знаний .Самостоятельная работа СА-7. Теорема косинусов. Решение треугольников. 5. Домашнее задание №8 1. В треугольнике две стороны равны 5 и 7 см, а угол, противолежащий большей из них, равен 60 . Найти третью сторону и доказать, что угол, противолежащий третьей стороне — острый . 2. В параллелограмме биссектриса острого угла , равного 60, делит сторону параллелограмма на отрезки 25 и 15 см, начиная от вершины тупого угла. Найти биссектрису и меньшую диагональ Урок 9. Контрольная работа. «Решение треугольников» 1.Диагонали параллелограмма равны 12 см и 20 см, а угол между ними 60. Найти стороны параллелограмма. 2.Дан треугольник АВС, угол А=45, угол В=75, АВ = 2 см. Найти : угол С и сторону ВС. 3. В треугольнике АВС ВА = 6 см, АС = 8 см, а его площадь 12 . Найти синус угла А, градусную меру угла А, если известно, что угол А – тупой. 4. Стороны треугольника 3см, 5 см и 7 см. Найти угол треугольника, противолежащий стороне, равной 7 см. 5.Дополнительно. В прямоугольном треугольнике один из углов равен a . Выразить через и а биссектрису прямого угла треугольника. 1.Стороны параллелограмма равны 10 см и 16 см, а угол между ними 60. Найти диагонали параллелограмма. 2.Дан треугольник АВС, угол С=105, угол В=30, АС = 4 см. Найти : угол А и сторону ВС. 3. В треугольнике КМР КМ = 4 см, МР = 5 см, а его площадь 5 . Найти синус угла М, градусную меру угла М, если известно, что угол М – тупой. 4. Стороны треугольника 3см, 8 см и 7 см. Найти угол треугольника, противолежащий стороне, равной 7 см. 5.Дополнительно. В прямоугольном треугольнике гипотенуза равна с, один из острых углов равен . Выразить через с и биссектрису второго острого угла треугольника. 5. Домашнее задание №9 Задача № 314907 (ОГЭ). Стороны АС, АВ, ВС треугольника АВС равны 3, и 1 соответственно. Точка К расположена вне треугольника АВС, причем отрезок КС пересекает сторону АВ в точке, отличной от В.Известно, что треугольник с вершинами К, А и С подобен исходному. Найдите косинус угла АКС, если угол КАС . Видео:ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать  Решение треугольников онлайнС помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже. Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°. Видео:РЕШЕНИЕ ТРЕУГОЛЬНИКОВ. Контрольная № 1 Геометрия 9 класс.Скачать  Решение треугольника по трем сторонамПусть известны три стороны треугольника a, b, c (Рис.1). Найдем
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Видео:Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать  Решение треугольника по двум сторонам и углу между нимиПусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:
Далее, из формулы
Далее из (3) с помощью калькулятора находим угол A. Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: Решение. Иcпользуя теорму косинусов найдем сторону c:
Из формулы (3) найдем cosA:
Поскольку уже нам известны два угла то находим третий:
Видео:№1025. С помощью теорем синусов и косинусов решите треугольник ABC, если:Скачать  Решение треугольника по стороне и любым двум угламПусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем: 📺 ВидеоПодобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать  Геометрия 9 класс (Урок№17 - Решение треугольников. Измерительные работы.)Скачать  Решение треугольников | Геометрия 7-9 класс #98 | ИнфоурокСкачать  Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать  Планиметрия | решение треугольников | 3Скачать  Треугольники. Практическая часть - решение задачи. 7 класс.Скачать  9 класс. Геометрия. Решение треугольников. Теорема косинусов. Теорема синусов. Урок #2Скачать  ЕГЭ. Математика. Решение треугольников. ПрактикаСкачать  9 класс, 13 урок, Теорема синусовСкачать  Таблица значений тригонометрических функций - как её запомнить!!!Скачать  Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать  урок 3 Решение треугольниковСкачать  первый признак равенства треугольников. Задачи по готовым чертежам, рисункам. 7 классСкачать  ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать  |


 2) Используя формулу теоремы косинусов
2) Используя формулу теоремы косинусов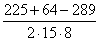 =
= 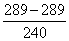 =0
=0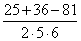 = —
= — 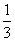
 Дано:
Дано: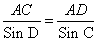 , находим сторону AC
, находим сторону AC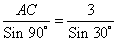
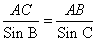 , находим сторону AB
, находим сторону AB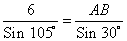
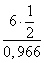 ≈ 3 (м)
≈ 3 (м)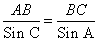 , находим сторону BC
, находим сторону BC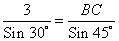
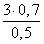 ≈ 4 (м)
≈ 4 (м)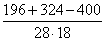 =
= 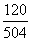 ≈ 0,24
≈ 0,24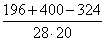 =
= 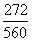 ≈ 0,4857
≈ 0,4857
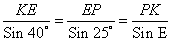 , находим сторону PK
, находим сторону PK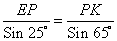
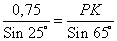
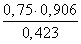 ≈ 1,61
≈ 1,61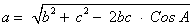 , получаем
, получаем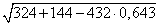 =
= 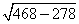 ≈ 13,8
≈ 13,8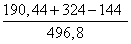 =
= 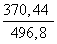 ≈ 0,7457
≈ 0,7457



 .
.




 .
. Найти
Найти 
 .
.
 .
. ,
,  .
.


 .
. .
. .
. и
и  (Рис.2). Найти сторону c и углы A и B.
(Рис.2). Найти сторону c и углы A и B.

 .
.

 .
.
 .
.
 .
. ,
,  .
. ,
,  .
. и углы
и углы  (Рис.3). Найти стороны b и c и угол С.
(Рис.3). Найти стороны b и c и угол С.


