Если соответственные углы в сумме дают 180 градусов то прямые параллельны (6 видео)

Признаки и свойства параллельных прямых

Содержание

Признаки параллельных прямых
Свойства параллельных прямых
Прямая линия. Признаки параллельности прямых линий.
Признаки параллельности прямых
Углы, образующиеся при пересечении двух прямых третьей прямой
Признаки параллельности двух прямых
🔍 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Признаки параллельных прямых

1. Если две прямые параллельны третьей прямой, то они являются параллельными:

2. Если две прямые перпендикулярны третьей прямой, то они параллельны:

Остальные признаки параллельности прямых основаны на углах, образующихся при пересечении двух прямых третьей.

3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны:

Если ∠1 + ∠2 = 180°, то a || b.

4. Если соответственные углы равны, то прямые параллельны:

5. Если внутренние накрест лежащие углы равны, то прямые параллельны:

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Свойства параллельных прямых

Утверждения, обратные признакам параллельности прямых, являются их свойствами. Они основаны на свойствах углов, образованных пересечением двух параллельных прямых третьей прямой.

1. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°:

Если a || b, то ∠1 + ∠2 = 180°.

2. При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны:

3. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы равны:

Следующее свойство является частным случаем для каждого предыдущего:

4. Если прямая на плоскости перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой:

Пятое свойство — это аксиома параллельности прямых:

5. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой:

Видео:Теорема 14.2 Если сумма односторонних углов равна 180 градусов, то прямые параллельны || Геометрия 7Скачать

Прямая линия. Признаки параллельности прямых линий.

Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:

соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

внутренние накрест лежащие углы: 3 и 5, 4 и 6;

внешние накрест лежащие углы: 1 и 7, 2 и 8;

внутренние односторонние углы: 3 и 6, 4 и 5;

внешние односторонние углы: 1 и 8, 2 и 7.

Описанные углы видны на рисунке:

Теорема.

Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:

1. внутренние накрест лежащие углы одинаковы;

2. внешние накрест лежащие углы одинаковы;

3. соответственные углы одинаковы;

4. сумма внутренних односторонних углов будет 2d = 180 0 ;

5. сумма внешних односторонних углов будет 2d = 180 0 ;

Данную теорему иллюстрирует рисунок:

Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.

1. ∠ 4 = ∠ 6 и ∠ 3 = ∠ 5;

2. ∠ 2 = ∠ 8 и ∠ 1 = ∠ 7;

3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8;

4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d;

5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.

1. Из середины E того отрезка прямой MN, который размещается между параллельными прямыми, прочертим на СD перпендикуляр EK и продолжим его до пересечения с AB в точке L. Так как перпендикуляр к одной из параллельных есть также и перпендикуляр к другой параллельной, то образовавшиеся при этом треугольники (заштрихованные на чертеже) — оба прямоугольные. Они одинаковы, потому что в них по равной гипотенузе и по одинаковому острому углу при точке E. Из равенства треугольников получаем, что внутренние накрест лежащие углы 4 и 6 одинаковы. Два прочих внутренних накрест лежащих угла 3 и 5 одинаковы, как дополнения до 2d к одинаковым углам 4 и 6 (как смежные с 4 и 6).

2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.

Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.

Следовательно, ∠ 2 =∠ 8.

3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.

4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.

5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.

Из выше доказанного обоснования получаем обратные теоремы.

Когда при пересечении двух прямых произвольной третьей прямой получим, что:

1. Внутренние накрест лежащие углы одинаковы;

или 2. Внешние накрест лежащие углы одинаковые;

или 3. Соответственные углы одинаковые;

или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;

или 5. Сумма внешних односторонних равна 2d = 180 0 ,

Видео:ГЕОМЕТРИЯ 7 класс : Соответственные, односторонние и накрест лежащие углыСкачать

Признаки параллельности прямых

При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.

Видео:7 класс, 29 урок, Теоремы об углах, образованных двумя параллельными прямыми и секущейСкачать

Углы, образующиеся при пересечении двух прямых третьей прямой

Рисунок	Определение углов
	Внутренние накрест лежащие углы
	Внутренние накрест лежащие углы
	Внешние накрест лежащие углы
	Внешние накрест лежащие углы
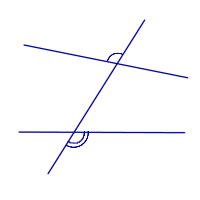	Соответственные углы



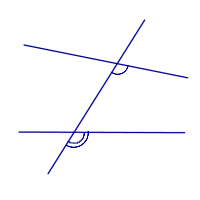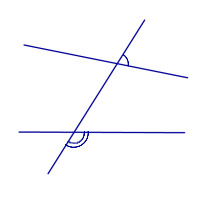
	Внутренние односторонние углы
	Внутренние односторонние углы
	Внешние односторонние углы
	Внешние односторонние углы

Внутренние накрест лежащие углы

Если соответственные углы в сумме дают 180 градусов то прямые параллельны

Внешние накрест лежащие углы

Соответственные углы

Внутренние односторонние углы

Внешние односторонние углы

Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.

Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.

Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.

Видео:Пары углов в геометрииСкачать

Признаки параллельности двух прямых

Рисунок	Признак параллельности
	Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны

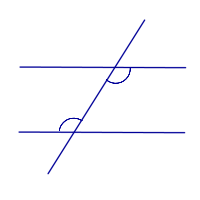	Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны

	Прямые параллельны тогда и только тогда, когда соответственные углы равны



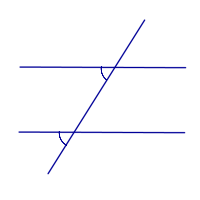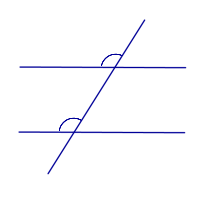	Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

	Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны

Прямые параллельны тогда и только тогда,
когда соответственные углы равны

Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°

Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°

Рисунок	Признак параллельности
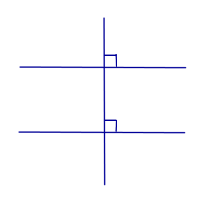	Две прямые, перпендикулярные к третьей прямой, параллельны

Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых

Рисунок	Признак параллельности
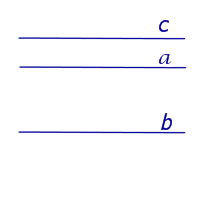	Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c

Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c

Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.

Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.