Как построить окружность под углом черчение (5 видео)

Чертежик

Содержание

Метки
Построение овала
Изображение окружностей в изометрической проекции
Построение изометрических проекций деталей
Понятие о диметрической прямоугольной проекции
Технический рисунок
ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ ОКРУЖНОСТЕЙ
💡 Видео

Метки

Видео:Сопряжение острого углаСкачать

Построение овала

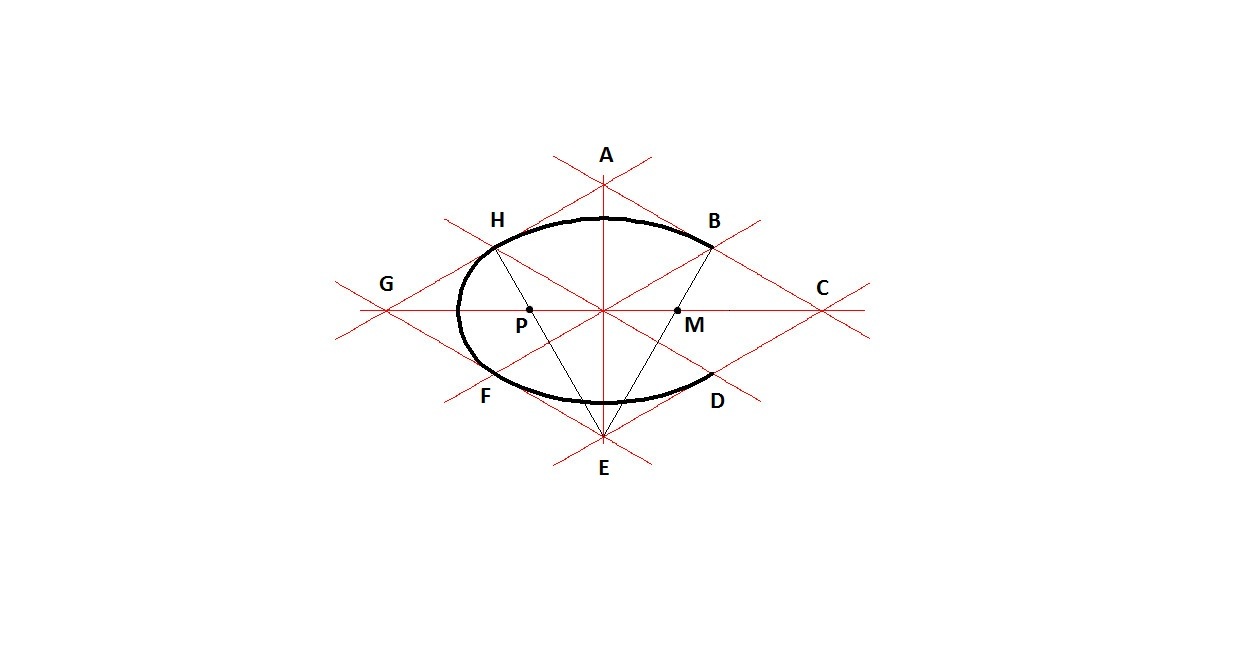
Рассмотрим построение овала двумя методами: окружности и параллелограмма.

Воспользуемся методом окружности.

1.) Начинаем чертить с построения осей.

2.) Чертим окружность

3.) Чертим дуги ЕА и BD радиусом ЕС

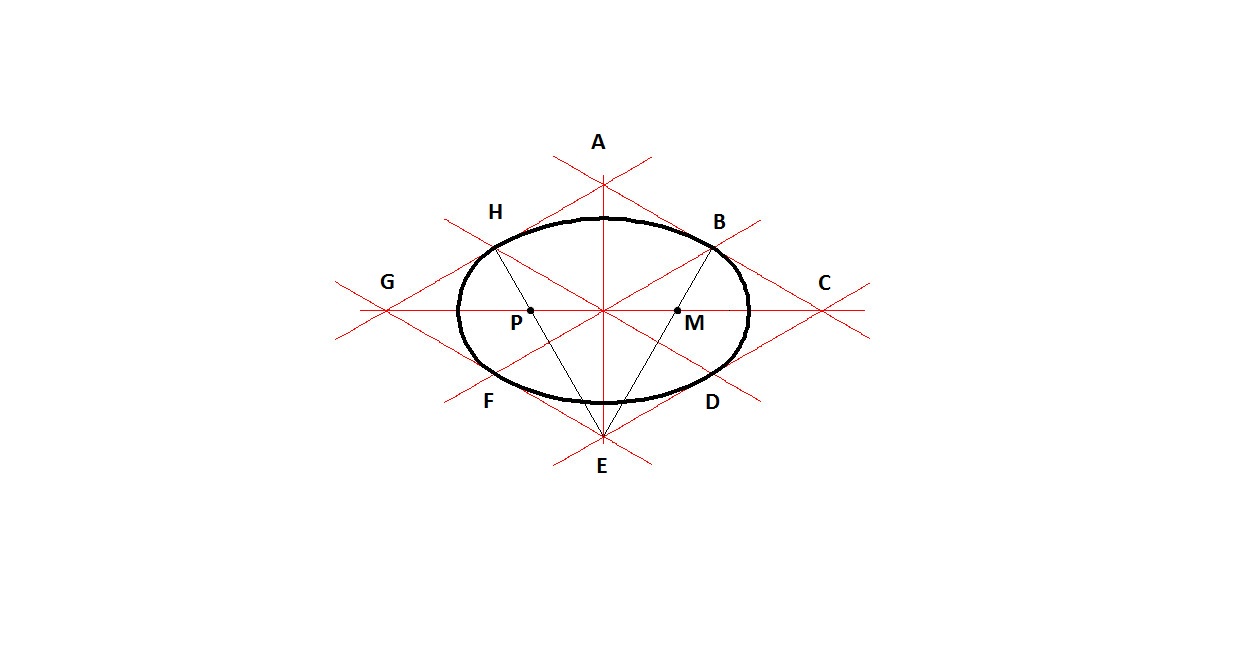
4.) Чертим дуги ED и AB радиусом FB

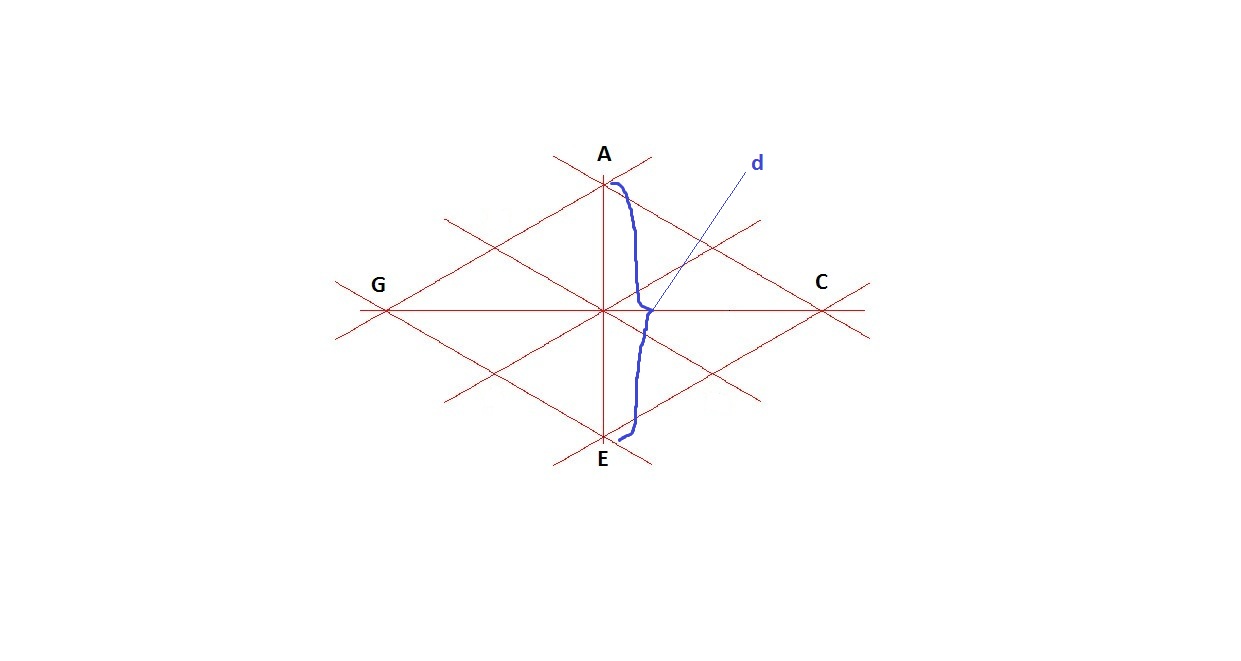
Применим метод параллелограмма.

1.) Начинаем с построения осевых линий

2.) Чертим линии параллельные осевым линиям. Где d — диаметр окружности.

3.) Строим дуги HB и DF радиусом HE4.) Продолжаем с черчения дуги BD радиуса MB и дуги FH радиусом PH

Применение построения овала на чертежах вы можете посмотреть здесь

Видео:1 2 4 сопряжение окружностейСкачать

Изображение окружностей в изометрической проекции

Рассмотрим, как в изометрической проекции изображаются окружности. Для этого изобразим куб с вписанными в его грани окружностями (рис. 3.16). Окружности, расположенные соответственно в плоскостях, перпендикулярных осям х, у, z, изображаются в изометрии в виде трех одинаковых эллипсов.

Рис. 3.16. Изометрические проекции окружностей, вписанных в грани куба

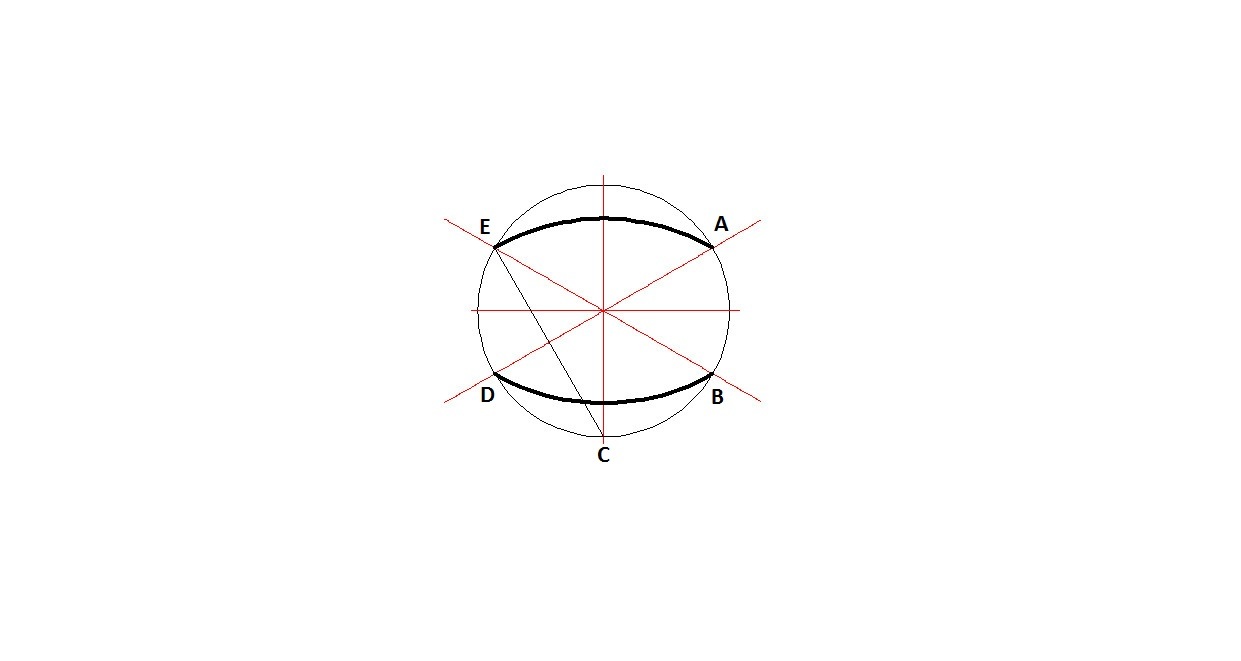
Для упрощения работы эллипсы заменяют овалами, очерчиваемыми дугами окружностей, их строят так (рис. 3.17). Вычерчивают ромб, в который должен вписываться овал, изображающий данную окружность в изометрической проекции. Для этого на осях откладывают от точки О в четырех направлениях отрезки, равные радиусу изображаемой окружности (рис. 3.17, а). Через полученные точки a, b, с, d проводят прямые, образующие ромб. Его стороны равны диаметру изображаемой окружности.

Рис. 3.17. Построение овала

Из вершин тупых углов (точек А и В) описывают между точками а и b, а также с и d дуги радиусом R, равным длине прямых Ва или Вb (рис. 3.17, б).

Точки С и Д лежащие на пересечении диагонали ромба с прямыми Ва и Вb, являются центрами малых дуг, сопрягающих большие.

Малые дуги описывают радиусом R, равным отрезку Са (Db).

Видео:Аксонометрические Проекции Окружности #черчение #окружность #проекции #изометрияСкачать

Построение изометрических проекций деталей

Рассмотрим построение изометрической проекции детали, два вида которой даны на рис. 3.18, а.

Построение выполняют в следующем порядке. Сначала вычерчивают исходную форму детали – угольник. Затем строят овалы, изображающие дугу (рис. 3.18, б) и окружности (рис. 3.18, в).

Рис. 3.18. Последовательность построения изометрической проекции детали

Для этого на вертикально расположенной плоскости находят точку О, через которую проводят изометрические оси х и z. Таким построением получают ромб, в который вписана половина овала (рис. 3.18, б). Овалы на параллельно расположенных плоскостях строят перенесением центров дуг на отрезок, равный расстоянию между данными плоскостями. Двойными кружочками на рис. 3.18 показаны центры этих дуг.

На тех же осях х и z строят ромб со стороной, равной диаметру окружности d. В ромб вписывают овал (рис. 3.18, в).

Находят центр окружности на горизонтально расположенной грани, проводят изометрические оси, строят ромб, в который вписывают овал (рис. 3.18, г).

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Понятие о диметрической прямоугольной проекции

Расположение осей диметрической проекции и способ их построения приведены на рис. 3.19. Ось z проводят вертикально, ось х – под углом около 7° к горизонтали, а ось у образует с горизонталью угол приблизительно в 41° (рис. 3.19, а). Построить оси можно, пользуясь линейкой и циркулем. Для этого из точки О откладывают по горизонтали вправо и влево по восемь равных делений (рис. 3.19, б). Из крайних точек восставляют перпендикуляры. Высота их равна: для перпендикуляра к оси х – одному делению, для перпендикуляра к оси у – семи делениям. Крайние точки перпендикуляров соединяют с точкой О.

Рис. 3.19. Расположение осей диметрической проекции

При вычерчивании диметрической проекции, как и при построении фронтальной, размеры по оси у сокращают в 2 раза, а по осям х и z откладывают без сокращений.

На рис. 3.20 показана диметрическая проекция куба с вписанными в его грани окружностями. Как видно из этого рисунка, окружности в диметрической проекции изображаются эллипсами.

Рис. 3.20. Диметрические проекции окружностей, вписанных в грани куба

Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Технический рисунок

Технический рисунок – это наглядное изображение, выполненное по правилам аксонометрических проекций от руки, на глаз. Им пользуются в тех случаях, когда нужно быстро и наглядно показать на бумаге форму предмета. Обычно в этом возникает необходимость при конструировании, изобретательстве и рационализации, а также при обучении чтению чертежей, когда с помощью технического рисунка нужно пояснить форму детали, представленной на чертеже.

Выполняя технический рисунок, придерживаются правил построения аксонометрических проекций: под теми же углами располагают оси, так же сокращают размеры по осям, соблюдают форму эллипсов и последовательность построения.

Видео:Как начертить овал. Эллипс вписанный в ромбСкачать

ИЗОМЕТРИЧЕСКАЯ ПРОЕКЦИЯ ОКРУЖНОСТЕЙ

Окружности в изометрической проекции изображаются эллипсами (рис. 2.55). Их строят с помощью специальных инструментов — лекал. Это процесс трудоемкий. Поэтому в практике выполнения чертежей эллипсы заменяют овалами. Овал — кривая, состоящая из четырех дут окружности.

Рассмотрим построение овала в горизонтальной плоскости, представляющего собой изометрическую проекцию окружности. Строить овал целесообразно путем вписывания его в ромб, который является изометрической проекцией квадрата, описанного вокруг окружности (рис. 2.56, а).

1. Строим оси хиу изометрической проекции (рис. 2.56, б).
2. Строим аксонометрическое изображение квадрата, описанного вокруг окружности. Обратите внимание, что сторона квадрата равна диаметру окружности. Для этого от точки О на осях х и у откладывают отрезки, равные радиусу изображаемой окружности.
3. Через точки, полученные на оси х — 4 и 2, проводим прямые, параллельные оси у, а через точки на оси у — прямые, параллельные оси х. Получим ромб. Отметим точки А и В и проведем большую диагональ ромба, которая пройдет через точку О (рис. 2.56, в).

4. Из вершин тупых углов ромба точек А и В проводим дуги. Их радиус равен расстоянию от вершин тупого угла до точек 4, 3 или /, 2 соответственно (рис. 2.56, г).

Чтобы найти центры меньших дуг овала, через точки А и 4, А и 3 проводят прямые, которые, пересекаясь с большей диагональю ромба, дадут нам точки, которые будут центрами Oj и 0₂ малых дуг овала. Их радиус равен /. Дугами радиуса /?, проводят малые дуги овала (рис. 2.56, д, е).

Аналогичным способом строят овалы, лежащие во фронтальной и профильной плоскостях. Для овала во фронтальной плоскости построение ведут по осям хи^,ав профильной плоскости — по осям zny (рис. 2.57).

На рис. 2.58 показано построение овала без вписывания его в ромб.