- Процесс построения
- Подготовительный этап
- Порядок действий
- Альтернативный вариант
- Полезные советы
- Как построить из окружности биссектрису угла
- Как можно построить биссектрису угла с помощью циркуля и линейки?
- Процесс построения
- Подготовительный этап
- Порядок действий
- Альтернативный вариант
- Полезные советы
- Биссектриса угла с помощью окружности
- Как построить биссектрису данного угла? Задачи на построение
- Как построить биссектрису данного угла?
- Алгоритм построения
- Доказательство
- Как можно построить биссектрису угла с помощью циркуля и линейки?
- Процесс построения
- Подготовительный этап
- Порядок действий
- Альтернативный вариант
- Полезные советы
- Задачи на построение циркулем и линейкой с примерами решения
- Задача 1 (построение угла, равного данному)
- Задача 2 (построение серединного перпендикуляра к отрезку)
- Задача 3 (построение биссектрисы угла)
- Построение треугольника по трем элементам
- Задача 4 (построение треугольника по двум сторонам и углу между ними)
- Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)
- Задача 6 (построение треугольника по трем сторонам)
- Как построить из окружности биссектрису угла
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
Видео:Построение высоты в треугольникеСкачать

Процесс построения
Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.
Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.
Подготовительный этап
Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.
Необходимые предметы:
Порядок действий
Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.
Быстрый способ:
- На листе бумаги рисуют 2 пересекающиеся линии.
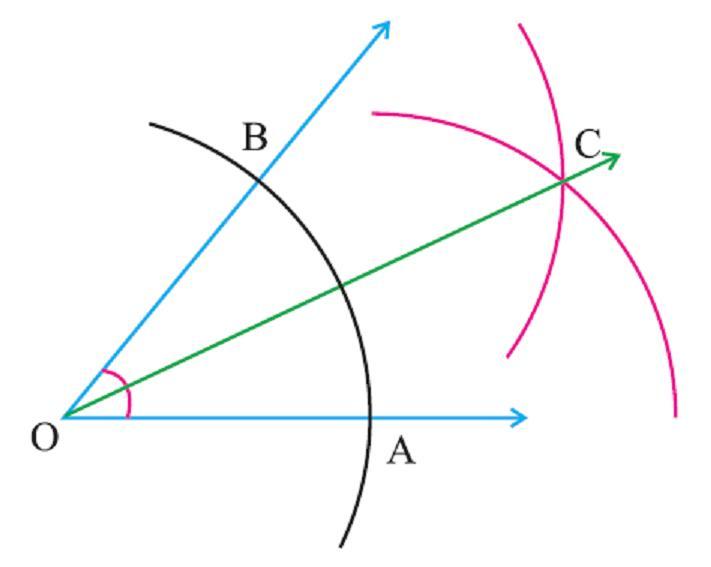
- Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
- Отмечают точками места пересечения сторон угла с окружностью.
- На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
- Находят и отмечают место их пересечения.
- Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
- С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.
С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.
Порядок действий:
- Любым известным способом вписывают окружность в треугольник.
- С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
- Полученные отрезки станут частью искомого луча.
Видео:Построить биссектрису угла. Построение с помощью циркуля и линейки.Скачать

Альтернативный вариант
Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.
Правильная последовательность действий:
- Нулевое значение на шкале прикладывают к вершине.
- Совмещают линейку транспортира с одним из лучей и определяют величину угла.
- Полученное значение делят пополам.
- Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
- Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.
Видео:Построение биссектрисы в треугольникеСкачать

Полезные советы
В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.
Полезные рекомендации:
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
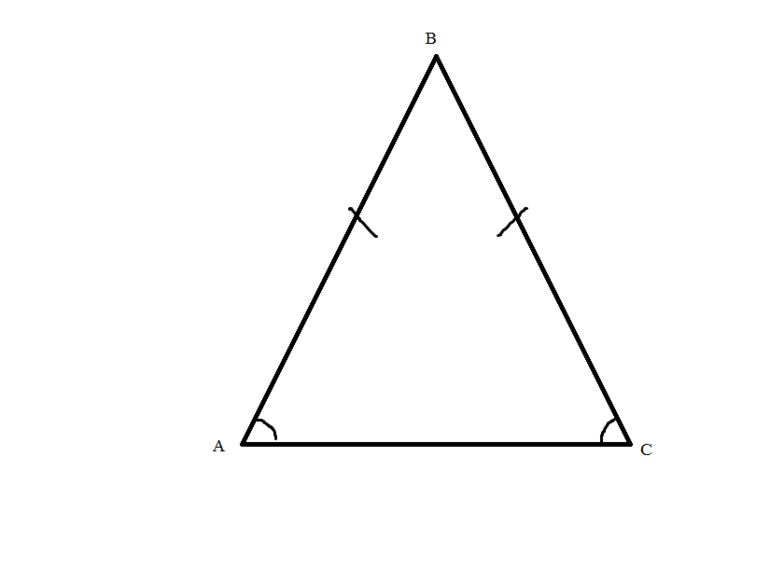
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.
Видео:Построение биссектрисы углаСкачать

Как построить из окружности биссектрису угла
Видео:Построение медианы в треугольникеСкачать

Как можно построить биссектрису угла с помощью циркуля и линейки?
Видео:Биссектриса треугольника. Построение. 1 частьСкачать

Процесс построения
Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.
Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.
Подготовительный этап
Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.
Необходимые предметы:
Порядок действий
Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.
Быстрый способ:
- На листе бумаги рисуют 2 пересекающиеся линии.
- Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
- Отмечают точками места пересечения сторон угла с окружностью.
- На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
- Находят и отмечают место их пересечения.
- Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
- С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.
С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.
Порядок действий:
- Любым известным способом вписывают окружность в треугольник.
- С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
- Полученные отрезки станут частью искомого луча.
Видео:№154. Дан треугольник ABC. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника.Скачать

Альтернативный вариант
Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.
Правильная последовательность действий:
- Нулевое значение на шкале прикладывают к вершине.
- Совмещают линейку транспортира с одним из лучей и определяют величину угла.
- Полученное значение делят пополам.
- Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
- Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.
Видео:Построение биссектрисы угла. 7 класс.Скачать

Полезные советы
В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.
Полезные рекомендации:
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.
Видео:Построение биссектрисы углаСкачать

Биссектриса угла с помощью окружности
Видео:№102. Начертите треугольник. С помощью транспортира и линейки проведите его биссектрисы.Скачать
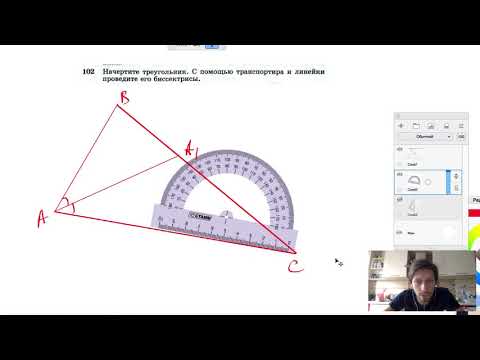
Как построить биссектрису данного угла? Задачи на построение
Существует такой забавный детский стишок, с помощью которого легко запомнить, что такое биссектриса: «Биссектриса — это такая крыса, что бегает по углам и делит угол пополам». Однако нельзя забывать, что, несмотря на простоту запоминания этого шуточного определения, учитель справедливо потребует другое, взятое из учебника.
В дальнейшем изучении школьной программы дети сталкиваются со сложной с первого взгляда задачей — как построить биссектрису данного угла с помощью циркуля. Однако уже более продвинутый школьник без труда справится с этим заданием, которое является основой выполнения цикла задач на построение в геометрии. Давайте же разберемся с этим вопросом раз и навсегда.
Видео:ПОСТРОЕНИЕ ВЫСОТЫ ТРЕУГОЛЬНИКА С ПОМОЩЬЮ ЦИРКУЛЯ. ЗАДАЧИ НА ПОСТРОЕНИЕ | ГЕОМЕТРИЯ 7 классСкачать

Как построить биссектрису данного угла?

Самым очевидным и наиболее простым способом является использование транспортира, но если данного вспомогательного инструмента не оказалось под рукой, надо уметь строить биссектрису без него.
Для выполнения данной задачи, как уже понял читатель, нам потребуется циркуль, а помимо него — линейка (важно понимать, что делениями на ней пользоваться нельзя) и простой карандаш с ластиком.
Видео:Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Алгоритм построения
Необходимо совершить такие действия:
Мы дали ответ на поставленный вопрос — как построить биссектрису данного угла.
Видео:Как построить высоту в треугольнике?Скачать

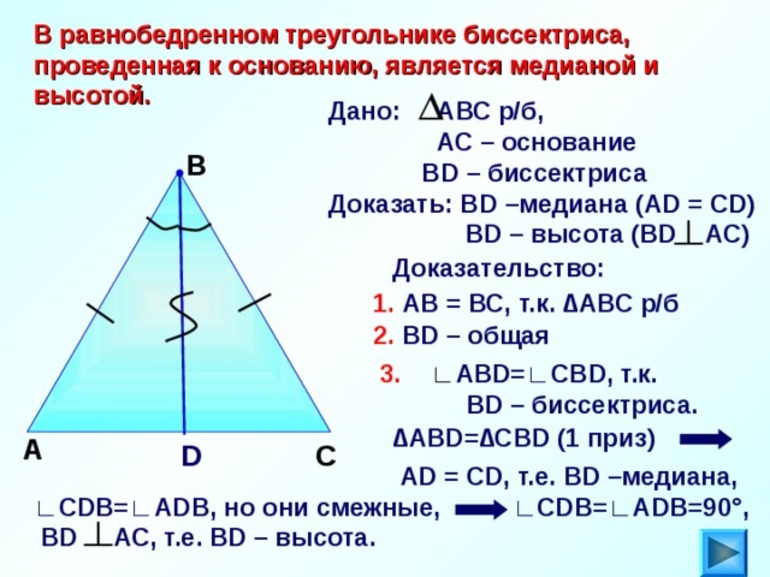
Доказательство
Теперь, разобравшись, как построить биссектрису данного угла, стоит вспомнить еще одно определение биссектрисы, используя термин «геометрическое место точек». Биссектрисой называется геометрическое место точек, которые равноудалены от лучей, образующих угол.
Согласно выполненному построению в пунктах 4-6, точка, принадлежащая построенной биссектрисе, также принадлежит двум окружностям, равным по радиусу, центр которых располагается на лучах, образующих угол на одинаковом расстоянии от вершины угла (согласно пунктам 1-3 построения). Опустим перпендикуляр из отмеченной в пункте 6 точки на лучи, образующие угол. Докажем, что получившиеся прямоугольные треугольники равны, и выясним, что опущенные перпендикуляры также равны, как соответствующие элементы треугольников. Таким образом, их общая гипотенуза является биссектрисой угла по определению. Что и требовалось доказать.
Видео:Задачи на построение с помощью циркуля и линейки - 7 класс геометрияСкачать

Как можно построить биссектрису угла с помощью циркуля и линейки?
Видео:Как построить биссектрису угла с помощью одной линейкиСкачать

Процесс построения
Биссектриса (лат. bisectio) представляет собой геометрическое место точек внутри угла (острый, прямой или тупой), которые одинаково удалены от обеих его сторон.
Для её построения нужно подготовить различные школьные принадлежности и выполнить несколько простых действий.
Подготовительный этап
Чтобы быстро найти биссектрису треугольника с помощью циркуля, нужно провести тщательную подготовку. Она заключается в поиске школьных принадлежностей, которые будут использоваться при построении.
Необходимые предметы:
Порядок действий
Нарисовать луч, разделяющий пополам угол, можно при помощи транспортира. Однако если этой школьной принадлежности нет в наличии, заменить её сможет обыкновенный циркуль.
Быстрый способ:
- На листе бумаги рисуют 2 пересекающиеся линии.
- Чтобы построить биссектрису данного угла, в его вершину ставят ножку циркуля и чертят окружность произвольного радиуса.
- Отмечают точками места пересечения сторон угла с окружностью.
- На них поочерёдно ставят циркуль и, не меняя радиус, рисуют 2 дуги.
- Находят и отмечают место их пересечения.
- Стирают дуги ластиком, чтобы они не мешали дальнейшей работе.
- С помощью линейки и простого карандаша проводят искомый отрезок, соединяющий вершину угла с точкой пересечения дуг.
С помощью циркуля можно легко найти биссектрису треугольника (всякого). Для этого понадобится стандартный набор школьных принадлежностей и наличие базовых знаний геометрии.
Порядок действий:
- Любым известным способом вписывают окружность в треугольник.
- С помощью карандаша и линейки из её центра проводят линии к каждой вершине.
- Полученные отрезки станут частью искомого луча.
Видео:Точка пересечения высот треугольника.Скачать

Альтернативный вариант
Если у ученика нет циркуля, то начертить луч, разделяющий угол пополам, можно и без этой школьной принадлежности. Для работы понадобится линейка, карандаш и транспортир.
Правильная последовательность действий:
- Нулевое значение на шкале прикладывают к вершине.
- Совмещают линейку транспортира с одним из лучей и определяют величину угла.
- Полученное значение делят пополам.
- Затем заново прикладывают транспортир и откладывают величину, полученную в результате расчётов.
- Через эту точку и вершину проводят отрезок, который будет являться искомым лучом.
Видео:Биссектрисы треугольника.Скачать

Полезные советы
В некоторых случаях для нахождения не нужно использовать транспортир и циркуль. Это возможно только тогда, когда нужно определить расположение биссектрисы в треугольнике.
Полезные рекомендации:
- Биссектриса всегда разделяет противолежащую сторону треугольника в отношении, равном пропорции 2 других сторон геометрической фигуры.
- В равнобедренном треугольнике биссектрисы всегда пересекаются под прямым углом.
- Если треугольник равносторонний, то все биссектрисы будут параллельны противоположным сторонам. При этом длина образованных отрезков будет одинаковой.
Построить биссектрису угла с помощью циркуля сможет даже двоечник. Для этого ему понадобится минимум времени, знаний и усилий. Подробно изучив порядок действий, каждый учащийся сможет легко поделить любой угол пополам и объяснить этот процесс одноклассникам.
Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Задачи на построение циркулем и линейкой с примерами решения
Содержание:
Основные задачи на построение циркулем и линейкой:
В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.
При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:
- с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
- с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.
Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.
Видео:7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Задача 1 (построение угла, равного данному)
От данного луча OF отложите угол, равный данному углу ABC.
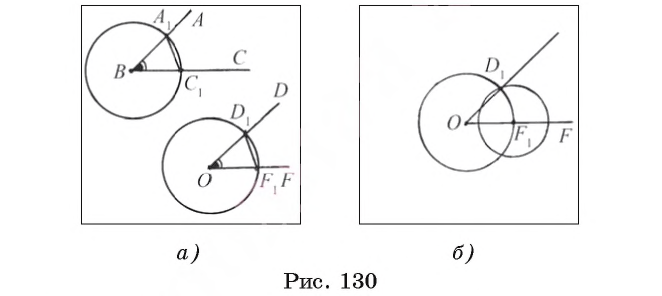
Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).
Пусть
1) Строим окружность 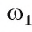
2) Строим окружность 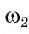
3) Строим окружность 
4) Пусть D1 — одна из точек пересечения окружностей 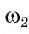



Равенство 



Видео:Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

Задача 2 (построение серединного перпендикуляра к отрезку)
Постройте серединный перпендикуляр к данному отрезку АВ.
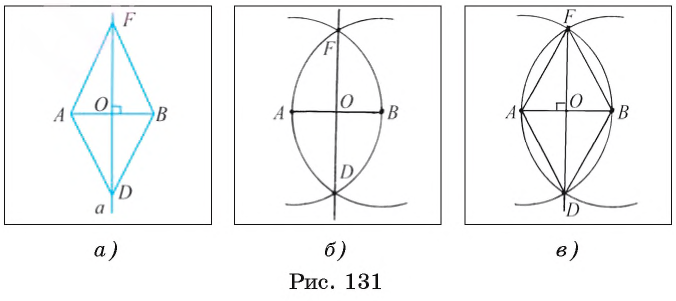
Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности 

1) Строим окружности 




2) Отмечаем точки F и D пересечения окружностей 

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.
Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, 

Задача 3 (построение биссектрисы угла)
Постройте биссектрису данного угла ABC.
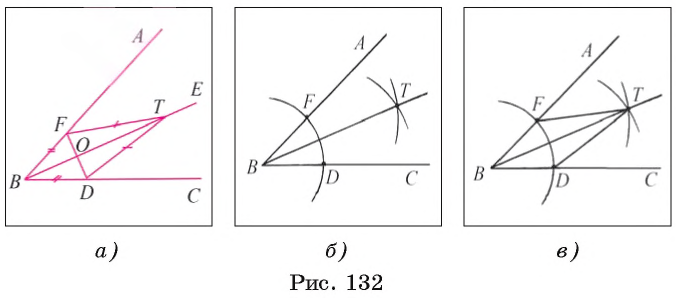
Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD 
1) Строим окружность 
2) Отмечаем точки F и D, в которых окружность 
3) Строим окружности 


4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.
Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что 

Построение треугольника по трем элементам
В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.
Задача 4 (построение треугольника по двум сторонам и углу между ними)
Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.
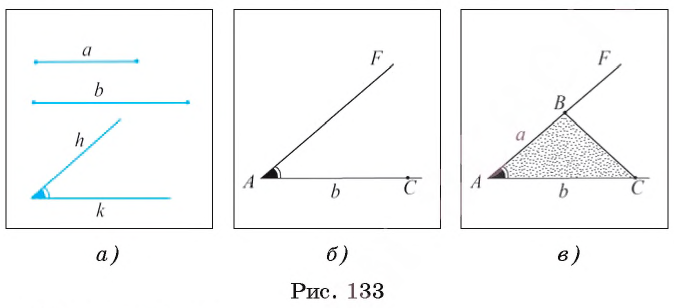
Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.
1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).
2) Строим угол CAF, равный углу hk.
3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).
По построению имеем, что АС = b, АВ = а и 

При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.
Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)
Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.
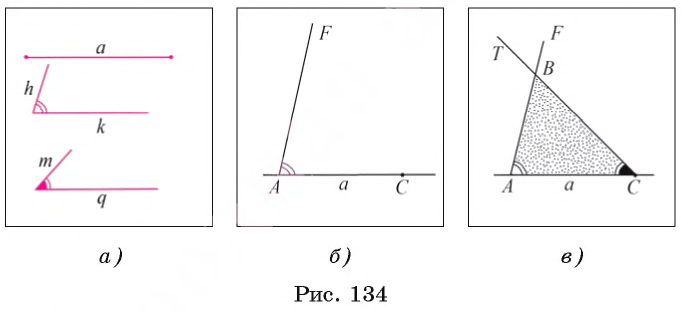
Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.
1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).
2) Строим угол CAF, равный углу hk.
3) Строим угол ACT, равный углу mq.
4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).
По построению имеем, что АС = a, 



Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.
Задача 6 (построение треугольника по трем сторонам)
Постройте треугольник, стороны которого равны данным отрезкам а, b, с.
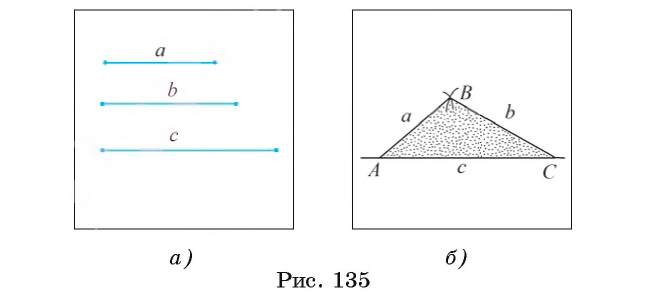
Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.
1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).
2) Строим окружность 
3) Строим окружность 
4) Пусть В — одна из точек пересечения окружностей 

По построению АС = с, АВ = а, ВС = b.
Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Задачи на построение по геометрии
- Угол — определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Соотношения между сторонами и углами треугольника
- Неравенство треугольника — определение и вычисление
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как построить из окружности биссектрису угла
Обновите свой браузер, чтобы видеть это содержимое!
Построение биссектрисы угла
(для демонстрации последовательно нажимайте кнопки с номерами)
(Примечание. Окружности 2 и 3 построены не полностью, чтобы не «загромождать» рисунок.)
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d6f31efeb997b63 • Your IP : 85.95.188.35 • Performance & security by Cloudflare