Внутри треугольника две касающиеся окружности

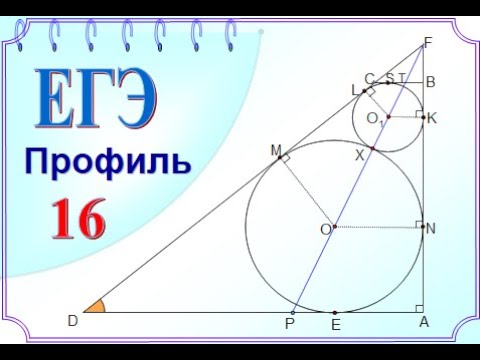
Дан треугольник со сторонами 26, 26 и 20. Внутри него расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.

Рассмотрим равнобедренный треугольник ABC, в котором AB = AC = 26, BC = 20. Пусть AH — высота треугольника ABC. Тогда H — середина BC.

Обозначим ∠ABC = ∠ACB = α. Тогда

Предположим, что окружность радиуса r с центром O₁ вписана в угол ACB и касается основания BC в точке N, а окружность того же радиуса с центром O₂ вписана в угол ABC, касается основания BC в точке M, а первой окружности — в точке D. Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому

а

Из прямоугольного треугольника BMO₂ находим:

Тогда Линия центров касающихся окружностей проходит через точку их касания, поэтому O₁O₂ = 2r, значит, MN = O₁O₂ = 2r, поскольку O₁O₂MN — прямоугольник. Следовательно,

откуда находим r = 4.

Пусть теперь окружность радиуса r с центром O₁ вписана в угол BAC и касается боковой стороны AB в точке P, вторая окружность радиуса r с центром O₂ вписана в угол ABC, касается боковой стороны AB в точке Q, а также касается первой окружности.

Из прямоугольных треугольников APO₁ и BQO₂ находим:

Следовательно,

откуда находим

В случае, когда окружности вписаны в углы BAC и ACB, получим тот же результат.

Ответ: 4 или

Видео:ЕГЭ Задание 16 Две касающиеся окружностиСкачать

Внутри правильного треугольника со стороной 1 помещены две касающиеся друг друга окружности, каждая из которых касается двух сторон треугольника (каждая сторона треугольника касается хотя бы одной окр?

Геометрия | 5 — 9 классы

Внутри правильного треугольника со стороной 1 помещены две касающиеся друг друга окружности, каждая из которых касается двух сторон треугольника (каждая сторона треугольника касается хотя бы одной окружности).

Доказать, что сумма радиусов этих окружностей не меньше, чем (√3 — 1) / 2.

АВС проведем высоту ВК к основанию АС.

ВК — высота, биссектриса и медиана, делит треуг.

АВС на 2 равных прямоугольных треугольника АВК и КВС

АВК АВ = 1 — гипотенуза

АК = 1 : 2 = 0, 5 — катет

ВК2 = АВ2 — АК2 — катет

ВК = корень из 1 * 1 — 0, 5 * 0, 5 = 0, 87

Радиус вписанной в прямоугольный треугольник окружности

r = (р — а)(р — b)(p — c) / p

r = (0, 5 + 0, 87 — 1) / 2

2r = 0, 185 * 2 = 0, 37

(корень из 3 — 1) / 2 = 0, 37

Ответ : сумма радиусов не меньше, чем 0, 37.

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Основание AC равнобедренного треугольника ABC равно 12?

Основание AC равнобедренного треугольника ABC равно 12.

Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC .

Найдите радиус окружности, вписанной в треугольник ABC.

Видео:Задача. Две окружности касаются внутренним образом.Скачать

Дан прямоугольный треугольник ABC с гипотенузой AB?

Дан прямоугольный треугольник ABC с гипотенузой AB.

Окружность радиуса 24 касается стороны BC и продолжений двух других сторон.

Окружность радиуса 18 касается стороны AC и продолжений двух других сторон.

Найти длину стороны AB.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

В треугольнике ABC вписанная окружность касается стороны AB в точке K?

В треугольнике ABC вписанная окружность касается стороны AB в точке K.

Другая окружность касается продолжений сторон АС, ВС и касается стороны АВ в точке L.

Докажите, что AL = BK.

Видео:ЕГЭ планиметрия. Две касающиеся окружностиСкачать

Стороны треугольника равны 39 см, 65 см и 80 см?

Стороны треугольника равны 39 см, 65 см и 80 см.

Окружность, центр которой принадлежит больше стороне треугольника, касается двух других сторон.

На какие отрезки центр этой окружности делит сторону треугольника ?

Видео:Так периметр еще никто не находил! Задача про треугольник и окружностиСкачать

В равнобедренном треугольнике боковая сторона равна 10, а основание равно 12?

В равнобедренном треугольнике боковая сторона равна 10, а основание равно 12.

Окружность с центром на стороне треугольника касается двух других его сторон.

Найдите радиус окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

. Внутри окружности радиуса R расположены три окружности радиуса r , касающиеся друг друга внешним образом, каждая из которых касается большей окружности внутренним образом?

. Внутри окружности радиуса R расположены три окружности радиуса r , касающиеся друг друга внешним образом, каждая из которых касается большей окружности внутренним образом.

Определите разность площади большей окружности и суммы площадей меньших окружностей.

Видео:Пара касающихся окружностей | Осторожно, спойлер! | Борис Трушин |Скачать

Дан равнобедренный треугольник АВС с основанием AC = 4?

Дан равнобедренный треугольник АВС с основанием AC = 4.

Радиус окружности, которая касается основания АC и касается продолжения сторон ВА и ВС, равен 4.

Найти радиус окружности, вписанной в треугольник АВС, и боковую сторону.

Видео:ЕГЭ Задание 16 Комбинация трёх окружностейСкачать

СРОЧНО НАДО?

ЕГЭ! ПОМОГИТЕ ПОЖАЛУЙСТА!

Дан треугольник со сторонами 115, 115 и 184.

Внутри его расположены 2 равные касающие окружности, каждая из которых касается двух сторон треугольника.

Найдите радиусы окружностей.

Видео:ТОП-3 конструкции с окружностями для №16 из ЕГЭ 2023 по математикеСкачать

Окружность радиуса R касается сторон угла , градусная мера которого равна 60 * ?

Окружность радиуса R касается сторон угла , градусная мера которого равна 60 * .

Найдите радиус меньшей окружности , которая касается сторон угла и данной окружности.

Видео:КАСАЮЩИЕСЯ ОКРУЖНОСТИСкачать

Две касающиеся внешним образом в точке К окружности, радиусы которых равны 40 и 42, касаются сторон угла с вершиной А?

Две касающиеся внешним образом в точке К окружности, радиусы которых равны 40 и 42, касаются сторон угла с вершиной А.

Общая касательная к этим окружностям, проходящая через точку К, пересекает стороны угла в точках В и С.

Найдите радиус окружности, описанной около треугольника АВС.

Если вам необходимо получить ответ на вопрос Внутри правильного треугольника со стороной 1 помещены две касающиеся друг друга окружности, каждая из которых касается двух сторон треугольника (каждая сторона треугольника касается хотя бы одной окр?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Материалы для подготовки к ЕГЭ. Задача С4.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:ПЛАНИМЕТРИЯ ЕГЭ | 16 задача из 1 варианта Ященко 2021 🔴Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Материалы для подготовки к ЕГЭ. Задача С4

Задание С4. Решение многовариантных задач по планиметрии.

Наиболее часто используемые теоретические сведения : признаки подобия треугольников; теорема Пифагора; теорема косинусов; теорема синусов; свойства средней линии треугольника и средней линии трапеции; формулы радиусов вписанной и описанной окружностей; формула длины отрезка стороны треугольника до точки касания со вписанной окружностью; свойство медианы треугольника; свойство биссектрисы угла треугольника; формулы площади треугольника, параллелограмма, трапеции, произвольного четырехугольника (через диагонали и угол между ними); свойства углов, связанных с окружностью (центральный, вписанный, угол между касательной и секущей, угол между секущими, угол между хордами); свойство пропорциональности отрезков хорд, свойство пропорциональности отрезков секущих, теорема о касательной и секущей; соотношения, связанные с высотой в прямоугольном треугольнике; свойства и признаки четырехугольника, вписанного в окружность, и описанного около окружности; условия нахождения четырех точек на одной окружности (на одной дуге или на дополнительных дугах); отрезок, соединяющий основания двух высот треугольника, отсекает подобный исходному треугольник.

Полезные навыки при решении задач : дополнительные построения в трапеции (проведение через вершину прямой, параллельной боковой стороне; проведение высот; пересечение продолжений боковых сторон; проведение прямой до пересечения с продолжением основания через вершину и точку на боковой стороне); навыки вычисления отношений пересекающихся отрезков, умение вычислять отношения площадей фигур, знание привычных вариантов расположения подобных треугольников, привычный поиск прямоугольного треугольника, связанного с касающимися окружностями.

Необходимо знать : точка касания двух окружностей лежит на прямой, соединяющей их центры; отношение высот треугольника обратно пропорционально отношению сторон; в произвольной трапеции точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой; отношение площадей треугольников с общим углом или со смежными углами равно произведению отношений сторон, прилежащих к указанному углу;

Основные причины возникновения нескольких случаев в выполнении чертежа, проведении решения или написании ответа:

Не указано, где именно расположена точка на прямой: на стороне фигуры или на ее продолжении;

Не указано, считать отношение, данное в условии, от одного конца отрезка, или же от другого;

Не указано, происходит внешнее касание окружностей, или же внутреннее;

Не указано, пересекаются прямые(лучи) внутри фигуры, или же вне ее;

Не указано, в какую именно из областей вписана окружность;

Не указано, как именно расположена прямая, образующая с данной прямой данный угол;

Не указано, лежит ли основание высоты треугольника на его стороне или на ее продолжении (острый угол или тупой);

Возможны два треугольника с заданным синусом угла (угол тупой или острый);

Не указано, расположены центры двух пересекающихся окружностей — по одну сторону от общей хорды, или же по разные;

Не указано, проведена внешняя или внутренняя общая касательная.

Сложности могут возникнуть:

При обнаружении всех случаев расположения фигур или всех возможных конфигураций фигуры. (внимательно читаем и запоминаем предыдущий раздел)

При составлении уравнений. (советуем вспомнить все факты, касающиеся данной ситуации, и проверить, не дают ли они нужное недостающее уравнение)

При изменении уравнения в соответствии с новой конфигурацией. (советуем запомнить, какие точки участвовали в предыдущем случае, и называть соответствующие точки точно так же. Скорее всего, уравнение получится таким же или почти таким же.

При решении полученных уравнений. Если все совсем плохо, подумайте, а не слишком ли тяжелый способ решения Вы избрали. Возможно, на поверхности лежит другой, намного легче…

Конечно, нужно как можно больше тренировать внимательность и аккуратность. Одна ошибка в арифметике на любом этапе решения задачи может зачеркнуть все сделанное!

1) если какое-либо условие дано, то, вероятно, оно должно быть использовано при решении; если Вы не можете решить задачу, проверьте, все ли данные осознаны и использованы.

2) Если в задаче речь идет о касающихся окружностях, то сразу, автоматически, рассматриваем внешнее и внутреннее касание, и в каждом случае проводим прямую центров, на которой обязательно лежит точка касания. (хорошо выражаются отрезки, равные сумме или разности радиусов)

3) Если в задаче окружность касается прямой, то сразу проводим радиус в точку касания, он будет перпендикулярен касательной.

4) Если две окружности имеют общую касательную, то, во-первых, если ничего не указано, то их две (существенно различных): внешняя и внутренняя, а, во-вторых, расстояние между точками касания с прямой легко вычисляется с помощью построения «волшебного» прямоугольного треугольника.

5) Если в задаче найдено два варианта расположения, посмотрите, нет ли еще!

6) Если Вы просчитали все случаи и получили несколько ответов, посмотрите, все ли они подходят по условию….

Задание может содержать два и более случаев. Если Вы рассмотрите все случаи и не успеете (не сумеете?) довести ни один до правильного ответа, то есть шанс получить хотя бы балл.

Один случай, полностью решенный, доведенный до правильного ответа, дает более половины баллов за задачу!

Не боги горшки обжигают. Если Вы знаете много стандартных конфигураций, и знаете, как с ними справляться, не понаслышке, а прорешав множество задач, то велика вероятность, что и эту незнакомую задачу Вы решить сможете. Смелее!

Если не знаете, что делать, чтобы решить задачу, вываливайте на лист все, что знаете о данной ситуации. Решение может найтись само!

По микроскопическим чертежам решать задачи умеют немногие. Чертеж должен быть хорошим! Он должен Вам помогать, а не мешать. Речь не идет об идеально ровных окружностях. Вы должны видеть на чертеже все необходимое, и линии не должны случайно сливаться, а точки – случайно совпадать!

Характеристика блоков заданий:

Блок 1 – Подготовка к выполнению задач уровня С4. Основные приемы в заданиях весьма умеренного уровня сложности.

Блок 2 – Работа на занятии. Задания немного более высокого уровня, или более комплексные, включающие различные приемы. Заданий достаточно много, преподаватель имеет возможность выбрать, какие примеры надо в первую очередь разобрать на семинарах. Всем, даже хорошо решающим, есть, чем заняться.

Блок 3 – Домашнее задание. Он больше остальных, так как на занятии очень много успеть невозможно, а без тренировки выполнить хорошо задание на экзамене трудно.

Внимание! Задания не всегда расположены в порядке возрастания сложности!

Блок 1. (обязательный минимум-подготовка к задачам ЕГЭ — начало работы на занятии)

1. Дан параллелограмм ABCD . Биссектрисы углов А и D делят сторону ВС на три равные части. Вычислите стороны параллелограмма, если его периметр равен 40.

Два случая возникают из-за того, что лучи могут пересечься как внутри фигуры, так и вне ее. Остается только заметить равнобедренные треугольники.

5, 15, 5, 15 или 8, 12, 8, 12

2. В прямоугольнике , . Точка на прямой выбрана так, что . Найдите .

Опять равнобедренные треугольники! Только надо рассмотреть три возможных расположения точки Е на прямой АВ (на отрезке или вне его). Оказывается, что один из случаев не реализуется. Но это надо доказать…

3. В треугольнике на стороне выбрана точка так, что она делит сторону ВС в отношении 1:2. Медиана пересекает отрезок в точке . Какую часть площади треугольника составляет площадь треугольника ?

Тренируемся находить отношение отрезков либо с помощью дополнительных построений и подобия треугольников, либо по теореме Менелая. Далее ищем «часть от части» площади. Стандартная задача для знающих несложные методы.

или

4. Дан параллелограмм , , , . Окружность с центром в точке касается биссектрисы угла и двух сторон параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь четырехугольника .

Два случая – обе окружности вписаны в правильные треугольники, только один из них «вылезает» за пределы параллелограмма. Далее в одном из вариантов расположения площадь легко собирается «по частям» из треугольников, если заметить, что в них найденный радиус является высотой. Второй случай удобно сводится к первому вычитанием из параллелограмма.

или

5. Найдите длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей равны 23 и 7, а расстояние между центрами окружностей равно 34.

Стандартный алгоритм: радиусы в точку касания, перпендикулярные прямой, точка касания лежит на прямой центров, ищем «волшебный» прямоугольный треугольник с помощью проведения линии, параллельной касательной. Можно прямо запомнить формулу для расстояния между точками касания двух касающихся окружностей с общей касательной. Не забудьте, что касательная может быть как внешняя, так и внутренняя!

6. Около треугольника АВС описана окружность с центром О, угол АОС равен . В треугольник АВС вписана окружность с центром М. Найдите угол АМС.

Надо знать: связь центрального и вписанного углов; Сумму противоположных углов вписанного четырехугольника (для второго варианта расположения); уметь вычислить угол между биссектрисами двух углов треугольника, на пересечении которых лежит упомянутый центр вписанной окружности! Больше ничего… Только аккуратность. И смелость.

или

7. В треугольнике сторона равна 6, высота равна , а сторона равна . Найдите площадь треугольника .

Высота может опуститься как на сторону треугольника, так и на ее продолжение…. Так что надо рассмотреть и случай тупоугольного треугольника тоже!

или

8. На стороне параллелограмма выбрана точка , делящая эту сторону в отношении 2:3. Отрезок пересекает диагональ в точке . Какую часть площади параллелограмма составляет площадь треугольника ?

Простейшие действия с площадями. Знание базовых формул. Желающие могут сделать задачу красиво, без вычислений, только с отношениями, «часть от части». Не забудьте, что не указано, откуда считать отношение!

или

9. Две окружности пересекаются в точках и . Через точку проведены диаметры и этих окружностей. Найдите расстояние между центрами окружностей, если , .

Угол, опирающийся на диаметр, и средняя линия треугольника!

Откуда случаи? Просто центры двух окружностей могут находиться по одну сторону от общей хорды. А могут – по разные.

10. Трапеция с основаниями и вписана в окружность с центром . Найдите высоту трапеции, если ее средняя линия равна 3 и .

Опять центральный угол и вписанный. Желательно знать формулы универсальной тригонометрической подстановки – тогда можно решить задачу чисто алгебраически, даже не понимая, почему два случая…. И когда центр окружности внутри трапеции, а когда – вне!

11. Прямая отсекает от сторон прямого угла отрезки 5 и 12. Найдите радиус окружности, касающейся этой прямой и сторон угла.

Простейший случай вписанной и вневписанной окружности. Радиус вписанной, как положено в прямоугольном треугольнике, даже может быть вычислен как отрезок стороны до точки касания. Формулу для радиуса вневписанной желательно знать, может пригодиться. Чтобы каждый раз не выводить через площади частей!

Блок 2. (задания для работы на занятии)

12. На стороне квадрата построен равносторонний треугольник . Найдите высоту треугольника , проведенную из вершины , если известно, что сторона квадрата равна 1.

Треугольник можно построить как вовнутрь квадрата, так и наружу. Других трудностей в задаче не предполагается! Только немного посчитать.

13. В окружность радиуса вписана трапеция основаниями 2 и 4. Найдите расстояние от центра окружности до точки пересечения диагоналей трапеции.

Трапеция равнобокая; середины оснований и точка пересечения диагоналей лежат не просто на одной прямой, а на оси симметрии! Только надо помнить, что в подобных фигурах высоты, как и любые другие линейные размеры, относятся с тем же коэффициентом, что и стороны!

14. Расстояние между центрами окружностей радиусов 2 и 8 равно 15. Этих окружностей и их общей касательной касается третья окружность. Найдите ее радиус.

Задача-сюрприз. Здесь не два случая, и даже не три…. Можно устраивать конкурс, кто найдет больше! Целых шесть. Два, если общая касательная внутренняя, и четыре, если внешняя!

Справились – приступаем к стандартному вычислению расстояния между точками касания и поиску прямоугольных треугольников.

, или , или , или , или

15. Окружность радиуса 12 вписана в прямоугольную трапецию с основаниями 28 и 21. Найдите радиус окружности, которая касается основания, большей боковой стороны и окружности .

Две окружности закатились в разные уголки…. А по сути – только синус с косинусом меняются местами! Можно даже решать не два случая, а….. скажем, полтора, сославшись на прямой угол между биссектрисами углов при боковой стороне трапеции. Только посчитать бы нужную функцию угла! Впрочем, поможет очевидное подобие треугольников.

3 или

16. Дана трапеция _{, основания которой Окружность, касающаяся прямых и , касается стороны в точке . Найдите длину отрезка .}

Вот и опять вписанная и вневписанная окружности! Точнее, длины отрезков до точки касания. Правда, предварительно придется поработать с теоремой Пифагора.

17. Прямая, проведенная через середину стороны квадрата , пересекает прямые и в точках и соответственно и образует с прямой угол, тангенс которого равен 4. Найдите площадь треугольника , если сторона квадрата равна 8.

Угол наклона известен, но неизвестно, в какую сторону он отложен! (Возникает ассоциация с декартовой системой координат: модуль коэффициента дан, а знак – нет.) Отсюда два случая. Если не мудрствовать, то далее ничего сложнее формулы площади треугольника через сторону и высоту применять не придется!

18. Площадь трапеции _{равна 90, а одно из оснований трапеции вдвое больше другого. Диагонали пересекаются в точке О; отрезки, соединяющие середину Р основания с вершинами В и С, пересекаются с диагоналями трапеции в точках М и N соответственно. Найдите площадь четырехугольника OMPN .}

Раздолье для любителей вычислять отношения площадей. Можно коллекционировать способы. Сложение-вычитание, «часть от части». Вопрос – что увидишь на чертеже! Не забыть, что не сказано, середина какого именно основания дана – большего или меньшего. Варианты…

19. Расстояние между параллельными прямыми равно 4. На одной из них лежит точка С, а на другой – точки А и В, причем треугольник АВС – остроугольный равнобедренный, и его боковая сторона равна 5. Найдите радиус окружности, вписанной в треугольник АВС.

Колдуем с теоремой Пифагора… И формула радиуса вписанной окружности. Более ничего. Кроме, разве что, немного забавного расположения треугольника. И спасибо, что он остроугольный по условию!

или

20. Центр окружности радиуса 4 принадлежит биссектрисе угла величиной . Найдите радиус окружности, вписанной в данный угол и касающейся данной окружности, если известно, что расстояние от точки до вершины угла равно 10.

Стоило чуть-чуть оторвать исходную окружность от сторон угла – и какой эффект! Сразу не два случая, а четыре! Вычисления проводим с помощью тех же «волшебных» прямоугольных треугольников. Только уже не пишем на автомате, надо ведь понять, где 5, а где 4, где сложить, а где что вычесть!

2, или 14, или 6, или

21. Дан квадрат со стороной 17 и окружность с центром в точке радиуса 8. Найдите радиус окружности, касающейся окружности , содержащейся внутри квадрата и касающейся двух его соседних сторон.

Три варианта, из которых один совсем тривиальный…. Помним, что точка касания – на прямой центров, и ищем прямоугольные треугольники! Так как углы фигуры – прямые, то все нужные стороны считаются легко.

5, или , или

22. В окружности, радиус которой равен 10, проведена хорда . Точка лежит на хорде так, что . Найдите радиус окружности, касающейся данной окружности и касающейся хорды с точке .

Центры двух окружностей либо по одну сторону от хорды, либо по разные. Прежде, чем считать хорошие прямоугольные треугольники, надо найти расстояние от центра большой окружности до хорды. Конечно, тоже по теореме Пифагора.

или

23. Сторона равностороннего треугольника равна 10. Точка лежит на прямой так, что . Окружности, вписанные в каждый из треугольников и , касаются прямой в точках и соответственно. Найдите длину отрезка .

Длины отрезков сторон до точки касания! Кто знает формулу, для того задачка очень легкая. Если не знать…. Можно долго провозиться с обходными маневрами. Углы считать, например… Да, не забудьте коварные слова «точка лежит на прямой»! Это значит, что придется рассматривать и случай, когда она на продолжении стороны. Спасибо, что в другую сторону не получится из-за данного отношения!

24. Четырехугольник описан около окружности и вписан в другую окружность. Прямые и пересекаются в точке . Найдите периметр треугольника , если известно, что и .

Пропорциональность отрезков секущих и хитрое подобие «перевернутых» треугольников. Тогда все считается, Конечно, мы учли свойства вписанных и описанных четырехугольников. И еще… Мы не знаем, что больше — или . Поэтому такая задача смогла попасть в ЕГЭ.

или

25. Высота равнобедренного треугольника, опущенная на основание, равна 32, а радиус вписанной в треугольник окружности равен 15. Найти радиус окружности, касающейся стороны треугольника и продолжений двух других его сторон.

Опять вневписанные окружности. Правда, треугольник очень уж хороший. Так что задача легко поддастся тем, кто просто видит подобные прямоугольные треугольники и умеет считать углы.

26. На стороне угла , равного , взята такая точка , что и . Найдите радиус окружности, проходящей через точки _{, и касающиеся прямой} .

Очень симпатичная задачка. Применить надо много чего, а считать – легко. Так как окружность может касаться ПРЯМОЙ ВС, получаем два случая. Прямая до вершины угла, или же после. Полезно помнить теорему о касательной и секущей, а также теорему косинусов. И общее правило: Если нужна окружность, проходящая через…. (какие-то точки), то ищите вписанный треугольник! Поможет теорема синусов.

27. В треугольнике на стороне взята точка такая, что . Известно, что . Какую длину может иметь сторона , если известно, что окружность, проходящая через точки и и касающаяся прямой , касается также прямой ?

Теорема о касательной и секущей. Которые (касательные и секущие) надо обязательно видеть! И теорема косинусов. Только здесь может оказаться немного сложно найти второй случай. Как-то не видится, что точка касания с прямой АС может быть за точкой А….

24 или

28. Дан отрезок длины 20. Три окружности радиуса 4 имеют центры в концах этого отрезка и в его середине. Найдите радиус четвертой окружности, касающейся трех данных.

Первое впечатление, возможно, приводит в состояние растерянности…. Три окружности какие-то совсем уж одинаковые, и расположены симметрично…. Но, если подумать, то все ясно: либо две соседние окружности внутри большой, либо одна – средняя. А далее опять все по шаблону – касание на оси центров, перпендикуляры на данный отрезок, прямоугольные треугольники, теорема Пифагора…

или

29. Окружности радиусов 2 и 4 касаются в точке . Через точку проведена прямая, пересекающая второй раз меньшую окружность в точке , а большую окружность – в точке . Известно, что . Найдите .

Как, один ответ? Задача попала в ЕГЭ случайно? Что ж, можно сказать, и так. Только попала из старых вариантов мех-мата МГУ. Так что она – для внимательных!

Итак, если человек делает один чертеж, видит равнобедренные подобные треугольники, радуется, получает правильный ответ….. то – не рассчитывайте на полный балл. Почему? Забыл случай внутреннего касания! Вы не забыли? Что же, молодцы. В ответе еще одно число? Опять полного балла не будет. Потому что здесь надо не только рассмотреть оба типа касания, но и увидеть, что в случае внутреннего касания хорда не влезает в окружность! То есть тут ответа нет. Теперь, когда мы рассмотрели оба случая, а затем отсеяли ненужный, имеем правильное решение!

30. Дана окружность радиуса 2 с центром . Хорда пересекает радиус в точке , причем . Найдите радиус окружности, вписанной в угол и касающейся дуги , если .

Ищем второй вариант расположения. Вы нашли? Увидели внешнее касание? Окружность вписана в угол, а не в часть круга! Теперь можно решать задачу. Надо увидеть, что угол дали замечательный! Он прекрасно делится пополам…. И можно поискать «хороший» треугольник для теоремы Пифагора или для теоремы косинусов – кто что найдет! И еще не испугаться ответов…

или

31. Окружности и радиусов и () соответственно касаются в точке . Через точку , лежащую на окружности , проведена прямая, касающаяся окружности в точке . Найдите , если известно, что .

Задача напоминает №29. Те же подобные равнобедренные треугольники с радиусами… Те же два случая. Только отбрасывать нечего. И посчитать в общем виде. Аккуратно. До ответа (ов).

32. Окружности с центрами и радиуса пересекаются в точке . Радиус окружности с центром перпендикулярен , причем точки и лежат по одну сторону от прямой . Окружность касается меньших дуг и этих окружностей, а также прямой , а окружность касается окружности с центром , прямой и окружности . Найдите отношение радиуса окружности к радиусу окружности .

В задаче можно заблудиться! А всего-то надо увидеть три точки касания с одной и той же прямой! И два случая взаимного расположения окружностей ( и точек касания, соответственно!). Да, еще один прямоугольный треугольничек для связи первого радиуса с исходными. Успехов!

33. Точки — основания высот треугольника АВС. Углы треугольника равны и . Найдите углы треугольника АВС.

Один из углов между двумя высотами треугольника всегда равен углу треугольника.

Если треугольник остроугольный, то прямая, соединяющая основания двух высот треугольника, отсекает от него треугольник, подобный исходному. С коэффициентом, равным косинусу общего угла.

Кстати, если соединить основания всех высот, то получится треугольник, называемый «ортотреугольником». А его биссектрисы лежат на высотах исходного треугольника….

И, если с остроугольным треугольников все ясно, то тупоугольные дают целый букет ответов…. Который можно вычислить только для одного варианта из трех, а остальные к нему свести!

, или , или , или

34. Высоты треугольника АВС пересекаются в точке Н. Известно, что отрезок СН равен радиусу окружности, описанной около треугольника. Найдите угол АСВ.

Ищем угол треугольника между его высотами! Плюс знание теоремы синусов ( с радиусом). И…. возникает замечательный прямоугольный треугольник, где катет вдвое меньше гипотенузы!

или

35. Дана трапеция АВС D с боковыми сторонами , и верхним основанием . Известно, что . Найдите BD .

Можем считать, что нам дали косинус угла при другом основании… (отличается знаком). Далее – работа для теоремы косинусов. Сплошная алгебра… Можно, конечно, придумать и геометрическое решение, но так намного проще.

36 или

,

41. Расстояния от общей хорды двух пересекающихся окружностей до их центров относятся как 2:5. Общая хорда имеет длину , а радиус одной из окружностей в два раза больше радиуса другой окружности. Найдите расстояние между центрами окружностей.

42. Две окружности, радиусы которых равны 9 и 4, касаются внешним образом. Найдите радиус третьей окружности, которая касается двух данных окружностей и их общей внешней касательной.

36 или

43. На стороне квадрата построен равнобедренный прямоугольный треугольник с гипотенузой . Найдите высоту треугольника , проведенную из вершины , если известно, что сторона квадрата равна 1.

или

44. Расстояние между центрами окружностей радиусов 1 и 9 равно 17. Третья окружность касается обеих окружностей и их общей касательной. Найдите радиус третьей окружности.

, или , или , или , или , или

45. Окружность радиуса 24 вписана в равнобедренную трапецию с основаниями 36 и 64. Найдите радиус окружности, которая касается основания, боковой стороны и окружности .

6 или

46. Прямая, проведенная через середину стороны квадрата , пересекает прямые и в точках и соответственно и образует с прямой угол, тангенс которого равен 3. Найдите площадь треугольника , если сторона квадрата равна 6.

47. Расстояние между параллельными прямыми равно 12. На одной из них лежит точка С, а на другой – точки А и В, причем треугольник АВС – остроугольный равнобедренный, и его боковая сторона равна 13. Найдите радиус окружности, вписанной в треугольник АВС.

или

48. Дан квадрат со стороной 7 и окружность с центром в точке радиуса 2. Найдите радиус окружности, касающейся окружности , содержащейся внутри квадрата и касающейся двух его соседних сторон.

3, или , или

49. Сторона равностороннего треугольника равна 10. Точка лежит на прямой так, что . Окружности, вписанные в каждый из треугольников и , касаются прямой в точках и соответственно. Найдите длину отрезка .

или

50. В прямоугольном треугольнике АВС угол С прямой, один из углов равен . Из вершины прямого угла проведена медиана СМ. В треугольник АВС вписана окружность с центром в точке О. Найдите угол между ОМ и ОВ.

или

51. Дан параллелограмм АВС D . Точка М лежит на диагонали В D и делит ее в отношении 1:2. Найдите площадь параллелограмма АВС D , если площадь четырехугольника АВСМ равна 60.

52. В треугольнике АВС АВ=12, ВС=5, СА=10. Точка D лежит на прямой ВС так, что В D : D С=4:9. Окружности, вписанные в каждый из треугольников А DC и А DB , касаются стороны AD в точках E и F . Найдите длину отрезка EF .

или

53. Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найдите радиус окружности, касающейся этой прямой и сторон угла.

54. Трапеция с основаниями 14 и 40 вписана в окружность радиуса 25. Найдите высоту трапеции.

55. Вершина равнобедренного треугольника с боковой стороной 5 и основанием 8 служит центром данной окружности радиуса 2. Найдите радиус окружности, касающейся данной и проходящей через концы основания треугольника.

или

56. Окружности радиусов 20 и 3 касаются внутренним образом. Хорда АВ большей окружности касается меньшей окружности в точке М. Найдите длины отрезков АМ и МВ, если АВ=32.

24 и 8 или и

57. В окружности, радиус которой равен 15, проведена хорда АВ=24. Точка С лежит на хорде АВ так, что АС:ВС=1:2. Найдите радиус окружности, касающейся данной окружности и касающейся хорды АВ в точке С.

или

📹 Видео

Задача №16. Пересекающиеся и касающиеся окружности.Скачать

Окружность. 7 класс.Скачать

Вписанная и описанная окружность - от bezbotvyСкачать

3.32.1. Планиметрия. Гордин Р.К.Скачать

С4, егэ. Задача про три касающиеся друг друга окружностиСкачать

1 2 4 сопряжение окружностейСкачать

11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать