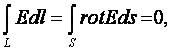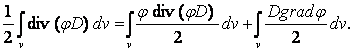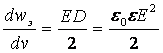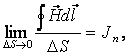Для не изменяющегося во времени (стационарного) магнитного поля ротор вектора напряженности равен вектору плотности макроскопического тока:
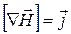
Возьмем дивергенцию от обеих частей этого соотношения:
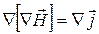
С одной стороны, дивергенция ротора всегда равна нулю, с другой — дивергенция вектора плотности тока может быть не равна нулю: в соответствии с уравнением непрерывности
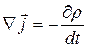
Уравнение непрерывности указывает на то, что при нестационарных процессах дивергенция плотности тока может отличаться от нуля. Например, при разряде конденсатора на резистор уменьшающийся заряда на конденсаторе является источником линий вектора плотности тока.
Максвелл предположил, что в правой части уравнения (20.40) ( 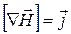
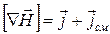
Дополнительное слагаемое он назвал плотностью тока смещения.
Определяющим свойством плотности тока смещения является условие .
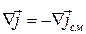
Этим обеспечивается выполнение равенства (20.41).
Из уравнения непрерывности следует, что
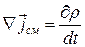
Плотность заряда связана с электрической индукцией (электрическим смещением) соотношением:
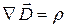
Продифференцируем это соотношение по времени и поменяем порядок дифференцирования по времени и координатам:
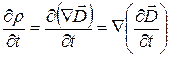
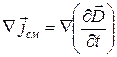
Тогда можно утверждать, что
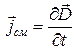
Соответственно ротор напряженности магнитного поля
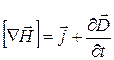
Это уравнение является одним из основных в теории электромагнитного поля.
Таким образом, ток смещения по существу представляет собой фактически изменяющееся во времени электрическое поле. Из всех свойств, присущих собственно электрическому току, для тока смещения характерна только одно — способность создавать магнитное поле. Ток смещения присутствует и в обычных проводниках, если в них имеется изменяющееся во времени электрическое поле. Однако в проводниках его плотность пренебрежимо мала по сравнению с плотностью обычного тока.
Дата добавления: 2015-09-14 ; просмотров: 593 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Александр Чирцов: ротор, дивергенция и градиентСкачать

Введение (стр. 8 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 |
и называется двусторонним.
Функция f(t) в соответствии с формулой (8.7) представляет собой сумму бесконечно большого числа гармонических составляющих. У этих составляющих в отличие от гармоник периодических функций амплитуды бесконечно малы, а частоты принимают все значения в диапазоне 0—
Функцию 
9. ОСНОВНЫЕ ПОНЯТИЯ И МОДЕЛИ ТЕОРИИ
9.1. Основные понятия и определения
Если физическое состояние каждой точки в некотором пространстве характеризуется присущим данной точке значением той или иной векторной (или скалярной) величины, то говорят, что в этом пространстве существует векторное (или скалярное) математическое поле.
 |
Поток вектора. Представим себе некоторый объём в пространстве, ограниченный замкнутой поверхностью. Малый элемент этой поверхности можно считать плоским и изобразить в виде вектора ds, нормального к нему. Положительное направление вектора элемента поверхности обычно связывается правилом правоходового винта с направлением обхода контура, ограничивающего элемент. Будем считать положительным направление обхода против часовой стрелки, если смотреть на элемент поверхности снаружи (рис.9.1). Пусть рассматриваемый объём находится в поле вектора Е; в пределах очень малого элемента поверхности вектор Е можно считать постоянным.
Скалярное произведение Eds=Eds cos(E, ds) называется элементарным потоком вектора Е через площадку ds. Интеграл этой величины, взятый по всей поверхности, окружающей рассматриваемый объём, 
Поток является скалярной величиной. Вычисление потока может производиться также и через какую угодно незамкнутую поверхность.
 |
Векторное поле можно охарактеризовать системой линий поля, проведенных так, что вектор в любой точке будет направлен по касательной к такой линии (рис.9.2). Такие линии называются силовыми линиями. Густота силовых линий поля может быть выбрана так, чтобы в известном масштабе соответствовать значению вектора. В таком случае поток вектора можно условно представить количеством линий поля, пронизывающих рассматриваемую поверхность.
Дивергенция вектора. Полный поток вектора через замкнутую поверхность, ограничивающую малый объём, может быть равен нулю или же отличаться от нуля.
В первом случае в объёме не содержится ни источника, ни стока (некоторого физического объекта, в котором линия поля могла бы начинаться или заканчиваться). Ограничивающая объём замкнутая поверхность может, однако, оказаться дважды пронизанной линией поля, идущей от источника, расположенного вне данного объема, к стоку, также находящемуся вне его.
Во втором случае внутри объёма находится либо источник, либо сток.
Предел, к которому стремится отношение полного потока вектора через замкнутую поверхность к величине ограничиваемого ею объёма при бесконечном уменьшении последнего, называется дивергенцией или расходимостью вектора

Дивергенцию вектора в какой-либо точке можно условно охарактеризовать числом линий поля, начинающихся или заканчивающихся в малом объеме, центрированном в данной точке.
Дивергенция является скалярной величиной и она положительна, если линия поля начинается в малом объёме, или отрицательна, если линия поля в этом объёме заканчивается.
 |
Физическая сущность понятия дивергенции поясняется следующими примерами: на рис. 9.3,а показан отрезок трубы, по которой протекает вода. Рассмотрим векторное поле скорости течения воды v. Поток вектора скорости через какую-либо поверхность равен объёму жидкости, протекающей через эту поверхность в единицу времени. Поток через замкнутую поверхность s равен нулю, поскольку количество жидкости, находящейся в объёме, ограниченном такой поверхностью, неизменно. Это следует из свойства практической несжимаемости воды. Следовательно, дивергенция скорости течения воды в трубе равна нулю.
На рис. 9.3,б показан отрезок трубы, закрытой с левого конца. Вначале труба была закрыта крышкой и с правого конца, а внутрь трубы накачали газ до некоторого давления выше атмосферного. Затем крышку с правого конца трубы сняли и сжатый газ стал выходить в атмосферу. Если движение газа в трубе представить векторным полем скоростей v, то дивергенция (расходимость) скорости не будет равна нулю, так как общее количество газа в каком-нибудь выделенном внутри трубы объёме s, очерченном пунктирной линией, с течением времени не остается постоянным, а уменьшается вследствие расширения газа.
 |
Циркуляция вектора. Представим некоторую площадь S, ограниченную контуром Г, и равную сумме площадей S1 и S2, ограниченных контурами Г1 и Г2 (рис.9.4). Вектор а направлен по касательной к элементу пути dl. Циркуляцией вектора а называют величину

Циркуляция обладает свойством аддитивности. Это означает, что сумма циркуляции по контурам Г1 и Г2, равна циркуляции по контуру Г, ограничивающему поверхность S. Действительно, циркуляция C1 по контуру, ограничивающему поверхность S1, может быть представлена как сумма интегралов

Первый интеграл берется по участку I внешнего контура, второй — по общей границе поверхностей S1 и S2 в направлении 2—1. Аналогично, циркуляция С2 по контуру, ограничивающему поверхность S2, равна

Первый интеграл берется по участку II внешнего контура, второй — по общей границе поверхностей S1 и S2 в направлении 1—2. Циркуляция по контуру, ограничивающему суммарную поверхность S, может быть представлена в виде

Вторые слагаемые в выражениях (9.1) и (9.2) отличаются только знаком. Поэтому сумма этих выражений оказывается равной выражению (9.3). Таким образом,

Доказанное соотношение не зависит от формы поверхностей и справедливо при любом числе слагаемых. Следовательно, если разбить произвольную поверхность S на большое число элементарных поверхностей DS (рис.9.5), то циркуляция по контуру, ограничивающему S, может быть представлена как сумма элементарных циркуляции DС по контурам, ограничивающим DS:
 |

 |
Ротор (вихрь) вектора. Предел отношения полученной величины циркуляции к величине площадки DS, при беспредельном уменьшении площадки, является вектором, который обозначается символом rot а и называется ротором (вихрем) вектора а

Знак ротора определяется правилом правоходового винта. Если винт поворачивать в плоскости контура циркуляции в направлении, показанном на рис.9.5, то поступательное движение за плоскость чертежа будет указывать направление ротора.
9.2. Потенциальные и вихревые поля
Написание формул векторного анализа значительно упрощается и облегчается, если ввести векторный дифференциальный оператор, обозначаемый символом 

Сам по себе этот вектор смысла не имеет. Он приобретает смысл в сочетании со скалярной или векторной функцией, на которую он символически умножается. Так, если умножить вектор 

который представляет собой градиент потенциала j.
Если вектор 

который есть не что иное, как дивергенция вектора а. Наконец, если умножить 

Таким образом, существует два способа обозначений градиента, дивергенции и ротора:



Векторное произведение любого вектора на самого себя равно нулю. Этот вывод можно распространить и на «вектор»

Поэтому ротор градиента скалярной величины всегда равен нулю

Векторная величина М, не имеющая ротора, является градиентом некоторого скаляра, обычно называемого скалярным потенциалом поля вектора М. Отсутствие ротора показывает, что линии поля не образуют замкнутых кривых (вихрей). Каждая линия принципиально разомкнута, начинаясь у некоторого «источника» и заканчиваясь у некоторого «стока». В точках расположения источников и стоков дивергенция вектора не равна нулю. Это — второе условие существования безвихревого (потенциального) поля.
Итак, потенциальное поле характеризуется: 1) отсутствием ротора; 2) наличием дивергенции, хотя бы в некоторых точках; 3) наличием скалярного потенциала:



Примером безвихревого (потенциального) поля является электростатическое поле, где источниками и стоками являются соответственно положительные и отрицательные заряды.
Дивергенция ротора любого вектора всегда равна нулю

Отсутствие дивергенции является первым необходимым условием существования вихревого (соленоидального) поля.
Действительно, при 

Итак, соленоидальное вихревое поле характеризуется: 1) отсутствием дивергенции; 2) наличием ротора, хотя бы в некоторых точках; 3) отсутствием скалярного потенциала:


Примером вихревого поля является магнитное поле в толще проводника с током, материал которого имеет конечное значение удельной проводимости.
Вихревое поле может быть охарактеризовано функцией, называемой векторным потенциалом (не существовавшей в случае потенциального поля).
Векторная величина В, не имеющая дивергенции, всегда может рассматриваться как ротор другого вектора А.
Если 

Вектор А называется векторным потенциалом поля вектора В.
В физических задачах обычно рассматриваются векторные величины, нигде не обращающиеся в бесконечность. Таков, например, вектор магнитной индукции В, значения которого всегда конечны.
Поэтому векторный потенциал магнитного поля А является непрерывной функцией, плавно изменяющейся при переходе от одной точки к другой, соседней.
9.3. Основные величины электростатического поля
Электромагнитное поле является особым видом материи, оно является носителем энергии и обладает характерными для него электрическими и магнитными свойствами.
Электростатическое поле представляет собой частный вид электромагнитного поля. Оно создается совокупностью электрических зарядов, неподвижных в пространстве по отношению к наблюдателю и неизменных во времени.
Электростатическому полю присуща способность воздействовать на помещенный в него электрический заряд с механической силой, прямо пропорциональной величине этого заряда.
В основу определения электростатического поля было положено механическое его проявление. Оно нашло свое выражение в известном из курса физики законе Кулона (1785).
Закон Кулона. Два точечных заряда q1 и q2 в вакууме взаимодействуют друг с другом с силой F, прямо пропорциональной произведению зарядов q1 и q2 и обратно пропорциональной квадрату расстояния R между ними. Эта сила направлена по линии, соединяющей точечные заряды. Если заряды имеют одинаковые знаки, то они стремятся оттолкнуться друг от друга, а если заряды имеют противоположные знаки, то они стремятся сблизиться:

 |
где R0 – единичный вектор, направленный по линии соединяющей заряды (рис.9.6), а 
Главными характеристиками электростатического поля являются напряженность поля Е (в вольтах на метр) и потенциал j (в вольтах). Напряженность поля равна градиенту потенциала, взятому с отрицательным знаком (рис.9.7),

 |
Если в электростатическое поле поместить настолько малый (неподвижный) положительный заряд q, что он своим присутствием не вызовет сколько-нибудь заметного перераспределения зарядов на телах, создающих поле, то отношение силы, действующей на заряд, к величине заряда q и определяет напряженность поля в данной точке
Cледовательно, напряженность численно равна силе, действующей на единичный заряд.
В том случае, когда поле создается несколькими зарядами (q1, q2, q3,….) напряженность поля равна геометрической сумме напряженностей от каждого из зарядов в отдельности:

т. е. при расчёте электростатического поля применим метод наложения.
Линейный интеграл напряженности электростатического поля по произвольному пути между двумя точками М и N равен разности потенциалов этих точек

От формы пути величина интеграла не зависит. Очевидно, что при замкнутой форме пути линейный интеграл, т. е. циркуляция вектора Е, равен нулю; этим доказывается безвихревой характер электростатического поля.
Величина напряжённости поля важна для оценки так называемой электрической прочности изоляционных материалов. Например, для воздуха критическая напряжённость электростатического поля равна ЕКР=3
Значения потенциала j и напряжённости поля Е зависят от свойств среды; это обстоятельство учитывается посредством абсолютной диэлектрической проницаемости eа, равной произведению

где e – относительная диэлектрическая проницаемость.
В некоторых случаях желательно иметь оценку действия зарядов вне зависимости от свойств среды. Это достигается введением в расчеты вектора электрического смещения (электрической индукции)

Размерность вектора D – к /м2.
Ёмкость. Если два каких-либо проводника разделены диэлектриком и несут на себе равные по величине и противоположные по знаку заряды q, то в пространстве между ними создается электростатическое поле. Пусть разность потенциалов между телами равна U.
Под емкостью С между двумя телами, на которых имеются равные и противоположные по знаку заряды, принято принимать абсолютную величину отношения заряда на одном из тел к напряжению между телами U

Из определения ёмкости следует единица её размерности 1к/в = 1 фарада (ф). Это очень крупная единица, и потому на практике пользуются более мелкими кратными ей единицами: микрофарадой (мкф) и пикофарадой (пф).
Устройства, предназначенные для получения определенной величины емкости, называют конденсаторами. Однако, емкостью обладают не только устройства, созданные специально для её получения. Ёмкостью обладают всякие два проводящих тела, разделенных диэлектриком. Например, ёмкость двухпроводной линии равна: 
Теорема Гаусса. Из опыта известно, что если точечный заряд q поместить в центр сферы радиусом r, то числовое значение вектора смещения D в любой точке сферической поверхности будет одним и тем же и равным 

где dW – телесный угол, под которым видна из центра элементарная площадка ds. Вектор площади 
Полный поток вектора смещения, пронизывающий сферическую поверхность

Если внутри некоторой замкнутой поверхности находится несколько зарядов, то, применяя принцип наложения, найдем, что полный поток, пронизывающий замкнутую поверхность, равен алгебраической сумме зарядов, заключенных внутри неё

Это — интегральная форма теоремы Гаусса.
Введем понятие объемной плотности заряда r (т. е. заряда, приходящегося на единицу объёма [к/М3]). Сумма всех зарядов, стоящих в правой части выражения (9.4), превратится в интеграл 


Обa интеграла взяты по одному и тому же объёму, занимаемому полем. Равенство справедливо при любой величине и конфигурации этого объёма.
Поэтому подынтегральные выражения равны

Это — дифференциальная форма теоремы Гаусса.
9.4. Основные величины поля электрического тока
Электрическим полем будем называть частный случай электромагнитного поля, распространяющегося внутри объёма электропроводящих сред.
Ток проводимости. Если под воздействием внешних источников в проводящей среде (металлических проводниках, земле, жидкостях и т. д.) создано электрическое поле, то в ней будет протекать электрический ток. Электрический ток представляет собой упорядоченное движение заряженных частиц под действием электрического поля.
Носителями зарядов в металлах являются свободные электроны, носителями зарядов в жидкостях являются ионы.
Упорядоченное движение свободных электронов в металле и ионов в жидкости под действием электрического поля принято называть током проводимости.
Плотность тока проводимости d — векторная величина, направленная по движению положительных зарядов. Значение d выражает количество зарядов, проходящих в течение одной секунды через малую площадку, перпендикулярную направлению движения зарядов, отнесенное к единице её поверхности. Размерность плотности тока 
Величиной электрического тока через какую-либо поверхность является поток вектора плотности тока, взятый по этой поверхности,

Ток проводимости понимается как движение «облака» свободных зарядов в проводящей среде под действием сил электрического поля сквозь ионную решётку, препятствующую движению зарядов. Групповая скорость такого облака зарядов в металлических проводниках бывает порядка нескольких сантиметров в секунду, а скорость отдельных заряженных частиц, составляющих облако, может быть довольно большой, порядка до 106 м/сек.
 |
Представим себе малый параллелепипед с ребром Dl вдоль направления движения зарядов, имеющий площадь поперечного сечения Ds (рис.9.8). Движение зарядов происходит под действием электрического поля. Вектор напряженности поля Е совпадает по направлению с вектором плотности тока проводимости dпр.
Выберем размеры параллелепипеда Dl и Ds настолько малыми, чтобы значения Е и dпр в его пределах можно было считать постоянными.
Тогда величина тока

Напряжение, действующее вдоль ребра Dl,

Проводимость параллелепипеда определится из соотношения

С другой стороны проводимость можно определить по известной формуле

где r – удельное сопротивление [


Сравнение формул (9.5) и (9.6) приводит к зависимости, называемой законом Ома в дифференциальной форме,

Закон Ома применим к металлическим и многим жидкостным проводникам с постоянным значением удельной проводимости, однако его нельзя применять к нелинейным средам, как, например, карборунд, уголь.
Рассмотрим некоторый объём внутри проводника (рис. 9.9), окруженный замкнутой поверхностью S. Через одну часть этой поверхности S1 заряды входят в объём, через другую её часть S2 такое же количество зарядов выходит из объёма. В условиях установившегося режима общее количество зарядов, заключённых в рассматриваемом объёме, постоянно.
 |
Следовательно, поток вектора плотности тока проводимости по замкнутой поверхности равен нулю

Применяем теорему Остроградского-Гаусса

Поскольку интегрирование проводится по объёму конечных размеров, причём равенство нулю сохраняется при любой конечной величине и форме объёма, то подынтегральное выражение должно равняться нулю

Это первый закон Кирхгофа (точнее, закон Кирхгофа—Ленца) в дифференциальной форме. Он выражает то, что линия поля плотности установившегося тока проводимости нигде не начинаются и не заканчиваются, т. е. всегда замкнуты; иначе говоря, поле плотности тока проводимости имеет либо вихревой, либо смешанный характер.
Уравнение (9.7) называется уравнением непрерывности.
Ток смещения. Допустим, что плотность зарядов r внутри объёма (рис. 9.9) возрастает во времени со скоростью дr/дt. Теперь дивергенция плотности тока проводимости не равна нулю, так как каждый новый элементарный заряд, входящий в объём, является концом или началом линии поля (в зависимости от знака заряда). Поток вектора плотности тока проводимости через замкнутую поверхность, ограничивающую объём, теперь будет равен увеличению количества зарядов в объёме

Знак минус указывает, что при возрастании количества зарядов внутри объёма поток вектора плотности тока, входящий в объём, больше выходящего.
Заменяем левый интеграл по теореме Остроградского—Гаусса

Оба равных интеграла взяты по одному и тому же объёму. Равенство сохраняется при любой конечной величине и форме объёма, следовательно, подынтегральные выражения равны друг другу

Применяя теорему Гаусса в дифференциальной форме

Поскольку порядок проведения операций дифференцирования не играет роли, меняем местами символ дифференцирования по времени и символ дивергенции; последний выносим за скобки

Выражение (9.8) является более общей формой первого закона Кирхгофа. Второй член в скобках представляет собой плотность тока смещения: её величиной оценивается скорость изменения по времени электрического поля, сопровождаемого таким же магнитным эффектом, как и ток проводимости.
Делаем замену D=eaE и, используя закон Ома в дифференциальной форме, получаем

Выражение в скобках представляет собой полную плотность тока

Её поле является вихревым или смешанным, так как дивергенция равна нулю.
Линии полной плотности тока не имеют поэтому ни начал, ни концов, т. е. всегда образуют замкнутые кривые. Простым примером служит цепь зарядки конденсатора от источника постоянной э. д.с. Ток проводимости в соединительных проводах, плотность которого dпр, доставляет заряды из источника на обкладки конденсатора, а в диэлектрике конденсатора нарастает электрическое поле со скоростью дD/дt, равной плотности тока смещения dсм.
9.5. Основные величины магнитного поля
Магнитная индукция В — векторная величина, определяемая из закона Ампера о силе взаимодействия dF линейного элемента тока I dl с исследуемым магнитным полем (рис. 9.10),

 |
Величина В измеряется в н/а м = в ceк/м 2= тл. В физике часто оперируют с единицей, в 10000 раз меньшей, называемой гауссом.
Для большей наглядности в описание магнитных процессов вводят понятие линий магнитной индукции, т. е. воображаемых линий в пространстве, проведённых так, что касательная к линии в каждой точке совпадает по направлению с вектором магнитной индукции.
Интеграл вектора магнитной индукции по некоторой поверхности называется магнитным потоком через эту поверхность

Магнитный поток измеряется в вольт-секундах (веберах). Он является скалярной величиной. Величину магнитной индукции В можно рассматривать как плотность магнитного потока.
Закон Био-Савара. Экспериментальная зависимость между током и создаваемой им напряжённостью магнитного поля впервые была получена Био и Саваром в 1820 г. Если в замкнутом линейном контуре протекает ток I, то по закону Био-Савара элементарный вектор магнитной индукции в некоторой точке пространства (в „точке наблюдения»), определяемый элементом тока 
 |

 |
здесь dl — длина элемента проводника (рис.9.11); направление элемента dl совпадает с положительным направлением тока; 1r — единичный вектор, направленный из указанного элемента проводника в точку наблюдения; r — расстояние между отрезком проводника и точкой наблюдения.
В формулу (9.9) входит абсолютная магнитная проницаемость mа, характеризующая среду. Для вакуума и воздуха значение абсолютной магнитной проницаемости практически принимается равным магнитной постоянной
Величина m0 равна отношению линейного интеграла вектора магнитной индукции по замкнутому контуру в вакууме к электрическому току, проходящему сквозь поверхность, ограниченную этим контуром.
Группа так называемых ферромагнитных материалов, играющих первостепенное значение в электромашиностроении и аппаратостроении (сталь, никель, кобальт и их сплавы), обладает иными значениями абсолютной магнитной проницаемости; обычно её выражают так:

где m — относительная магнитная проницаемость, т. е. безразмерный коэффициент, показывающий, во сколько раз магнитная проницаемость данного материала больше магнитной постоянной.
У некоторых материалов (сплавы железа с никелем, называемые пермаллоями, или железо, отожженное в водороде) величина m при определённых условиях достигает сотен тысяч.
Полная величина магнитной индукции в данной точке выражается интегралами

Интегрирование производится в первом случае по всему замкнутому контуру тока, состоящему из элементов Idl, а во втором случае — по всему объёму V, занимаемому током, т. е. заполненному элементами 
Если хотят охарактеризовать магнитный эффект тока I вне зависимости от среды, то рассматривают векторную величину Н=В/mа, называемую напряжённостью магнитного поля и измеряемую в а/м.
Линия в пространстве, к которой вектор Н касателен в любой точке, называется линией напряжённости магнитного поля. В неферромагнитной среде эти линии совпадают с линиями магнитной индукции.
Основной закон магнитного поля — закон полного тока.. Закон полного тока выражает те же опытные факты, что и закон Био-Савара, однако в форме, значительно более удобной для практики. Формулируется он так: в любом магнитном поле линейный интеграл от напряжённости магнитного поля вдоль любого замкнутого контура равен полному току, проходящему через любую поверхность, ограниченную этим контуром, т. е.


Это интегральная форма первого уравнения Максвелла.
Под полным током понимают весь ток (ток проводимости и ток смещения), пронизывающий контур интегрирования.
Интегральная форма закона полного тока применяется, когда может быть использована симметрия в поле. Так, например, напряжённость поля в некоторой точке А в поле уединённого прямого провода с током I (рис.9.12) по закону полного тока определится следующим образом: проведём через точку А окружность радиуса R в плоскости, перпендикулярной оси провода, так что центр её находится на оси провода. В силу симметрии напряжённость поля во всех точках окружности численно одна и та же. Направление напряжённости совпадает с касательной к окружности. Поэтому
 |

Таким образом, с увеличением радиуса R напряжённость магнитного поля убывает по гиперболическому закону H=I/2pR.
Преобразуем по теореме Стокса [


Последнее выражение представляет собой первое уравнение Максвелла в дифференциальной форме.
В любом месте пространства, где существует ток проводимости или ток смещения (или оба тока совместно), имеется вихревое (имеющее ротор) магнитное поле.
Закон Фарадея. Этот закон называется законом электромагнитной индукции. Он утверждает, что в цепи, охватывающей изменяющийся во времени магнитный поток, возникает э. д.с., пропорциональная скорости изменения потока, т. е.

С другой стороны э. д.с. е может быть выражена как линейный интеграл напряжённости электрического поля

Применяя к (9.12) теорему Стокса, получим

Из (9.11) и (9.13) окончательно имеем:

Это есть второе уравнение Максвелла, представляющее собой дифференциальное выражение закона электромагнитной индукции. Физическое содержание второго уравнения Максвелла состоит в том, что в пространстве, где магнитная индукция изменяется во времени, появляется напряженность электрического поля. Направление линий напряженности электрического поля связано с изменением магнитной индукции правилом левоходового винта.
9.6. Передача энергии в электрических цепях.
Передача энергии на расстояние в электрических цепях осуществляется посредством электромагнитного поля. Примерами служат распространение света и радиоволн.
Исследование таких процессов передачи энергии производится на основе учения о движении энергии, разработанного к 1874 г. Аналогичное исследование электромагнитного поля было сделано Пойнтингом в 80-х годах XIX в.
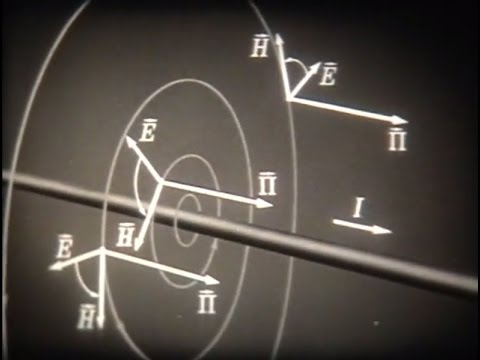
Вектор Пойнтинга (вектор потока или излучения энергии) определяется векторным произведением векторов Е и Н: П = [EH], где E и H векторы напряжённости электрического и магнитного полей соответственно, определяет энергию, проходящую в единицу времени через единичную площадку, перпендикулярную его направлению. Размерность этого вектора — отношение мощности к единице поверхности, т. е. вт/м2. Мощность, проходящая через элементарную площадку dS равна ПdS (рис.9.13,а, б).
 |
Энергией обладают не заряды на проводниках, а электрическое поле, распределённое в разделяющем их диэлектрике. Мощность передаваемой энергии определяется не непосредственно током или напряжением, а связанным с ними потоком вектора Пойнтинга.
Пусть два параллельных провода проходят в направлении, перпендикулярном плоскости чертежа (рис.9.14), и при постоянном напряжении U между этими проводами ток I в верхнем проводе направлен за плоскость чертежа, а в нижнем — наоборот; в конце линии включена нагрузка. Передаваемая от генератора мощность равна

а напряжённость электрического поля между проводами
направлена от верхнего провода к нижнему.
 |
При заданном расположении проводов можно в первом приближении, пренебрегая напряжённостью поля в остальной части пространства, считать, что между параллельными поверхностями проводов магнитное поле однородно и Hb=I (закон полного тока).
Вектор Пойнтинга П = [EH] параллелен оси проводов и направлен к потребителю энергии. Его величина равна произведению абсолютных значений обоих векторов, так как вектор Е перпендикулярен Н. Поток вектора П по всему сечению S = bа при этом совпадает с прежним выражением для передаваемой мощности

Из произведения силы тока и напряжения получается то же значение мощности, что и при интегрировании вектора Пойнтинга. Таким образом, UI математически тождественно произведению ЕНS, так как эти выражения получаются одно из другого. Однако, связанные с этими выражениями физические картины совершенно различны. В первом случае мы представляем себе передачу энергии примерно так, как происходит перенос энергии текущей в трубе водой. Во втором случае, наоборот, поток энергии идет вне проводов, т. е. в диэлектрике. В случае идеальных проводников (проводник бесконечной проводимости) линии электрического поля везде нормальны к поверхности проводов; поток энергии непосредственно у поверхности проводов параллелен линии. Внутри идеального проводника не существует напряженности поля. Вследствие этого внутри проводника равен нулю и вектор потока энергии. Если проводники считать неидеальными, то в них должна существовать напряжённость поля, определяемая выражением Е = d /g. В этом случае линии электрического поля уже не перпендикулярны поверхности проводника, а несколько наклонены в направлении потока энергии (рис.9.15,а).
Найдем направление потока энергии внутри проводника, изображённого на рис.9.15,б и определим его численное значение. Вектор напряжённости магнитного поля лежит в плоскости, перпендикулярной оси провода. Вектор напряжённости электрического поля внутри проводника совпадает с направлением провода, или, точнее говоря, с направлением плотности тока в нём. Поэтому вектор потока энергии П нормален к оси проводника и направлен внутрь, так как он перпендикулярен как Е, так и Н. В случае длинного одиночного провода на его поверхности


При этом Е и Н взаимно перпендикулярны, поэтому



 |
 |

Последнее равенство определяет джоулево тепло, выделяющееся в единицу времени в проводнике длиной l .
Таким образом, показано, что через поперечное сечение проводника в аксиальном направлении энергия не протекает, так как она передается только по диэлектрику. Энергия, расходуемая для покрытия потерь в проводнике, входит снаружи (из диэлектрика) внутрь проводника перпендикулярно направлению его оси.
Литература, использованная при составлении
1. Бессонов основы электротехники.:М., «Высшая школа»,1973, 745 с. с ил.
2. Теоретические основы электротехники. Т.1. Основы теории линейных цепей. Под ред. , изд. 2-е перераб. и доп.:М., «Высшая школа», 1976, 544 с. с ил.
3. Говорков и магнитные поля, изд. 3-е перераб. и доп.:М., «Энергия», 1968, 488 с. с ил.
4. Теоретическая электротехника.:М., «Мир», 1964, 773 с. с ил.
5. Вычисления в MathCAD / . – Мн.: Новое знание, 2003. – 814 с.: ил.
Видео:Дивергенция векторного поляСкачать

Факультет Радиотехники, Радиосвязи и Телерадиовещания
“Теория электромагнитного поля. Часть 1”
по дисциплинам : “Электромагнитные поля и волны” и “Электродинамика и распространение радиоволн”
Ташкент 200 7
Данное методическое пособие предназначено для студентов, изучающих курсы “Электромагнитные поля и волны” и “Электродинамика и распространение радиоволн”
по направлениям образования: “Телевидение, радиосвязь и радиовещание” и “Радиотехника”.
В пособии приводятся основные понятия теории электромагнетизма, дается раскрытие физического смысла фундаментальных законов электродинамики – системы уравнений Максвелла в их классической интегральной и дифференциальной формах.
1.1. Электрический заряд.
1.2. Напряженность электростатического поля.
1.3. Безвихревой характер электростатического поля.
1.4. Электрический потенциал.
1.5. Графическое изображение электростатического поля.
1.6. Поляризованность диэлектрика и электрическая индукция.
1.7. Теорема Гаусса.
1.8. Проводники в электростатическом поле.
1.9. Граничные условия в электростатическом поле.
1.10 Энергия электростатического поля.
2. Ток и плотность тока проводимости.
3. Дивергенция плотности тока проводимости.
4. Закон Ома в дифференциальной форме.
5. Полный электрический ток.
6. Магнитное поле.
6.1. Основные величины, характеризующие магнитное поле.
6.2. Магнитный поток и его непрерывность.
6.3. Скалярный потенциал магнитного поля.
6.4. Векторный потенциал магнитного поля.
6.5. Граничные условия в магнитном поле.
6.6. Энергия магнитного поля.
6.7. Методы расчетов магнитных полей.
7. Система уравнений Максвелла.
7.1. Первое уравнение Максвелла.
7.2. Второе уравнение Максвелла.
7.3. Третье уравнение Максвелла.
7.4. Четвёртое уравнение Максвелла.
8. Полная система уравнений электромагнитного поля.
1.1 Электрический заряд
Электрический заряд можно считать бесконечно делимым и пользоваться понятием плотности заряда. Если заряд “q” распределен в пространстве, то объемная плотность заряда


Если заряд “q” распределен по поверхности “S”, то поверхностная плотность заряда
и суммарный заряд определяется как
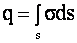
Линейная плотность заряда
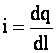
где dl — элемент линии, вдоль которой распределен заряд.

Два точечных заряда одного знака, находящиеся друг от друга на расстоянии R , отталкиваются друг от друга. Сила отталкивания “F” в вакууме определяется законом Кулона
где q1 и q2 — точечные заряды, к — коэффициент пропорциональности, определяемый как

где e 0 — электрическая постоянная, равная 8,85 . 10 -12 ф/м.
Если заряженные тела находятся в однородной изотропной среде, то

где e — относительная диэлектрическая проницаемость среды.
Сила, действующая на заряд q, в векторной форме записывается как
1.2 Напряженность электростатического поля
Предел отношения силы F, действующей на пробный заряд, к величине этого заряда q, когда он стремится к нулю, называют напряженностью электрического поля
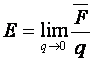
Напряженность электрического поля точечного заряда
в системе СИ [E] = [в/м].
Сила взаимодействия двух точечных зарядов
Видео:Билет №31 "Ток смещения"Скачать

 = E × q .
= E × q .
Если в поле отсутствует пробный заряд q, механическая сила взаимодействия равна нулю, но напряженность Е в каждой точке отлична от нуля.
Электрическим смещением или электрической индукцией называют величину D , которая в однородных и изотропных средах пропорциональна напряженности электрического поля:
D = e e 0 Е — в вакууме,
D = e 0 Е — в системе СИ [ D ] = [кл/м 2 ] .
Если поле создается несколькими зарядами, то общая напряженность Е в любой точке равна геометрической сумме
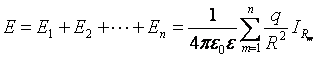
В общем случае электростатическое поле могут возбудить неподвижные объемные, поверхностные и линейные заряды. Разбив объемы V, поверхности S и линии l на элементы dV, dS, dl можно записать:
где r — объемная, s — поверхностная, t — линейная плотности зарядов.



Суммируя геометрически вектора dE 1 по V , dE2 по S, dE3 по l получим
Это уравнение позволяет вычислить Е, если известно распределение зарядов в пространстве.
Вычисление сводится к определению проекций вектора Е в такой системе координат, в которой расчеты получаются наиболее простыми.
1.3 Безвихревой характер электростатического поля
Работа, совершенная силами поля при перемещении заряда q из точки 1 в точку 2 определяется как

Работа сил поля вдоль замкнутой кривой равна нулю. Для этого необходимо доказать, что циркуляция вектора Е равна нулю
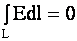
В случае точечного заряда
Так как 

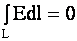
Пользуясь теоремой Стокса
Это соотношение выражает основное свойство электростатического поля — оно безвихревое.
1.4 Электрический потенциал
Так как электрическое поле безвихревое (rotE = 0), то можно найти скалярную функцию j , градиент которой, взятый со знаком “+” или “-”, равен вектору напряженности Е
В теории поля выбирают знак “-”, который указывает на то, что напряженность направлена в сторону убывания j . Скалярная функция j называется потенциальной функцией или просто потенциалом.
Потенциал любой точки
j = — ò E dl + const ,
где постоянная интегрирования определяется заданием точки с нулевым потенциалом. В системе СИ [ j ] = [в].


Разность потенциалов не зависит от формы пути интегрирования.
Потенциал поля точечного заряда

Потенциал поля неподвижных объемных, поверхностных и линейных зарядов
j = ò r dV_____ + ò s dS ___ + ò ___ t dl __ .
V 4 p e 0 e R S 4 p e 0 e R L 4 p e 0 e R
Зная потенциал, можно найти напряженность Е
Видео:#8 Ротор/Дивергенция/ГрадиентСкачать

Е = — grad j .
В поле объемных зарядов вектор Е везде конечен и непрерывен. В поле поверхностных зарядов Е конечен всюду, но претерпевает разрыв на поверхности S, по которой распределен заряд. В поле линейных зарядов вектор Е обращается в бесконечность на линии L, вдоль которой распределен заряд.
1.5 Графическое изображение электростатического поля
Электростатическое поле графически изображается с помощью эквипотенциальных поверхностей и линий вектора поля. Эквипотенциальные поверхности определяются уравнением j = const. Задавая различные значения постоянной, получают семейство поверхностей. Эквипотенциальные поверхности наносятся так, чтобы разность потенциалов двух соседних поверхностей отличалась на одну и ту же величину:
Там, где эквипотенциальные поверхности располагаются ближе, напряженность поля больше. Эквипотенциальные поверхности не пересекаются, так как потенциал — функция однозначная. Линии напряженности совпадают с касательной и пересекаются с эквипотенциальными поверхностями под прямым углом. Дифференциальное уравнение линий вектора
В декартовой системе:
Одна из эквипотенциальных поверхностей разбивается на прямоугольные площадки. Размер площадок подбирается таким образом, чтобы поток вектора поля сквозь них имел одну и ту же величину. На чертеж наносится по одной линии вектора на каждую площадку, причем так, чтобы эта линия проходила через центр площадки. В тех областях поля, в которых напряженность больше, линии вектора сгущаются. В электростатическом поле линии вектора Е разомкнутые кривые, они начинаются у положительных зарядов и заканчиваются у отрицательных.
1.6 Поляризованность диэлектрика и электрическая индукция
Изменение напряженности электрического поля в диэлектрике в “ e “ раз вызывается поляризацией диэлектрика. При наличии внешнего поля диэлектрик перестает быть нейтральным, он поляризуется. Заряды, выявившиеся при поляризации, называются свободными. Связанные заряды создают поле, напряженность которого будет направлена противоположно напряженности внешнего поля. Поэтому Е уменьшается. Степень поляризации диэлектрика характеризуется вектором поляризованности P
где КЭ — диэлектрическая восприимчивость .
Поляризованность Р показывает, на сколько электрическая индукция в данной среде отличается от электрической индукции в вакууме
Р = D — e 0 Е = e 0 ( e — 1)Е.
В системе СИ [Р] = [кл/м 2 ]
1.7 Теорема Гаусса
Поток вектора электрической индукции D сквозь произвольную замкнутую поверхность S равен алгебраической сумме свободных зарядов q, расположенных в объеме, ограниченном этой поверхностью.

Теорема Гаусса в интегральной форме
Преобразуем поток вектора электрической индукции по теореме Остроградского
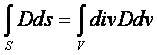
В случае объемного распределения заряда
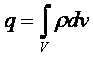
По теореме Гаусса:

Дифференциальная форма теоремы Гаусса
Объем V был выбран произвольно и равенство справедливо для всех его значений. При таком условии
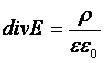
Из чего следует, что источники электрического поля находятся только в тех местах, в которых имеются электрические заряды.
1.8 Проводники в электростатическом поле
Если проводнику сообщить заряд, то под действием сил отталкивания элементы этого заряда будут перемещаться по проводнику и сосредотачиваться на его поверхности в слое, который можно считать бесконечно тонким. Напряженность Е внутри проводника равна нулю. Все точки проводника должны иметь один и тот же потенциал, то есть поверхность проводника представляет собой эквипотенциальную поверхность.
Под действием внешнего поля свободные электроны перемещаются по проводнику. На одной части сосредоточатся отрицательные заряды, на противоположной — положительные. Напряженность поля внутри проводника равна нулю. Поверхность проводника будет границей электростатического поля, которое локализовано в диэлектрике, окружающем проводник. Это используется в технике при электростатическом экранировании радиоаппаратуры.
1.9 Граничные условия в электростатическом поле
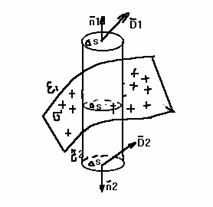
Рассмотрим границу двух непроводящих сред, диэлектрические проницаемости которых e 1 и e 2.
Пусть на границе имеется заряд с поверхностной плотностью.
Проведем замкнутую цилиндрическую поверхность S так, чтобы одна ее половина была расположена в первом диэлектрике, другая — во втором.
По теореме Гаусса
Представим поток вектора D в виде суммы трех потоков
ò D ds = ò D1 ds + ò D2 ds + ò D ds .
S D S D S S бок
Если площадка D S невелика, то можно считать, что во всех точках этой площадки вектор D имеет одну и ту же величину, тогда:
Если высоту цилиндра уменьшать так, чтобы площадки D S стремились к границе между диэлектриками, то поток через боковую поверхность будет стремиться к нулю, тогда:
D1n D S — D2n D S = s D S,
Нормальная составляющая вектора электрической индукции на границе двух непроводящих сред претерпевает скачок, равный поверхностной плотности свободных зарядов, распределенных на границе.
Нормальная составляющая вектора D на границе непрерывна. Для получения второго граничного условия проведем замкнутую линию L так, чтобы одна ее часть находилась в первом диэлектрике, другая — во втором.
Если отрезки 2-3 и 4-1 постепенно уменьшать так, чтобы в пределе они стали равными нулю, а отрезки D l совпали с граничной поверхностью, то
На границе двух непроводящих сред касательные составляющие вектора напряженности электрического поля равны.
На поверхности раздела двух сред потенциал непрерывен
Если одна из сред проводящая, то граничные условия изменятся.
Пусть первая среда — диэлектрик с проницаемостью e , вторая — проводник, тогда граничные условия запишутся:
1.10 Энергия электростатического поля
В общем случае энергия электростатического поля определяется как
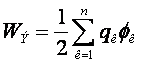
Эта формула учитывает только энергию взаимодействия. Собственная энергия точечного заряда формально равна бесконечности, так как, для того, чтобы сосредоточить заряд конечной величины в точке, надо было бы затратить бесконечно большую работу.
Этой формулой можно пользоваться, когда заряды отстоят друг от друга на расстояниях значительно больших, чем размеры тел, несущих эти заряды.
Энергия электростатического поля может быть записана

Из курса векторного анализа получаем
div ( j D) = j divD + Dgrad j .
Используя это выражение, можно записать
Так как div D = r , grad j = — E,
ò div ( j D ) dV = ò j D dS ,

D dS = — D dS = — s dS.
и энергия электрического поля
В однородных и изотропных средах
. 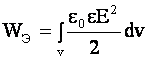
Физический смысл этого уравнения заключается в том, что носителем энергии является электрическое поле, причем энергия распределена во всем пространстве с объемной плотностью
Там, где напряженность Е отлична от нуля, силы поля могут совершать работу за счет энергии поля.
2. Ток и плотность тока проводимости
Мерой тока служит предел отношения заряда D q, проходящего сквозь заданную поверхность в течение некоторого времени D t, когда D t ® 0

Ток — величина скалярная [ i]=[A].
Плотностью тока называют векторную величину J , численное значение которой равно пределу отношения тока, протекающего через некоторую площадку, расположенную нормально к направлению движения зарядов, к величине площади этой площадки, когда она стремится к нулю, как к пределу

Направление вектора J выбирается таким образом, чтобы оно совпадало с направлением движения положительных зарядов.
Ток и плотность тока связаны соотношением

Плотность тока в системе СИ [ J ] = [ А ¤ м 2 ]
Иногда рассматривают поверхностные токи, которые протекают только по поверхности проводника
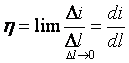
В системе СИ [ h ] = [ А ¤ м ] .
3. Дивергенция плотности тока проводимости
Постоянные токи могут быть только в замкнутых цепях. Линии вектора 

Переменные токи могут иметь место и в незамкнутых цепях. Следовательно, в переменных полях цепи с токами проводимости могут быть незамкнутыми. Там, где заканчиваются линии вектора плотности тока проводимости 
Пусть в объёме V , ограниченном поверхностью S , имеется заряд q , объёмная плотность которого равна r . Если через поверхность S выходит ток проводимости i , то заряд q станет уменьшаться и ток

Выразим ток через плотность. Получим

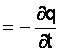

Преобразовав поток вектора 


Дивергенция плотности тока проводимости равна скорости убывания плотности объёмных зарядов. Плотность тока проводимости может иметь источники и стоки в виде изменяющихся во времени объёмных зарядов.
4. Закон Ома в дифференциальной форме
В однородном изотропном проводнике плотность тока проводимости d пропорциональна напряженности электрического поля Е
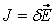
Это выражение носит название закон Ома в дифференциальной форме. Для того, чтобы в проводнике длительно проходил ток, необходимо наличие электрического поля, силы которого перемещают заряды. Такое поле может быть создано и будет поддерживаться процессами неэлектростатического происхождения (химическими, термоэлектрическими и др.), и носит название стороннего электрического поля.
Напряженность стороннего электрического поля

Напряженность результирующего поля
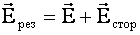
В тех областях проводника, в которых имеются сторонние силы, закон Ома записывается в виде:
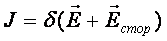
где d — удельная проводимость.
В системе СИ [ d ] = [ см/м ]
5. Полный электрический ток
Электрический ток в проводящей среде представляет собой направленное движение электрических зарядов под действием сил поля. Такой ток называется током проводимости.
Согласно закону Ома:

Если заряженное тело или частицы движутся в непроводящей среде или в вакууме со скоростью V , то они образуют ток переноса:

В молекулах диэлектрика, который вносится во внешнее электрическое поле, под воздействием сил поля связанные заряды будут смещаться и образуют ток поляризации:

где 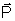
Для сред, в которых 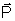

Все три перечисленные виды тока представляют собой перемещение электрических зарядов. Каждый из этих токов сопровождается магнитным полем.
Максвелл предложил назвать электрическим током изменение во времени электрического тока в вакууме
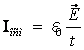
Отличие тока смещения в вакууме от других видов токов заключается в том, что он не вызывает тепловых потерь.
Полным электрическим током называется совокупность всех явлений, при которых образуется магнитное поле
Сумму тока поляризации и тока смещения в вакууме называют током смещения в диэлектрике
I см = I поляр +
Плотность тока в этом случае
I полн = I + I см = d E + 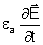
Ток переноса рассматривать не будем. В хорошо проводящей среде I >> I см, в диэлектрике с малыми потерями I см >> I . В проводящей среде токи проводимости и токи смещения соизмеримы.
6. Магнитное поле
6.1 Основные величины, характеризующие магнитное поле
Основным свойством магнитного поля является силовое воздействие его как на движущие в нём заряженные тела, так и на неподвижные проводники с электрическим током. Величиной, характеризующей магнитное поле, является вектор магнитной индукции 


Сила, действующая на линейный элемент тока, может быть определена по формуле
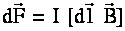
В системе СИ 
Связь между током и возбужденной им в пустоте индукции в дифференциальной форме определяется как
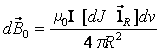
где J – плотность тока,
dV – элементарный объём,
R – расстояние от dV до точки, в которой определяется 
m 0 – магнитная постоянная m 0=4 p × 1 0 -7 Гн/м.
Если размеры поперечного сечения проводника малы по сравнению с длиной проводника и расстоянием до точки наблюдения ( проводник линейный ), можно положить
[ 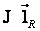

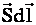
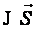
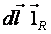

Проинтегрировав данное выражение, определим
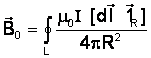
Если контур с током находится в каком-либо веществе, то величина магнитной индукции будет отличаться от 
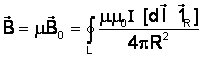
где m – относительная магнитная проницаемость среды.
Напряженность магнитного поля
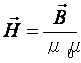
Напряжённость магнитного поля не зависит от свойств среды.
Для линейного проводника с током

Это уравнение получило название закон Био-Савара Лапласа.
Собственное макроскопическое поле вещества можно характеризовать вектором М, который называется вектором намагниченности. Этот вектор определяет, насколько магнитная индукция в данной среде 





М= k m 
где k m – магнитная восприимчивость.




следовательно, m =1+ k m.
В системе СИ [ 
6.2 Магнитный поток и его непрерывность
Поток вектора магнитной индукции записывается как
Ф= 
В системе СИ [Ф]=[Вб].
Магнитный поток сквозь замкнутую поверхность всегда равен нулю
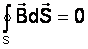
Пользуясь теоремой Остроградского, можно записать:

Это равенство справедливо для любого объёма. Следовательно,
div 
Это соотношение — дифференциальная форма принципа непрерывности магнитного потока. В любой точке магнитного поля нет ни истока, ни стока линий вектора магнитной индукции. Линии 
Количественная связь между циркуляцией вектора 

Выделим в какой-либо среде небольшой контур и составим циркуляцию вектора 
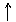











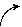







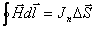




rot п 
rot 
rot 
Вектор может быть определён как функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.
6.3 Скалярный потенциал магнитного поля
Вихревыми принято называть поля, ротор которых отличен от нуля. Так как для магнитного поля постоянного тока rot 


Для таких областей:

div 

div 
или Ñ 2 j М=0 – уравнение Лапласа для областей не занятых током.
Разность скалярных магнитных потенциалов между точками 1 и 2 называют падением магнитного напряжения между точками 1 и 2
UM12= j M1 — j M2 = 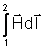
Следует различать понятия «падение магнитного напряжения» и «магнитное напряжение». Первое определяется только линейным интегралом от 
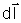
6.4 Векторный потенциал магнитного поля
Для расчёта магнитного поля используется векторный потенциал


Основанием для представления индукции в виде ротора от вектора потенциала служит то, что дивергенция любого ротора тождественно равна нулю:
div 

Векторный потенциал применяется для определения магнитной индукции для определения магнитного потока, пронизывающий какой-либо контур.
6.5 Граничные условия в магнитном поле
Для магнитного поля Н1 t =Н2 t . Это равенство выводится путём составления линейного интеграла 
со сторонами mn и pq . Длину стороны mn и pq обозначим dl . Тогда :
Следовательно, H 1 t = H 2 t . Это условие не выполняется, если на поверхности раздела двух сред протекает так называемый поверхностный ток. В этом случае:
При наличии поверхностного тока с плотностью s тангенциальная составляющая напряжённости поля терпит разрыв.
Для магнитного поля
Это вытекает из принципа магнитного потока
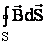
Выделим на границе раздела небольшой плоский параллелепипед и подсчитаем потоки вектора 

6.6 Энергия магнитного поля
Магнитный поток сквозь элементарную площадку dl равен: d Ф= 

Ф= 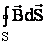
Построим в контуре, ограничивающем площадку d 


Энергия 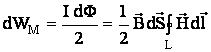
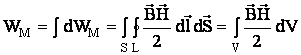
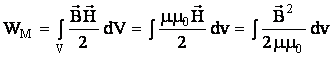
Так как 


div [ 





Тогда можно записать

По теореме Остроградского:
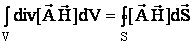
Так как магнитное поле занимает неограниченный объём, то S можно представить себе как шаровую поверхность бесконечно большого радиуса R . Вектор [ 

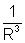
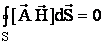
Тогда по первому уравнению Максвелла rot 


6.7 Методы расчетов магнитных полей
Расчет магнитных полей чаще всего сводится к определению вектора 
Если непосредственное определение 
💥 Видео
Дивергенция векторного поля. Гидродинамическая аналогия. Теорема Остроградского.Скачать

ДивергенцияСкачать

Билеты №12-14 "Электрический ток"Скачать

Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Александр Чирцов про дивергенцию и роторСкачать

41. Основные понятия теории векторных полейСкачать

ДивергенцияСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

45. Электрическое смещениеСкачать

Электродинамика | плотность токаСкачать

Основные физические понятия технической электродинамики, 1978Скачать
Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать

59. Магнитное поле в веществеСкачать

Лекция №10. Электростатика и магнитостатикаСкачать

60. Уравнения МаксвеллаСкачать







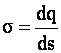


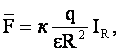
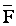 = E × q .
= E × q .