Как поделить треугольник на треугольник и четырехугольник

Задача: как разрезать треугольник двумя разрезами на три четырёхугольника и треугольник. Задача на смекалку — справится даже первоклассник, но если нужно обоснование решения, то тут придется порассуждать.

Видео:Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Решение задачи про треугольник

Для того, чтобы разрезать треугольник двумя разрезами на три четырехугольника и 1 треугольник нужно понять, что мы не можем разрезать треугольник лучами, исходящими из его вершин, потому что тогда для четырехугольников вершин будет недостаточно. Четырехугольники образованы двумя лучами, значит, каждые две стороны должны быть у них общими с соседними четырехугольниками. Таким образом общими будут 5 вершин. И три вершины — вершины треугольника. Всего получится 8 точек пересечения, одна из которых внутри треугольника, четыре на его сторонах и три — вершины треугольника. Таким образом, нарисовать такой способ разрезания треугольника двумя разрезами можно так:

Разрезать треугольник можно так

Или разрезать треугольник можно так

Или еще так можно разрезать треугольник

Главное, чтобы лучи не выходили из вершин, а давали нам дополнительные вершины для четыреухгольников. Для этого они должны пересекать стороны треугольника.

Любая из этих трех картинок — правильная. И можно нарисовать множество вариаций.

Видео:Треугольники в четырехугольники в BlenderСкачать

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Математика | 1 — 4 классы

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Смотреть во вложении.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник?

Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Как при помощи 2 отрезков разделить четырёхугольник чтобы получить три треугольника и три четырёхугольника?

Как при помощи 2 отрезков разделить четырёхугольник чтобы получить три треугольника и три четырёхугольника.

Видео:Построение пятиугольника циркулемСкачать

Как разделить четырехугольник отрезком так чтобы получился треугольник и пятиугольник?

Как разделить четырехугольник отрезком так чтобы получился треугольник и пятиугольник?

Видео:Как разрезать треугольник по двум прямым на три части, из которых можно сложить прямоугольник?Скачать

Как разделить отрезком пятиугольник на : 1 — треугольник и шестиугольник, 2 — на треугольник и пятиугольник?

Как разделить отрезком пятиугольник на : 1 — треугольник и шестиугольник, 2 — на треугольник и пятиугольник.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Нарисуйте шестиугольник ABCDKM разделите его двумя отрезками чтобы получилось 3 треугольника , 4 четырехугольника, 1 пятиугольник?

Нарисуйте шестиугольник ABCDKM разделите его двумя отрезками чтобы получилось 3 треугольника , 4 четырехугольника, 1 пятиугольник.

Видео:Периметр треугольника. Как найти периметр треугольника?Скачать

Раздели фигуру двумя отрезками на : 1) 1 треугольник и 2 четырёхугольника (фигура : четырёхугольник)?

Раздели фигуру двумя отрезками на : 1) 1 треугольник и 2 четырёхугольника (фигура : четырёхугольник).

Видео:Урок 6. Треугольники, четырёхугольники, многоугольники. ОГЭ. Вебинар | МатематикаСкачать

Разделить прямоугольник двумя линиями так чтобы получить 2 треугольника 2 четырёхугольника и2 пятиугольника?

Разделить прямоугольник двумя линиями так чтобы получить 2 треугольника 2 четырёхугольника и2 пятиугольника.

Видео:Площади фигур. Сохраняй и запоминай!#shortsСкачать

Начертите в треугольнике два отрезка так, что бы получилось два треугольника и четырёхугольник, двумя способами?

Начертите в треугольнике два отрезка так, что бы получилось два треугольника и четырёхугольник, двумя способами.

Видео:Построение медианы в треугольникеСкачать

Как провести 2 отрезка в треугольнике, чтобы получилось 2 треугольника, 1 четырёхугольник и 1 пятиугольник?

Как провести 2 отрезка в треугольнике, чтобы получилось 2 треугольника, 1 четырёхугольник и 1 пятиугольник?

Видео:Геометрия - Построение правильного треугольникаСкачать

Как разделить пятиугольник двумя линиями чтобы получилось 3 треугольника?

Как разделить пятиугольник двумя линиями чтобы получилось 3 треугольника.

На этой странице сайта размещен вопрос Как разделить треугольник двумя отрезками так, чтобы получить два треугольника, один четырёхугольник и один пятиугольник? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 1 — 4 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

1) 6 * 12 = 72 в 12 коробках 2) 5 * 15 = 75 в 15 коробках 3) 72 + 75 = 147 всего.

12 коробок по 6 кубков 15 коробок по 5 кубков Всего — ? 1) 12 * 6 = 72 (кубка) — 12 коробок 2) 15 * 5 = 75 (кубков) — 15 коробок 3) 72 + 75 = 149 (кубков) — всего Ответ : 149 кубков всего отправили.

2х — 2>5х + 1 2х — 5х>1 + 2 — 3х>3 х.

Я русский но пофиг решение (1 / х + 1 / 10) * 3 = 1 / 2 (10 + х) * 3 / 10х = 1 / 2 х = 15 первая 5 / 2 = 10 вторая ответ 10 и 15.

1)268 : 4 = 67 2)67 — 35 = 32.

Если нужно письменно(то есть с иксом)то это не ко мне. А так, во втором, так как например мороженое может стоить 35 рублей, и во 2 киоске цену поднимут сразу на 20%, то есть 35 + 10% = 42, а в первом сначала подняли на 10%, то есть 35 + 10% = 38. 5..

Во втором прорвиторг.

1) 61 * 5 = 305 (км) — проехал автомобиль за 5 часов ; 2) 73 * 7 = 511 (км) — проехал автомобиль за 7 часов ; 3) 305 + 511 = 816 (км) — весь путь автомобиля ; 4) 5 + 7 = 12 (ч) — время в пути ; 5) 816 : 12 = 68 (км / ч) — средняя скорость автомобиля ..

Видео:Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Урок геометрии «Равновеликие фигуры в решении задач»

Разделы: Математика

Цель урока:

• повторение и обобщение ключевых задач о равновеликих фигурах;
• обучение учащихся поиску решения задач в ходе создания проблемно-познавательной ситуации;
• развитие грамотной устной и письменной математической речи учащихся.

Оборудование: доска, с заготовленными чертежами или слайды; раздаточный материал: учебное пособие Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса.

Ход урока

Заканчивая изучение темы «Площади», сегодня мы повторяем и развиваем наши знания о равновеликих фигурах.

1. Чтобы вспомнить понятие «равновеликие фигуры», поиграем в «Да» и «Нет».

Я составила диктант-попурри, выбрав вопросы из ваших диктантов, связанных с этим понятием. Я читаю вопрос, его автор комментирует правильный ответ.

Учащимся к семинару по теме «Площади» было предложено домашнее задание: составить диктант из пяти вопросов по данной теме, ответы на которые предполагали либо «да», либо «нет». Данную работу можно было выполнять группами по два человека, увеличив количество вопросов. Для быстрой проверки умения оперировать с понятиями при проведении диктантов используются сигнальные карточки: треугольники белого цвета и цветные треугольники, вырезанные из бумаги, при ответе «Да» учащиеся поднимают карточку белого цвета, при ответе «Нет» — цветной треугольник.

• Верно ли, что фигуры, имеющие равные площади, называются равновеликими?
• Верно ли, что равные многоугольники равновелики?
• Верно ли, что если площади фигур равны, то и фигуры равны?
• Могут ли равновеликие фигуры быть равными?
• Верно ли, что диагонали параллелограмма делят его на четыре равновеликих треугольника?

2. Какие ключевые (базовые) задачи о равновеликих треугольниках мы рассматривали?

№1. Медиана треугольника разделяет его на два равновеликих треугольника.

Обоснуйте это утверждение (открыть заготовленный рис. №1 и по ходу обоснования сделать запись, рисунок не стирать).

№2. Все треугольники с общим основанием, вершины которых лежат на прямой, параллельной основанию, равновелики.

Обоснуйте это утверждение (открыть рис. №2 и по ходу обоснования сделать запись, рисунок не стирать).

1) На рисунке 3 я начертила ломаную ADB. Сравните площади четырёхугольников ADBС и ADBХ, ответ обоснуйте.

Вывод:

Сколько четырёхугольников равновеликих четырёхугольнику ADBC можно построить на рисунке 3?

Ответ: бесконечно много.

Что для этого надо сделать?

Ответ: отметить точку на прямойm и соединить её с точками A и B.

Полученный четырёхугольник будет равновелик четырёхугольнику ADBC.

Какой результат я могла бы получить, если бы дополнила рисунок 3 ломаной из

3-х звеньев? 4-х звеньев?

Ответ: бесконечно много равновеликих пятиугольников, шестиугольников и т.д.

Показать рисунок 4.

2) Начертите выпуклый четырёхугольник ABCD. Проведите диагональ AC. (рис.5)

Как построить четырёхугольник, равновеликий четырёхугольнику ABCD, диагональ которого есть отрезок AC?

Ответ: провести прямую а такую, что а ll АС, и D.

Пусть E, четырёхугольник ABCD равновелик четырёхугольнику ABCE.
Докажите последнее утверждение.

3) Есть ли на Рис. 6 равновеликие треугольники?

Какое утверждение позволяет нам это доказать?

Пусть .

Можно ли выразить площадь четырёхугольника ABCO через и ?

Ответ: да,

Можно ли выразить площадь четырёхугольника ABCO через ?

Ответ: да,

Как связаны ?

Ответ:

4) Решим задачу о разбиении данного выпуклого четырёхугольника на две равновеликие части.

Прочитаем условие задачи № 130 [1]

№ 130. В выпуклом четырёхугольнике ABCD через середину O диагонали BD проведена прямая, параллельная диагонали AC. Она пересекает сторону AD в точке E.

Докажите, что .

Сделаем чертёж (рис.7).

На рисунке отметим, что точка О – середина BD и укажем, что EO ll AC. Итак, что мы должны доказать? . Обозначим . Какую часть должна составлять площадь каждой фигуры от S? Проанализируем условие, подумаем: по условию точка О – середина BD, какое утверждение, связанное с равносильностью фигур, мы могли бы использовать?

Ответ: медиана делит треугольник на два равновеликих треугольника.

Что нам надо провести на чертеже, чтобы можно было это утверждение применить?

Ответ: медианы АО и СО.

1. Проведём АО и СО.
2. 
3. по свойству медианы.
4. , по свойству 2 площадей.
   Какое условие мы не использовали?
   Ответ: EO ll AC.
   Можем ли мы сравнить площади четырёхугольников ABCE и ABCO?
5. т.к. EO ll AC, то , , .
6. , , значит, по свойству 2 площадей , ч.т.д.

Итог урока

Сегодня мы посвятили урок равновеликим многоугольникам. А где это может нам понадобиться, где практически можно применить полученные знания?

Пусть пройдёт какое-то время и кому-то из вас доведётся стать землеустроителем. Всем известно, что земледельцу не важно, какой формы участок, важна его площадь.

Допустим, что надо решить задачу: разделить участок на две части, равные по площади, если участок имеет форму: а) треугольника; б) четырёхугольника, при условии, что граница должна проходить через вершину многоугольника (столб на участке, например, стоит в этой вершине, и никому не хочется иметь его на своей земле).

Как выгоднее проводить границу: в виде ломаной или в виде отрезка прямой?

Ответ: длина отрезка меньше длины ломаной, соединяющей его концы, значит, если граница пройдёт по отрезку, то меньше материала уйдёт на ограждение.

Сформулируйте поставленную задачу на языке геометрии.

Ответ: а) Разделить треугольник на две равновеликие части прямой, проходящей через его вершину.

Как это сделать?

Ответ: Провести медиану из этой вершины.

Ответ: б) Разделить четырёхугольник на две равновеликие части прямой, проходящей через его вершину.

Как это сделать?

Решить задачу №130.

1. Провести АС.
2. Провести ВD.
3. Отметить точку О середину ВD.
4. Провести прямую mтакую, чтоm ll AC,
5. m пересекает CD в точке М
6. АМ – искомая граница.

Как разделить на две равновеликие части участок, имеющий форму пятиугольника?

Литература

1. Атанасян Л.С. и др. Геометрия: дополнительные главы к школьному учебнику 8 класса. М.: Просвещение, 1996.

💡 Видео

Задание № 15. ОГЭ - 2021. ТРЕУГОЛЬНИКИ и ЧЕТЫРЕХУГОЛЬНИКИСкачать

Задача, которая поставила маму первоклассника в тупикСкачать

Задача на логику как разрезать на две части и получить квадрат?Скачать

Правильные треугольник, четырехугольник и шестиугольник (вывод основных формул)Скачать

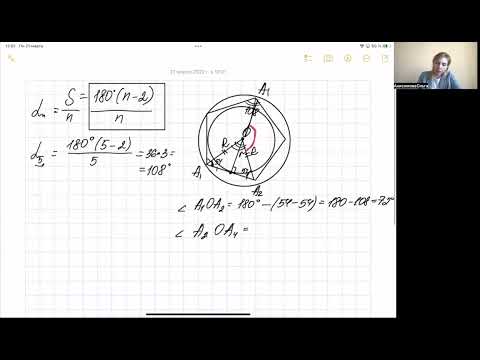
Тема 15. Правильный треугольник, четырехугольник, шестиугольникСкачать

Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать