Если посмотреть на числовую окружность , то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(() (frac) (;2π)) — четвертая четверть
- Почему так важно определять какой четверти принадлежит угол?
- Про непостоянство четвертей:
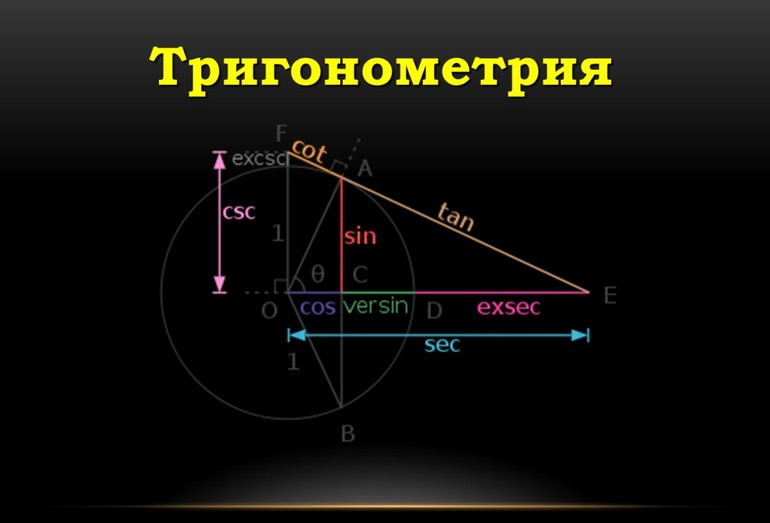
- Тригонометрический круг. Основные значения тригонометрических функций
- Знаки тригонометрических функций по четвертям — примеры определения
- Общая информация
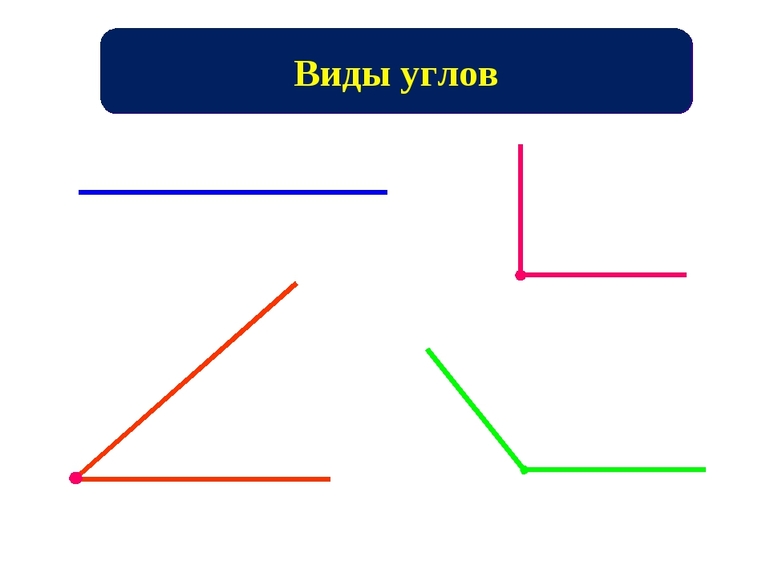
- Виды углов
- Смысл функций
- Определение знака
- Дополнительные сведения
- Построение окружности
- Свыше 2ПИ
- 🎬 Видео
Видео:В какой четверти находится точка единичной окружности, полученная при повороте Ро(1;0) на угол...Скачать

Почему так важно определять какой четверти принадлежит угол?
Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций .
Например, для любого угла из второй четверти — синус положителен, а косинус , тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.
Пример (ЕГЭ):
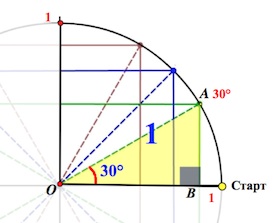
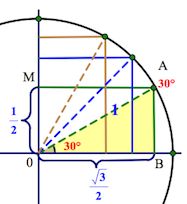
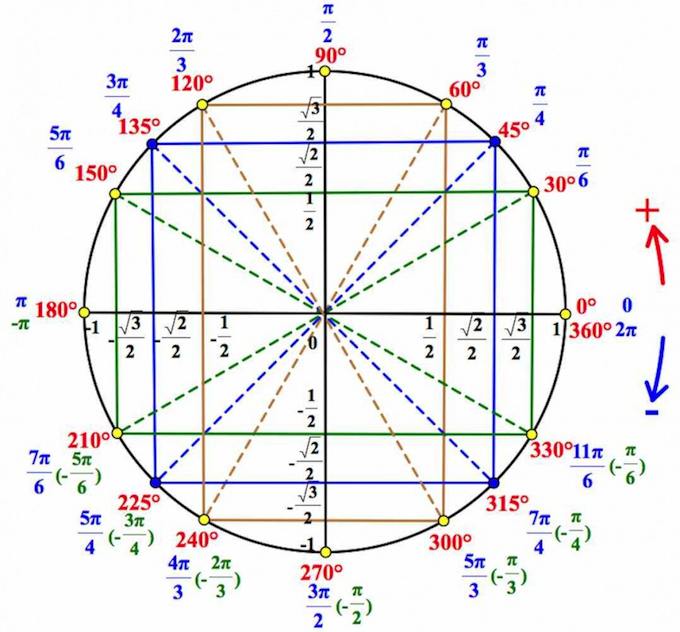
 ((0;-) (frac) ()) — четвертая четверть Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную. Видео:Как искать точки на тригонометрической окружности.Скачать  Тригонометрический круг. Основные значения тригонометрических функцийЕсли вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг : Мы же здесь будем все подробно разбирать шаг за шагом + показать Тригонометрический круг – не роскошь, а необходимость Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений. Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки! Нас выручит тригонометрический круг ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ! К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, Никак. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как! А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда. Знакомство с тригонометрическим кругомДавайте по порядку. Сначала выпишем вот такой ряд чисел: И, наконец, такой: Конечно, понятно, что, на самом-то деле, на первом месте стоит Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку». И зачем оно нам? Эта цепочка – и есть основные значения синуса и косинуса в первой четверти. Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной). От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы
Это почему же, спросите вы? Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями. Треугольник АОВ – прямоугольный, в нем Значит, АВ= Надеюсь, уже что-то становится понятно? Так вот точка В и будет соответствовать значению Аналогично с остальными значениями первой четверти. Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . Про тангенс и котангенс позже. Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения. Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг , без которого никуда в тригонометрии. А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье. Видео:Найти знак тригонометрической функции (bezbotvy)Скачать 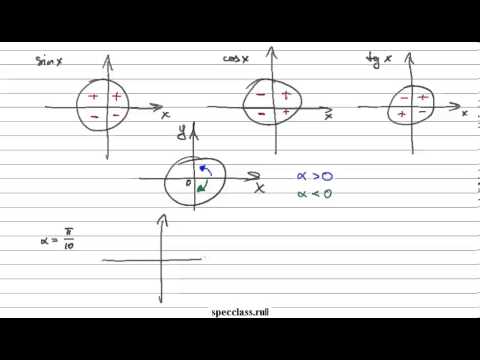 Знаки тригонометрических функций по четвертям — примеры определенияВидео:Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать  Общая информацияРаздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.
Виды угловВажной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов. Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные. Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:
Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:
Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный. Смысл функцийТригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.
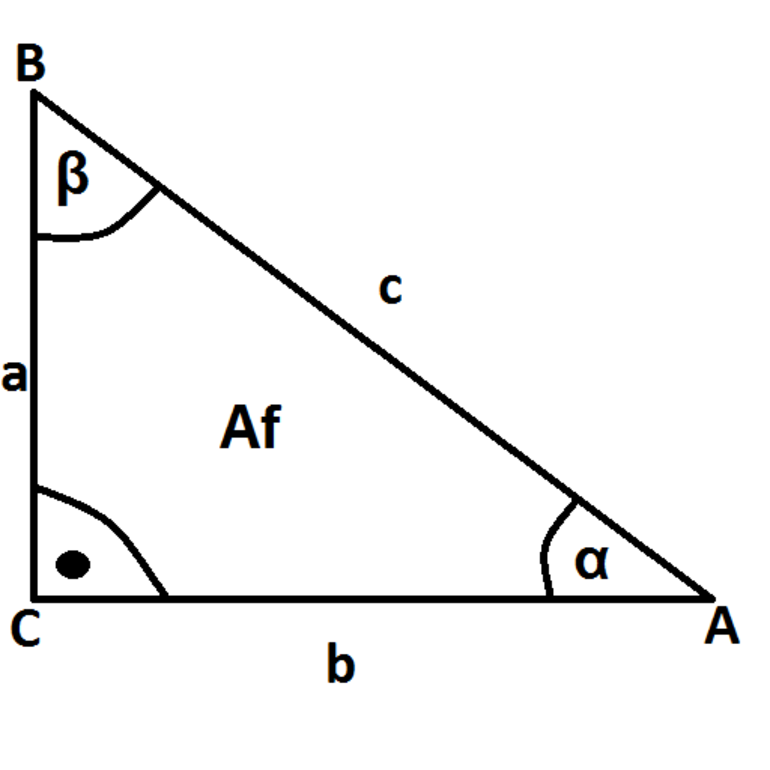
Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ. Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов. Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать  Определение знакаДостоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом. Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном. Дополнительные сведенияДля определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно). Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180. Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a). Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a). Построение окружностиСделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у». Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:
Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:
После расчетов нужно выполнить проверку знаков. В III четверти больше нуля только тангенс и котангенс. Однако бывают случаи, когда значение градусной меры угла превышает 360. Свыше 2ПИСуществует определенный тип задач, в которых величина градусной меры угла свыше 360 градусов. Например, следует вычислить значения тригонометрических функций угла -26ПИ/6. Решается она следующим образом:
Во втором, четвертом и пятом пунктах функции являются нечетными. Если посмотреть на график, то движение осуществляется по часовой стрелке, поскольку угол является отрицательным числом. Функция косинуса является четной. Ее числовое значение — положительная величина. Последним этапом считается проверка знаков. Угол находится в IV четверти. Значения функций совпадают. Таким образом, при решении задач по тригонометрии следует применять тригонометрическую окружность, с помощью которой можно безошибочно определять знак функции. 🎬 Видео10 класс, 11 урок, Числовая окружностьСкачать  Как запомнить тригонометрический круг специально ничего не выучивая?Скачать  Вычисление значений тригонометрических функцийСкачать  12 часов Тригонометрии с 0.Скачать  РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать  Знаки тригонометрических функций. 9 класс.Скачать 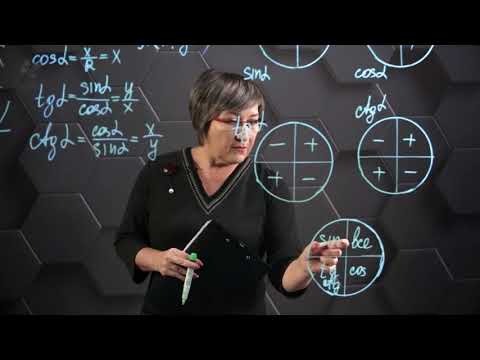 18+ Математика без Ху!ни. Формулы ПриведенияСкачать  Период тригонометрических функций тангенс и котангенс в градусах В какой четверти находится угол поСкачать  🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать  Синус косинус тангенс котангенс числа. В какой четверти находится угол поворота. Тригонометрия 8-11Скачать  Знаки синуса, косинуса, тангенса ЛекцияСкачать 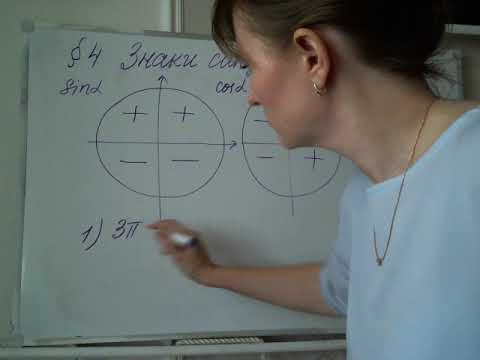 Таблица значений тригонометрических функций - как её запомнить!!!Скачать  Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать  Формулы приведения - как их легко выучить!Скачать  |


 Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…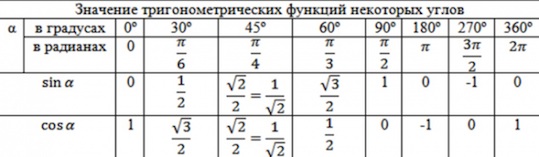
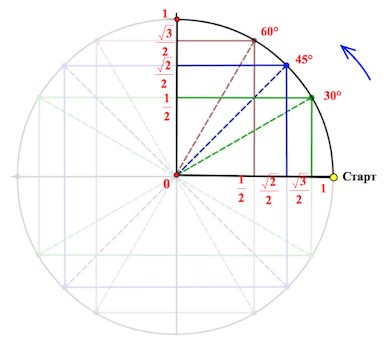 Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.