Замечательные точки треугольника интересные факты (6 видео)

Ззамечательные точки треугольника — свойства, применение и примеры решения

Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.

Итак, какие же четыре точки называются замечательными? Перечислим их:

точку пересечения медиан треугольника;

точку пересечения биссектрис треугольника;

точку пересечения высот треугольника;

точку пересечения серединных перпендикуляров сторон треугольника.

Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.

Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.

Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.

Содержание

Точка пересечения медиан треугольника
Точка пересечения биссектрис треугольника
Исследовательский проект Замечательные точки треугольника
Выберите документ из архива для просмотра:
Исследовательский проект «Замечательные точки треугольника»
Скачать:
Предварительный просмотр:
📺 Видео

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Точка пересечения медиан треугольника

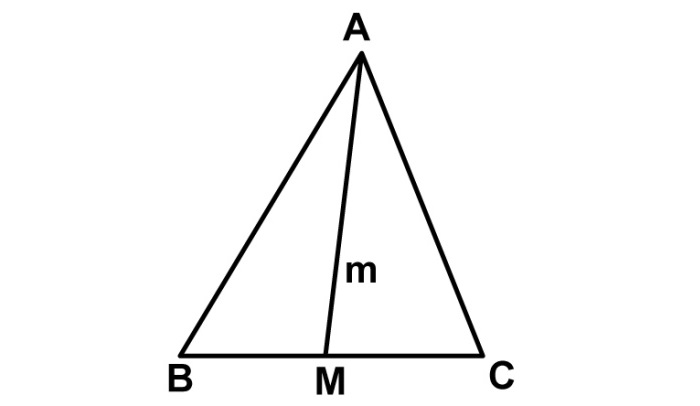
Из курса геометрии известно определение медианы треугольника.

На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.

Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.

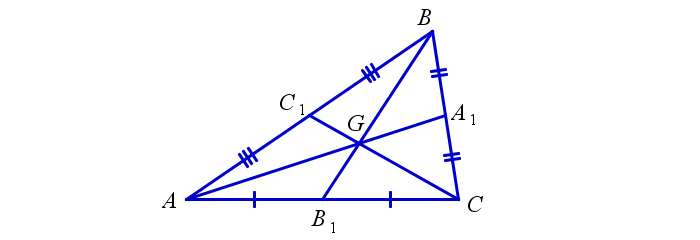
Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.

На отрезке АВ отметьте центр С₁, на стороне ВС центр А₁, на АС центр В_1.

Проведите 3 медианы из вершин. Из угла А – медиана АА₁,из угла В — медиана ВВ₁, из угла С — медиана СС_1.

Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).

Изучим следующее свойство точки пересечения трёх медиан треугольника.

Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Точка пересечения биссектрис треугольника

Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Исследовательский проект Замечательные точки треугольника

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Kurchavov_Alexandr-1.doc

Глава1. Исторические сведения о замечательных точках треугольника

1.2. Медианы треугольника

1.3. Биссектрисы треугольника

1.4. Высоты в треугольнике

1.5. Серединные перпендикуляры к сторонам треугольника

Глава 2. Исследование замечательных точек треугольника.

Список использованной литературы

Геометрия — это раздел математики, который рассматривает различные фигуры и их свойства. Геометрия начинается с треугольника. Вот уже два с половиной тысячелетия треугольник является символом геометрии; но он не только символ, треугольник — атом геометрии.

В своей работе я рассмотрю свойства точек пересечения биссектрис, медиан и высот треугольника, расскажу о замечательных их свойствах и линиях треугольника.

К числу таких точек, изучаемых в школьном курсе геометрии, относятся:

а) точка пересечения биссектрис (центр вписанной окружности);

б) точка пересечения серединных перпендикуляров (центр описанной окружности);

в) точка пересечения высот (ортоцентр);

г) точка пересечения медиан (центроид).

Актуальность: расширить свои знания о треугольнике, свойствах его замечательных точек.

Цель: исследование треугольника на его замечательные точки, изучение их классификаций и свойств.

1. Изучить необходимую литературу

2. Изучить классификацию замечательных точек треугольника

3. Уметь строить замечательные точки треугольника.

4. Обобщить изученный материал для оформления буклета.

умение находить замечательные точки в любом треугольнике, позволяет решать геометрические задачи на построение.

Глава 1. Исторические сведения о замечательных точках треугольника

В четвертой книге «Начал» Евклид решает задачу: «Вписать круг в данный треугольник». Из решения вытекает, что три биссектрисы внутренних углов треугольника пересекаются в одной точке – центре вписанного круга. Из решения другой задачи Евклида вытекает, что перпендикуляры, восстановленные к сторонам треугольника в их серединах, тоже пересекаются в одной точке – центре описанного круга. В «Началах» не говорится о том, что и три высоты треугольника пересекаются в одной точке, называемой ортоцентром (греческое слово «ортос» означает «прямой», «правильный»). Это предложение было, однако, известно Архимеду, Паппу, Проклу.

Четвертой особенной точкой треугольника является точка пересечения медиан. Архимед доказал, что она является центром тяжести (барицентром) треугольника. На вышеназванные четыре точки было обращено особое внимание, и начиная с XVIII века они были названы «замечательными» или «особенными» точками треугольника.

Исследование свойств треугольника, связанных с этими и другими точками, послужило началом для создания новой ветви элементарной математики – «геометрии треугольника» или «новой геометрии треугольника», одним из родоначальников которой стал Леонард Эйлер. В 1765 году Эйлер доказал, что в любом треугольнике ортоцентр, барицентр и центр описанной окружности лежат на одной прямой, названной позже «прямой Эйлера».

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Точки — вершины треугольника, отрезки — стороны треугольника.

В А, В, С — вершины

АВ, ВС, СА — стороны

С каждым треугольником связаны четыре точки:

Точка пересечения медиан;

Точка пересечения биссектрис;

Точка пересечения высот.

Точка пересечения серединных перпендикуляров;

1.2. Медианы треугольника

Медина треугольника ― отрезок , соединяющий вершину треугольника с серединой противоположной стороны (Рисунок 1). Точка пересечения медианы со стороной треугольника называется основанием медианы.

Рисунок 1. Медианы треугольника

Построим середины сторон треугольника и проведем отрезки, соединяющую каждую из вершин с серединой противолежащей стороны. Такие отрезки называются медианой.

И вновь мы наблюдаем, что и эти отрезки пересекаются в одной точке. Если мы измерим длины получившихся отрезков медиан, то можно проверить еще одно свойство: точка пересечения медиан делит все медианы в отношении 2:1, считая от вершин. И еще, треугольник, который опирается на острие иглы в точке пересечения медиан, находится в равновесии! Точка, обладающая таким свойством, называется центром тяжести (барицентр). Центр равных масс иногда называют центроидом. Поэтому свойства медиан треугольника можно сформулировать так: медианы треугольника пересекаются в центре тяжести и точкой пересечения делятся в отношении 2:1, считая от вершины.

1.3. Биссектрисы треугольника

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам (Рисунок 2).

Рисунок 2. Биссектриса треугольника

В произвольном треугольнике ABC проведем биссектрисы его углов. И вновь при точном построении все три биссектрисы пересекутся в одной точке D. Точка D – тоже необычная: она равноудалена от всех трех сторон треугольника. В этом можно убедиться, если опустить перпендикуляры DA 1, DB 1 и DC1 на стороны треугольника. Все они равны между собой: DA1=DB1=DC1.

Если провести окружность с центром в точке D и радиусом DA 1, то она будет касаться всех трех сторон треугольника (то есть будет иметь с каждым из них только одну общую точку). Такая окружность называется вписанной в треугольник. Итак, биссектрисы углов треугольника пересекаются в центре вписанной окружности.

1.4. Высоты в треугольнике

Высота треугольника — перпендикуляр , опущенный из вершины треугольника на противоположную сторону или прямую, совпадающую с противоположной стороной. В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника (Рисунок 3).

Рисунок 3. Высоты в треугольниках

Если в треугольнике построить три высоты, то все они пересекутся в одной точке H. Эта точка называется ортоцентром. (Рисунок 4).

С помощью построений можно проверить, что в зависимости от вида треугольника ортоцентр располагается по – разному:

у остроугольного треугольника – внутри;

у прямоугольного – на гипотенузе;

у тупоугольного – снаружи.

Рисунок 4. Ортоцентр треугольника

Таким образом, мы познакомились еще с одной замечательной точкой треугольника и можем сказать, что: высоты треугольника пересекаются в ортоцентре.

1.5. Серединные перпендикуляры к сторонам треугольника

Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

Начертим произвольный треугольник ABC и проведем серединные перпендикуляры к его сторонам. Если построение выполнено точно, то все перпендикуляры пересекутся в одной точке – точке О. Эта точка равноудалена от всех вершин треугольника. Другими словами, если провести окружность с центром в точке О, проходящую через одну из вершин треугольника, то она пройдет и через две другие его вершины.

Окружность, проходящая через все вершины треугольника, называется описанной около него. Поэтому установленное свойство треугольника можно сформулировать так: серединные перпендикуляры к сторонам треугольника пересекаются в центре описанной окружности (Рисунок 5).

Рисунок 5. Треугольник вписанный в окружность

Видео:Геометрия 8 класс. Четыре замечательные точки треугольникаСкачать

Исследовательский проект «Замечательные точки треугольника»

Знания замечательных точек и линий треугольника способствуют более эффективному и рациональному решению задач; развивают мышление и творческую активность. Изучение данной темы помогает более глубоко подготовиться к олимпиадам и ОГЭ (ЕГЭ).

Видео:Все факты о медиане треугольника для ЕГЭСкачать

Скачать:

Вложение	Размер
morozova.docx	314.9 КБ

Видео:Почему геометрия — это красиво?Скачать

Предварительный просмотр:

МБОУ «Родомановская средняя школа» Гагаринского района Смоленской области

«Замечательные точки треугольника»

обучающаяся 9 класса

Морозова Ольга

Сырокоренская Е. И.

Родоманово, 2018 г.

Объект исследования: раздел математики — геометрия.

Предмет исследования: треугольник.

Гипотеза: существует ли взаимосвязь между замечательными точками треугольника.

Цель работы: исследование треугольника на его замечательные точки, изучение их классификаций и свойств.

Изучить необходимую литературу.
Изучить классификацию замечательных точек треугольника и познакомиться с их свойствами.
Научиться строить замечательные точки.
Изучить область применения замечательных точек треугольника.
Выпустить математическую газету к предметной неделе.

Актуальность: Знания замечательных точек и линий треугольника способствуют более эффективному и рациональному решению задач; развивают мышление и творческую активность. Изучение данной темы помогает более глубоко подготовиться к олимпиадам и ОГЭ (ЕГЭ).

поисковый метод с использованием научной и учебной литературы;
практический метод решения задач;
исследовательский метод решения задач;
анализ полученных результатов.

Замечательные точки треугольника

Геометрия начинается с треугольника. Вот уже два с половиной тысячелетия треугольник является как бы символом геометрии, но он не только символ, треугольник – атом геометрии.

Треугольник неисчерпаем – постоянно открываются его новые свойства.О некоторых из них, а точнее говоря, о некоторых замечательных точках, связанных с треугольником, я расскажу в своем проекте.

Первая замечательная точка треугольника – точка пересечения биссектрис треугольника

• Биссектрисы треугольника пересекаются в одной точке.

•Точка пересечения биссектрис треугольника равноудалена от сторон этого треугольника и является центром вписанной в него окружности.

Вторая замечательная точка треугольника –точка пересечения серединных перпендикуляров к сторонам треугольника

•Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

•Точка пересечения серединных перпендикуляров к сторонам треугольника – центр описанной около него окружности.

•Центр описанной околотреугольника окружности, находится в треугольнике с острыми углами, вне треугольника с тупымуглом и на гипотенузе прямоугольного треугольника.

Третья замечательная точка треугольника — точка пересечения медиан

•Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.

•Если точку пересечения медиан треугольника соединить с его вершинами, то треугольник разобьётся на три треугольника, равных по площади.

•Важным свойством точки пересечения медиан является тот факт , что сумма векторов, началом которых является точка пересечения медиан, а концами – вершины треугольника, равна нулю.

• Точка пересечения медиан является центром тяжести треугольника.

Четвёртая замечательная точка треугольника — точка пересечения высоттреугольника

•Высоты треугольника или их продолжения пересекаются в одной точке.

•Точку пересечения высот называется ортоцентром треугольника.

Самым удивительным свойством замечательных точек треугольника является то, что некоторые из них связаны друг с другом определенными соотношениями. Например, точка пересечения медиан М, точка пересечения высот Н и центр описанной окружностиР лежат на одной

прямой,названной позже прямой Эйлера.

Окружность девяти точек

В 1765 году Эйлер обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности. Впоследствии было обнаружено, что на той же окружности лежат ещё триточки — середины отрезков , соединяющих ортоцентр с вершинами треугольника. Это и есть окружность девяти точек.

Пусть дан ∆АВС. Точкой Торричелли данного треугольника называется такая точка М внутри этого треугольника, из которой стороны данного треугольника видны под углом 120 ⁰ , т. е. углы АМВ, АМС и ВМС равны 120 ⁰ . (Замечание: точка Торричелли существует, если все углы треугольника меньше 120 ⁰ .)

Точками Брокара ∆АВС называются такие его внутренние точки Р и Q, что

Примеры решения задач

Задача 1. В остроугольном ∆АВС проведена медиана ВМ, биссектриса АК и высота АН (Н лежит между К и В) так, что МК=КН=НВ. Найти отношение сторон ∆АВС.

Решение. Пусть МК=КН=НВ=х, тогда МС=3х. По свойству биссектрисы = = = . Так как АН высота, то в прямоугольных треугольниках АНВ и АНС по теореме Пифагора следует, что АН 2 =АВ 2 -ВН 2 =АС 2 -НС 2 или АВ 2 -х 2 =4АВ 2 -25х 2 , отсюда х= АВ. Получаем, что ВС=6х= АВ. Следовательно, АВ:АС:ВС=1:2:

Ответ: АВ:АС:ВС=1:2: .

Задача 2. Серединный перпендикуляр к стороне АС ∆АВС пересекает сторону ВС в точке D. Найти ВD и DС, если АD=5 см, ВС=9см.

Решение. Пусть КD серединный перпендикуляр к стороне АС. В ∆АDС КD-высота и медиана, а значит он равнобедренный. Следовательно, АD=DС=5см, тогда ВD=ВС-DС=4см

Ответ: ВD=4см, DС=5см

Связь геометрии с природой

Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Я хочу остановиться на примере точки Торричелли, практическом применении этой точки.

В этом положении (положении равновесия) потенциальная энергия рассматриваемой системы имеет наименьшее значение и сумма отрезков МА+МВ+МС будет наименьшей, а сумма векторов, лежащих на этих отрезках с началом в точке Торричелли, равна нулю.

Выводы. В результате выполнения работы мои знания по математике расширились. Я узнала, что кроме известных мне замечательных точек пересечения высот, медиан, биссектрис и серединных перпендикуляров к сторонам треугольника существуют еще замечательные точки и линии треугольника. Полученные знания можно использовать в своей учебной деятельности, применять изученную теорию к решению определенных задач и в реальной ситуации. Считаю, что применение замечательных точек и линий треугольника в изучении математики является эффективным. Знание их значительно ускоряет решение многих задач.

Гипотеза подтвердилась: замечательными точки и линии треугольника взаимосвязаны некоторыми соотношениями.

И. Л. Никольская Факультативный курс по математике, Москва «Просвещение»1991 год