Условие задачи
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка , причём — образующая цилиндра, а AC — диаметр основания. Известно, что
а)Докажите, что угол между прямыми и равен .
б)Найдите объём цилиндра.
Решение
Прямые и параллельны, (как линии пересечения двух параллельных оснований цилиндра третьей плоскостью)
Значит, угол между и равен углу .
(опирается на диаметр).
Для выполняется равенство
6+6=12. Значит, — прямоугольный равнобедренный, .
Видео:Ященко. ЕГЭ. Профильная математика. 27 вариант. 2021. 14 задание. GeoGebra.Скачать

Задание 14. ЕГЭ. В цилиндре образующая перпендикулярна плоскости основания.
Задание. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания – точка С1, причем СС1 – образующая цилиндра, а АС – диаметр основания. Известно, что ∠АСВ = 45 0 , AB = 3√2, CC1 = 6.
а) Докажите, что угол между прямыми AС1 и BС равен 60 0 .
б) Найдите расстояние от точки В до прямой АС1.
Решение:
а) Докажите, что угол между прямыми АС1 и ВС равен 60 0 .
Проведем образующую ВВ1, тогда ВВ1С1С – прямоугольник и ВС параллельна В1С1, поэтому угол между прямыми АС1 и ВС равен углу между прямыми АС1 и В1С1, т. е. равен углу ∠АС1В1.
Угол ∠АВС – вписанный в окружность угол, который опирается на диаметр основания цилиндра, следовательно, ∠АВС = 90 0 и треугольник ΔАВС – прямоугольный треугольник.
Так как ВС ⊥ АВ и ВС ⊥ ВВ1, тогда ВС ⊥ (АВВ1).
т. е. треугольник ΔАВ1С1 – прямоугольный треугольник (∠АВ1С1 = 90 0 ).
Так как угол ∠АСВ = 45 0 , то треугольник ΔАВС – прямоугольный равнобедренный треугольник,
т. е. АВ = ВС = В1С1 = 3√2.
Так как ВВ1 ⊥ (АВС), то треугольник ΔАВВ1 – прямоугольный треугольник,
по теореме Пифагора найдем В1С1:
Подставим значения АВ1 и В1С1 в формулу (1), получим
б) Найдите расстояние от точки В до прямой АС1.
Расстоянием от точки до прямой называется перпендикуляр, проведенный из этой точки к данной прямой.
Прямая АВ ⊥ ВС и АВ ⊥ ВВ1, тогда АВ ⊥ (ВВ1С1) и АВ ⊥ ВС1, т. е. треугольник ΔАВС1 – прямоугольный треугольник (∠АВС1 = 90 0 ).
Тогда расстоянием от точки В до прямой АС1 является высота треугольника ΔАВС1, проведенная из вершины прямого угла к гипотенузе АС1, т. е. ВК.
Площадь треугольника ΔАВС1 равна:
Площадь треугольника ΔАВС1 можно найти другим способом:
Приравняем правые части этих формул:
AB = 3√2
Из прямоугольного ΔВB1С1 по теореме Пифагора найдем ВС1:
ВС1 = 3√6
Из прямоугольного ΔAВС1 по теореме Пифагора найдем AС1:
AС1 = 6√2
Подставим значения АВ, ВС1 и АС1 в формулу (2), получим
Видео:✓ Задача про цилиндр | ЕГЭ-2018. Задание 13. Математика. Профильный уровень | Борис ТрушинСкачать

Решение №1913 В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В …
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания – точки В1 и С1, причем ВВ1 – образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите угол между прямыми ВВ1 и АС1, если АВ = 6, ВВ1 = 15, В1С1 = 8.
🔍 Видео
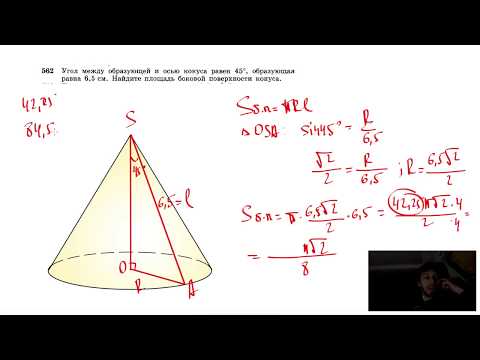
№562. Угол между образующей и осью конуса равен 45°, образующая равна 6,5 см. НайдитеСкачать
10 вариант ЕГЭ Ященко 2024 математика профильный уровеньСкачать

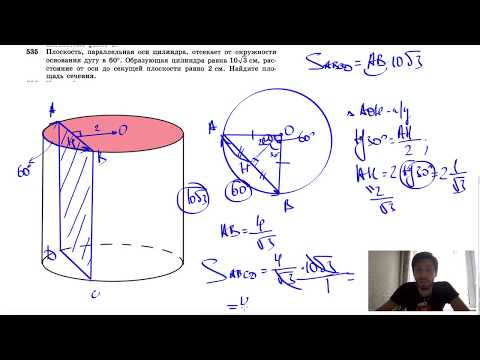
№535. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 60Скачать
Конус. 11 класс.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

№548. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом α. НайдитеСкачать

Решение задач на конусСкачать

Вариант ФИПИ на 100 баллов #27 (математика ЕГЭ профиль)Скачать

Задание 5. ЕГЭ профиль. КОНУС.Скачать

Геометрия 11 класс (Урок№6 - Тела вращения. Цилиндр.)Скачать

Задача 14, вариант 7, Ященко-2019, 36 вариантов, стереометрияСкачать

Математика ЕГЭ-2024. Вариант 9 из сборника И.В. Ященко "36 вариантов заданий". Профильный уровень.Скачать

усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

ВАРИАНТ #27 ЕГЭ 2021 ФИПИ НА 100 БАЛЛОВ (МАТЕМАТИКА ПРОФИЛЬ)Скачать

Вариант ФИПИ на 100 баллов #22 (математика ЕГЭ профиль)Скачать

ЕГЭ 2020 Ященко 17 вариант ФИПИ школе полный разбор!Скачать

На окружности с центром O отмечены точки A и B так ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Урок 19. Задачи на тела вращения из ЕГЭ. Цилиндр, конус, сфера. Стереометрия с нуля.Скачать









