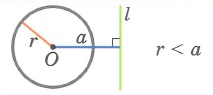
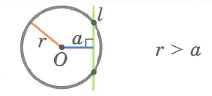
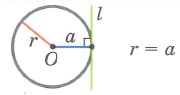
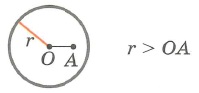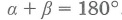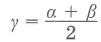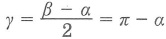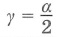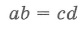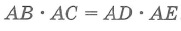- Существует 3 варианта взаимного расположения точки и окружности:
- Как отличить друг от друга эти варианты?
- А как найти расстояние между двумя точками?
- Формула
- Если лень читать
- Взаимное расположение окружности и точки
- Взаимное расположение точки и окружности
- Существует 3 варианта взаимного расположения точки и окружности:
- Как отличить друг от друга эти варианты?
- А как найти расстояние между двумя точками?
- Формула
- Если лень читать
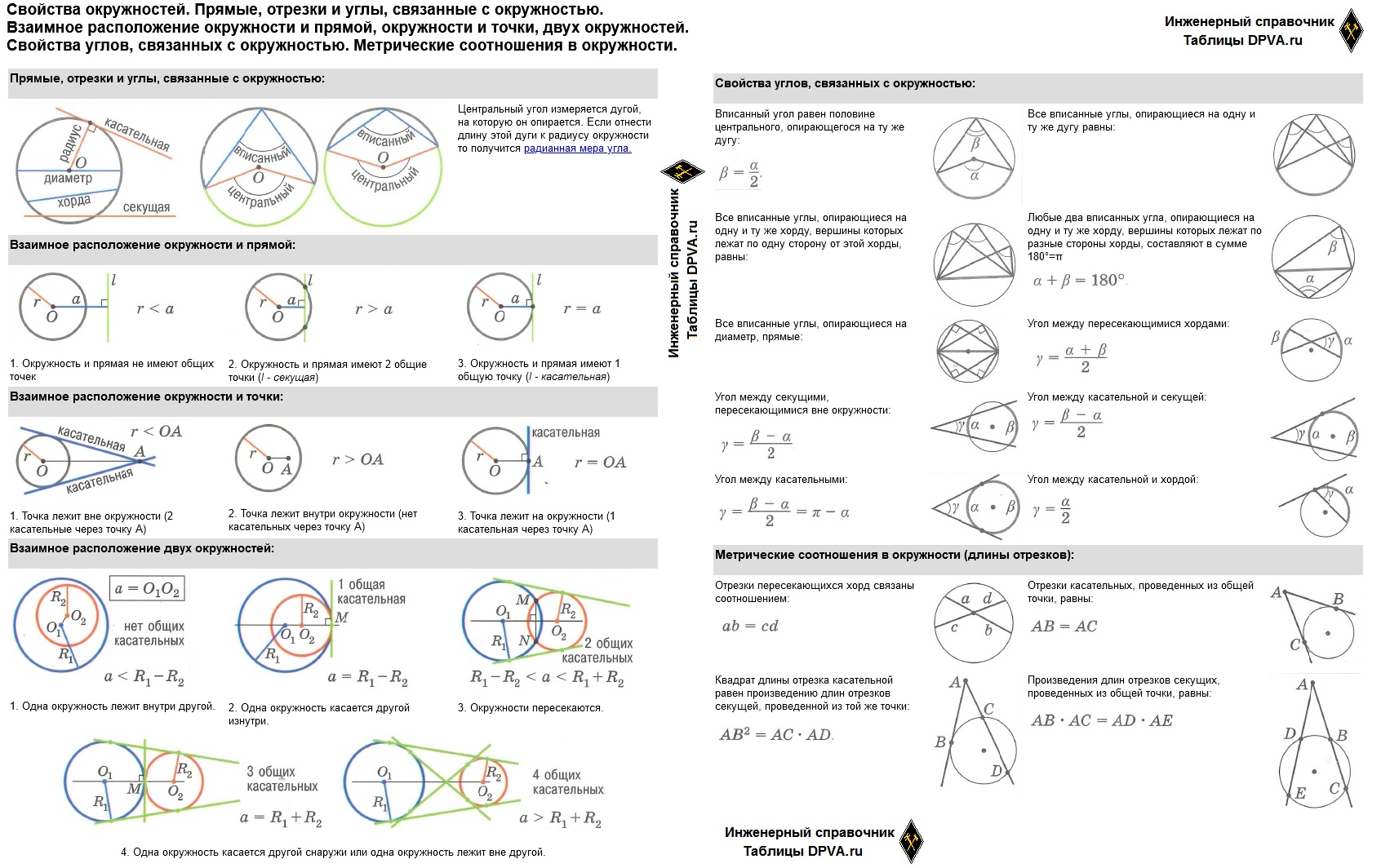
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
- Прямые, отрезки и углы, связанные с окружностью:
- Взаимное расположение окружности и прямой:
- Взаимное расположение окружности и точки:
- Взаимное расположение двух окружностей:
- Свойства углов, связанных с окружностью:
- Метрические соотношения в окружности (длины отрезков):
- Окружность и круг
- Определение окружности и круга
- Пример:
- Центральные углы и дуги окружности
- Вписанные углы
- Пример:
- Взаимное расположение прямой и окружности
- Пример:
- Взаимное расположение двух окружностей
- Пример:
- Окружности, описанные около треугольника и вписанные в треугольник
- Пример:
- Многоугольники, вписанные в окружности и описанные около них
- Вписанные и описанные правильные многоугольники
- Пример:
- Длина окружности
- Пример 1.
- Пример 2.
- Площадь круга
- Части окружности и круга
- Пример 1.
- Пример 2.
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
- Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
- Прямые, отрезки и углы, связанные с окружностью:
- Взаимное расположение окружности и прямой:
- Взаимное расположение окружности и точки:
- Взаимное расположение двух окружностей:
- Свойства углов, связанных с окружностью:
- Метрические соотношения в окружности (длины отрезков):
- 🌟 Видео
Видео:Взаимное расположение окружностей. 7 класс.Скачать

Существует 3 варианта взаимного расположения точки и окружности:
Точка находится внутри круга, ограниченного окружностью:
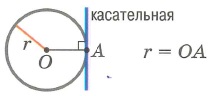
Точка находится на окружности:
Точка находится вне круга, ограниченного окружностью:
Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Как отличить друг от друга эти варианты?
Вспомним определения окружности и круга:
Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга.
Из определений следует, что точка принадлежит окружности тогда и только тогда, когда расстояние между ней и центром равно радиусу, открытому кругу (так называют круг, в который не входит его граница) — когда расстояние меньше радиуса, лежит вне круга — когда расстояние больше радиуса. Картинка ниже подтвеждает это.
Итак, определение положения точки относительно окружности сводится к вычислению расстояния между двумя точками (данной точкой и центром окружности) и сравнению этой величины с радиусом.
Видео:8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

А как найти расстояние между двумя точками?
Точно так же, как длину отрезка или вектора с началом в одной из этих точек и концом в другой, — через теорему Пифагора.
Пусть координаты первой точки, А — (x_1) и (y_1), а второй, B — (x_2) и (y_2):
Построим прямоугольный треугольник с катетами, параллельными осям координат, и гипотенузой AB:
Катет OB в нём равен (x_2-x_1), катет OA — (y_1-y_2), значит, гипотенуза AB – корню из их суммы, т. е. [sqrt] Приведённая выше формула подходит для любых координат точек. Часто значения в скобках получаются отрицательными, в том числе и для катета OA в примере, но при возведении в квадрат знак теряется.
Ещё одна оговорка: при извлечении квадратного корня получается приближённое значение, которое может отличаться от привычного нам. Поэтому, если нам требуется сравнить расстояние с каким-то числом (что мы и собираемся сделать), удобнее не извлекать корень и сравнивать квадрат расстояния с квадратом числа.
Кстати, если вектор задан одной точкой, его длину можно определить по той же формуле, но чуть проще.
В самом деле, здесь (x_1=y_1=0), поэтому формула выглядит как [sqrt] Также ей можно пользоваться, когда одна из точек или один из концов отрезка находится в точке (0;0). Разумеется, здесь тоже действуют оговорки, описанные выше.
Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Формула
Теперь нетрудно вывести формулу, по которой можно определить взаимное расположение точки и окружности.
Если (px) и (py) — координаты точки, (ox) и (oy) — координаты центра окружности, (r) — радиус окружности, то
при ((ox-px)^2+(oy-py)^2lt) точка лежит внутри круга;
при ((ox-px)^2+(oy-py)^2=) точка лежит на окружности;
при ((ox-px)^2+(oy-py)^2gt) точка лежит вне круга.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Если лень читать
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Взаимное расположение окружности и точки
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Взаимное расположение точки и окружности
Видео:Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Существует 3 варианта взаимного расположения точки и окружности:
Точка находится внутри круга, ограниченного окружностью:
Точка находится на окружности:
Точка находится вне круга, ограниченного окружностью:
Видео:Взаимное расположение точки и окружностиСкачать

Как отличить друг от друга эти варианты?
Вспомним определения окружности и круга:
Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга.
Из определений следует, что точка принадлежит окружности тогда и только тогда, когда расстояние между ней и центром равно радиусу, открытому кругу (так называют круг, в который не входит его граница) — когда расстояние меньше радиуса, лежит вне круга — когда расстояние больше радиуса. Картинка ниже подтвеждает это.
Итак, определение положения точки относительно окружности сводится к вычислению расстояния между двумя точками (данной точкой и центром окружности) и сравнению этой величины с радиусом.
Видео:Взаимное расположение и точки пересечения прямой и окружностиСкачать

А как найти расстояние между двумя точками?
Точно так же, как длину отрезка или вектора с началом в одной из этих точек и концом в другой, — через теорему Пифагора.
Пусть координаты первой точки, А — (x_1) и (y_1), а второй, B — (x_2) и (y_2):
Построим прямоугольный треугольник с катетами, параллельными осям координат, и гипотенузой AB:
Катет OB в нём равен (x_2-x_1), катет OA — (y_1-y_2), значит, гипотенуза AB – корню из их суммы, т. е. [sqrt ] Приведённая выше формула подходит для любых координат точек. Часто значения в скобках получаются отрицательными, в том числе и для катета OA в примере, но при возведении в квадрат знак теряется.
Ещё одна оговорка: при извлечении квадратного корня получается приближённое значение, которое может отличаться от привычного нам. Поэтому, если нам требуется сравнить расстояние с каким-то числом (что мы и собираемся сделать), удобнее не извлекать корень и сравнивать квадрат расстояния с квадратом числа.
Кстати, если вектор задан одной точкой, его длину можно определить по той же формуле, но чуть проще.
В самом деле, здесь (x_1=y_1=0), поэтому формула выглядит как [sqrt ] Также ей можно пользоваться, когда одна из точек или один из концов отрезка находится в точке (0;0). Разумеется, здесь тоже действуют оговорки, описанные выше.
Видео:Взаимное расположение окружностей. Точки пересечения окружностейСкачать

Формула
Теперь нетрудно вывести формулу, по которой можно определить взаимное расположение точки и окружности.
Если (px) и (py) — координаты точки, (ox) и (oy) — координаты центра окружности, (r) — радиус окружности, то
при ((ox-px)^2+(oy-py)^2lt ) точка лежит внутри круга;
при ((ox-px)^2+(oy-py)^2= ) точка лежит на окружности;
при ((ox-px)^2+(oy-py)^2gt ) точка лежит вне круга.
Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Если лень читать
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
Видео:70. Взаимное расположение прямой и окружностиСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
Прямые, отрезки и углы, связанные с окружностью:

Взаимное расположение окружности и прямой:
1. Окружность и прямая не имеют общих точек
2. Окружность и прямая имеют 2 общие точки (l — секущая)
3. Окружность и прямая имеют 1 общую точку (l — касательная)
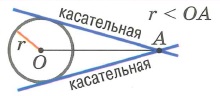
Взаимное расположение окружности и точки:
1. Точка лежит вне окружности (2 касательные через точку А)
2. Точка лежит внутри окружности (нет касательных через точку А)
3. Точка лежит на окружности (1 касательная через точку А)
Взаимное расположение двух окружностей:
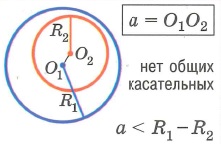
1. Одна окружность лежит внутри другой.
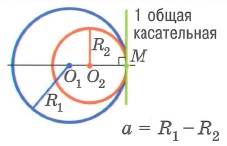
2. Одна окружность касается другой изнутри.
3. Окружности пересекаются.
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.
Свойства углов, связанных с окружностью:
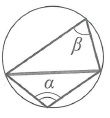
Вписанный угол равен половине центрального, опирающегося на ту же дугу:

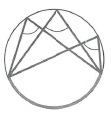
Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π
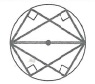
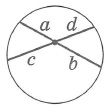
Угол между пересекающимися хордами:
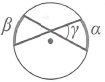
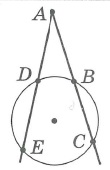
Угол между секущими, пересекающимися вне окружности:
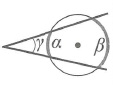
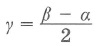
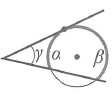
Угол между касательными:
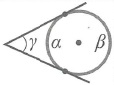
Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):
Отрезки пересекающихся хорд связаны соотношением:
Отрезки касательных, проведенных из общей точки, равны:
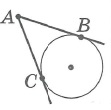
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:
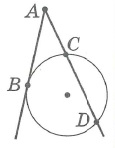
Произведения длин отрезков секущих, проведенных из общей точки, равны:
Консультации и техническая
поддержка сайта: Zavarka Team
Видео:Как искать точки на тригонометрической окружности.Скачать

Окружность и круг
Окружность — это замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки: эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка.
Круг — это часть плоскости, лежащая внутри окружности. Другими словами, это геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа. Число. называется радиусом этого круга.
Содержание:
Определение окружности и круга
Определение. Окружностью называется фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки.
Эта точка называется центром окружности. Расстояние от точек окружности до ее центра называют радиусом окружности. Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром.
Определение. Отрезок, соединяющий две точки окружности, называют хордой. Хорду, проходящую через центр, называют диаметром.
На рисунке 2.151 изображена окружность с центром в точке О. Отрезок OA — радиус этой окружности, BD — хорда окружности, СМ — диаметр окружности.
Определение. Кругом называют фигуру, которая состоит из всех точек плоскости, находящихся на расстоянии, не большем данного от данной точки.
Эту точку называют центром круга, а данное расстояние — радиусом круга. Границей круга является окружность с тем же центром и радиусом (рис. 2.152).
Пример:
На какое наибольшее число различных частей, не имеющих общих точек, кроме своих границ, могут разбивать плоскость: а) две окружности; б) три окружности?
Решение:
Изобразим на рисунке соответствующие условию случаи взаимного расположения фигур. Запишем ответ: а) четыре части (рис. 2.153); б) восемь частей (рис. 2.154).
Центральные углы и дуги окружности
Пусть вершина некоторого угла совпадает с центром окружности (рис. 2.155). Угол АОВ мы будем называть центральным углом.
Определение. Центральным углом в окружности называется плоский угол с вершиной в ее центре.
Часть окружности, расположенная внутри угла, называется дугой окружности, соответствующей этому центральному углу.
Определение. Пересечение окружности и ее центрального угла называют дугой окружности.
Градусной мерой дуги окружности называют градусную меру соответствующего центрального угла.
Градусная мера дуги АВ на рисунке 2.155 равна градусной мере угла АОВ. Градусная мера дуги АВ обозначается 
Можно ввести еще одну важную единицу измерения дуг. При измерении угловой величины дуги окружности за единицу измерения принимается угловая величина дуги этой окружности, длина которой равна радиусу окружности. Эту единицу измерения угловых величин дуг называют радианом.
Сформулируем некоторые свойства измерения дуг окружностей:
— градусная мера дуги не зависит от размера окружности;
— соответствующие дуги двух концентрических окружностей на рисунке 2.156 имеют одну и ту же градусную меру (величину).
— если дуга (на данной окружности) становится больше, то увеличивается и ее величина.
Окружности (или круги) равны, если равны их радиусы. Можно говорить и о равных дугах окружностей, но равные дуги могут быть или у одной окружности или у равных окружностей.
Определение. Две дуги одной и той же окружности или же равных окружностей называют равными, если они имеют одну и ту же градусную меру.
Вписанные углы
Вершина угла может принадлежать окружности. В этом случае мы получаем вписанные углы.
Определение. Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называют вписанным в окружность.
На рисунке 2.157 угол ABC вписанный. Его вершина В принадлежит окружности, стороны ВА и ВС пересекают окружность. В этом случае говорят, что вписанный угол ABC опирается на дугу АС окружности.
Величина вписанного угла выражается в тех же единицах, что и у других углов, а вот правило нахождения этой величины другое.
Теорема 40. Величина вписанного угла равна половине угловой величины дуги, на которую он опирается.
При доказательстве теоремы 40 необходимо рассмотреть три разных случая, которые изображены на рисунках 2.158—2.160: одна из сторон вписанного угла проходит через центр окружности (рис. 2.158); центр окружности лежит внутри вписанного угла (рис. 2.159); центр окружности лежит внутри вписанного угла (рис. 2.160).
Из теоремы 40 можно получить следующие следствия:
Следствие 1. Все вписанные в окружность углы, стороны которых проходят через две данные точки окружности, а вершины лежат по одну сторону от прямой, соединяющей эти точки, равны.
Следствие 2. Вписанные углы, стороны которых проходят через концы диаметра окружности, прямые.
На рисунке 2.161 стороны вписанного угла ABC проходят через концы диаметра АС, поэтому
Пример:
Точки А, В и С лежат на окружности с центром О. Найдите угол АОС, если
Решение:
Из условия задачи имеем:
1. Точки А, В и С лежат i
2.
3. Найдите
4. Угол ABC, вписанный в окружность, опирается на дугу АС (1, определение вписанного угла).
5. 

6. 
Взаимное расположение прямой и окружности
Возможны три случая взаимного расположения прямой и окружности, если эта прямая и окружность лежат в одной плоскости:
а) прямая имеет две общие точки с окружностью;
б) прямая имеет только одну общую точку с окружностью;
в) прямая не имеет общих точек с окружностью.
Перечислим условия, определяющие все возможные случаи взаимного расположения прямой и окружности, в зависимости от расстояния между центром окружности и прямой.
1) Если расстояние от центра окружности до прямой больше радиуса, то прямая и окружность не имеют общих точек (рис. 2.163). При этом окружность лежит по одну сторону от прямой.
2) Если расстояние от центра окружности до прямой равно радиусу, то окружность имеет с прямой единственную общую точку, т. е. прямая касается окружности (рис. 2.164). И в этом случае окружность лежит по одну сторону от прямой.
3) Если расстояние от центра окружности до прямой меньше радиуса, то прямая пересекает окружность ровно в двух точках (рис. 2.165). В этом случае прямая разбивает окружность на две части.
Определение. Если прямая имеет две общие точки с окружностью, то говорят, что прямая и окружность пересекаются. В этом случае прямая называется секущей.
Можно доказать свойство секущей окружности.
Теорема 41. Если прямая проходит через точку, внутреннюю относительно окружности, то она является секущей, т. е. пересекает окружность в двух точках.
Определение. Прямую, имеющую с окружностью только одну общую точку, называют касательной к окружности, а общую точку прямой и окружности — точкой касания (рис. 2.166).
Все точки касательной, кроме точки касания, лежат вне данной окружности. Действительно, если предположить, что на касательной АВ имеется хотя бы одна точка, лежащая внутри окружности, то прямая АВ должна пересекать окружность в двух точках, поэтому она не может быть касательной.
Прямая и окружность могут иметь только одну общую точку, но через эту точку может проходить бесконечное множество прямых, не лежащих с окружностью в одной плоскости (рис. 2.167).
Теорема 42. Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.
Теорема 43. Если прямая перпендикулярна радиусу окружности и проходит через его конец, лежащий на окружности, то она является касательной к этой окружности.
Пример:
Постройте касательную к данной окружности с центром О и радиусом 
Решение:
Из условия задачи имеем: (рис. 2.168)
1. Окр. (О, 
2. Точка А на окружности.
3. Требуется построить касательную к окружности, проходящую через точку А.
Анализ. Предположим, что задача решена и построена касательная АВ к окружности (рис. 2.168). По теореме 42 касательная АВ перпендикулярна радиусу OA в точке А, поэтому, если построить прямую АВ, перпендикулярную OA, то эта прямая будет искомой.
Построение. Нужно построить перпендикуляр АВ к прямой OA в точке А. Это построение можно свести к построению серединного перпендикуляра к отрезку 
Задача имеет только одно решение. Действительно, касательная, проходящая через точку А, должна быть перпендикулярна прямой OA (т. 42), а через точку А в плоскости данного радиуса проходит только одна прямая АВ, перпендикулярная к прямой OA (т. 41).
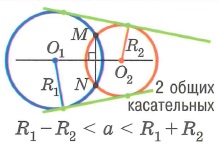
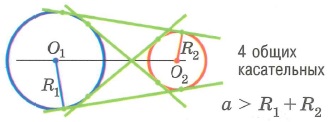
Взаимное расположение двух окружностей
На рисунке 2.169 изображены две окружности с радиусом 







Представьте теперь, что первая окружность передвигается так, что расстояние h между центрами 



При дальнейшем уменьшении расстояния h окружности будут пересекаться, то есть иметь две общие точки (рис. 2.171). При этом
В случае, когда 
При дальнейшем уменьшении расстояния между центрами, т. е. при условии 
Итак, в зависимости от соотношений между h, 
а) 
б) 
B) 
г) 
д) 
е) h = 0 — окружности являются концентрическими.
Пример:
Две окружности диаметром 4 и 8 см касаются внешним образом. Чему равно расстояние между центрами окружностей?
Решение:
Радиусы окружностей 
Окружности, описанные около треугольника и вписанные в треугольник
Определение. Окружность называют описанной около треугольника, если она проходит через все его вершины.
На рисунке 2.176 изображен треугольник ABC, вписанный в окружность, а окружность будет описана около этого треугольника.
Теорема 44. Около любого треугольника можно описать окружность и притом только одну. Центр такой окружности — точка пересечения серединных перпендикуляров к сторонам треугольника (рис. 2.176).
Определение. Окружность называют вписанной в треугольник, если она касается всех его сторон.
Теорема 45. Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис. 2.177).
Пример:
В прямоугольном треугольнике катеты равны 12 и 16 см. Вычислите радиусы: 1) вписанной в него окружности; 2) описанной окружности.
Решение:
1) Из условия задачи имеем:
1. Треугольник ABC, в котором 
2. О — центр вписанной окружности.
3. Найдите радиус вписанной окружности.
4. ОМ = OL = ОК = 



Надо найти 
5. АО, ВО, СО — биссектрисы углов 
6. 
7. MA = КА, KB = LB (6).
8. 
Вычислим два раза периметр 
9. АВ + ВС + СА = 2АВ + 
10. 

2) Центр описанной около прямоугольного треугольника окружности совпадает с серединой гипотенузы, откуда радиус описанной окружности R = 10 см (рис. 2.180).
Многоугольники, вписанные в окружности и описанные около них
Определение. Многоугольник называют вписанным в окружность, если все его вершины лежат на этой окружности.
На рисунке 2.181 изображен пятиугольник, вписанный в окружность, его вершины А, В, С, D, Е лежат на окружности с центром в точке О, а значит, OA = OB = ОС = OD = ОЕ = 

Определение. Многоугольник называется описанным около окружности, если все его стороны касаются этой окружности.
На рисунке 2.182 шестиугольник ABCDEF описан около окружности.
Не всякий многоугольник можно вписать в окружность и не около всякого многоугольника можно описать окружность.
Далее сформулированы свойства и признаки вписанных в окружность четырехугольников.
Например, есть четырехугольники, которые можно вписать в окружность (квадрат всегда можно вписать в окружность, рис. 2.183). А вот ромб вписать в окружность (рис. 2.184) нельзя.
Теорема 46. Сумма противоположных углов вписанного в окружность четырехугольника равна 
Теорема 47. Если четырехугольник описан около окружности, то суммы длин его противолежащих сторон равны.
Теорема 48. Если сумма двух противоположных углов четырехугольника равна 
Теорема 49. Если суммы длин противолежащих сторон четырехугольника равны, то в него можно вписать окружность.
Вписанные и описанные правильные многоугольники
Теорема 50. Около всякого правильного многоугольника можно описать окружность.
Теорема 51. Во всякий правильный многоугольник можно вписать окружность.
Теорема 52. Правильный выпуклый многоугольник является вписанным в окружность и описанным около окружности.
Радиус R окружности, описанной около правильного 

Радиус окружности, вписанной в правильный 

Сторону правильного 

Теорема 53. Сторона 

Из этой теоремы можно получить следующие следствия.
Следствие 1.
Действительно,
Следствие 2.
Следствие 3.
Пример:
Впишите в данную окружность правильный восьмиугольник.
Решение:
Два перпендикулярных диаметра делят окружность на четыре равные части. Для построения правильного восьмиугольника необходимо каждую из этих частей разделить пополам, т. е. провести биссектрисы прямых углов, и полученные восемь точек окружности последовательно соединить отрезками. Получим вписанный в окружность восьмиугольник (рис. 2.185). Равенство сторон и равенство углов восьмиугольника следует из равенства всех восьми треугольников, которые равны по двум сторонам и углу между ними. Следовательно, полученный восьмиугольник правильный.
Длина окружности
Из наглядных соображений ясно, что длина окружности сколь угодно мало отличается от периметра вписанного в нее многоугольника с достаточно малыми сторонами. Имеет место такое свойство длины окружности.
Теорема 54. Отношение длины окружности к ее диаметру не зависит от окружности, т. е. одно и то же для любых двух окружностей.
Отношение длины окружности к диаметру обозначают греческой буквой 



Таким образом, длина окружности вычисляется по формуле
На рисунке 2.186 изображена дуга АВ окружности с центром О.
Длина дуги окружности, соответствующей центральному углу в 
Радианной мерой угла называют отношение длины соответствующей дуги к радиусу окружности. Из формулы длины дуги окружности следует, что 



Единицей радианной меры углов является радиан. Угол в один радиан — это центральный угол, у которого длина дуги равна радиусу. Градусная мера угла в один радиан равна
Пример 1.
Точки М и N делят окружность на две дуги, разность градусных мер которых равна 90°. Чему равны градусные меры каждой из дуг?
Решение:
Сумма градусных мер дуг равна 360°, а разность равна 90°. Обозначим градусные меры этих дуг х и у. Имеем:
Решая эту систему, получим х = 225°, у = 135°.
Пример 2.
Сторона квадрата равна 4 см. Вычислите длину окружности: 1) вписанной в него; 2) описанной около него.
Решение:
1) Радиус вписанной в квадрат окружности равен 2 см, тогда длина окружности равна
2) Радиус окружности, описанной около квадрата, равен 

Площадь круга
Коэффициент подобия двух кругов равен отношению их диаметров или радиусов. Отношение площадей двух подобных фигур равно квадрату их коэффициента подобия. Следовательно, площади двух кругов относятся как квадраты их радиусов. Обозначим радиус круга через S. Отношение площадей 

Итак, площади кругов пропорциональны квадратам их радиусов.
Коэффициент их пропорциональности, как и в случае с длиной окружности, равен числу 
Площадь круга выражается формулой:
Через диаметр площадь круга выражается формулой:
Части окружности и круга
Определение. Круговым сектором называют часть круга, лежащую внутри соответствующего центрального угла (рис. 2.186).
Площадь кругового сектора вычисляется по формуле
где 

Определение. Круговым сегментом называют общую часть круга и полуплоскости, граница которой содержит хорду этого круга (рис. 2.187, 2.188).
Площадь кругового сегмента, не равного полукругу, вычисляется по формуле
где 




Пример 1.
Проведите необходимые измерения и вычислите площади фигур, изображенных на рисунках 2.189—2.191.
Решение:
а) 
где 

Например, при
б) Считая, что АОВ — сектор с углом 120°, О — центр окружности (рис. 2.190), получим:
где 
в) Считая, что дуга АОС (рис. 2.191) проходит через центр окружности О, а ее радиус равен радиусу окружности и 
где 
Например, при
Пример 2.
Докажите, что сумма площадей двух заштрихованных луночек (рис. 2.192) равна площади прямоугольного треугольника ABC.
Решение:
Обозначим катеты прямоугольного треугольника ABC через 
По теореме Пифагора 
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Урок по геометрии ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности.
Прямые, отрезки и углы, связанные с окружностью:

Взаимное расположение окружности и прямой:
1. Окружность и прямая не имеют общих точек
2. Окружность и прямая имеют 2 общие точки (l — секущая)
3. Окружность и прямая имеют 1 общую точку (l — касательная)
Взаимное расположение окружности и точки:
1. Точка лежит вне окружности (2 касательные через точку А)
2. Точка лежит внутри окружности (нет касательных через точку А)
3. Точка лежит на окружности (1 касательная через точку А)
Взаимное расположение двух окружностей:
1. Одна окружность лежит внутри другой.
2. Одна окружность касается другой изнутри.
3. Окружности пересекаются.
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой.
Свойства углов, связанных с окружностью:
Вписанный угол равен половине центрального, опирающегося на ту же дугу:



Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π


Угол между пересекающимися хордами:

Угол между секущими, пересекающимися вне окружности:

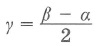

Угол между касательными:

Угол между касательной и хордой:

Метрические соотношения в окружности (длины отрезков):
Отрезки пересекающихся хорд связаны соотношением:

Отрезки касательных, проведенных из общей точки, равны:

Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:

Произведения длин отрезков секущих, проведенных из общей точки, равны:


Консультации и техническая
поддержка сайта: Zavarka Team
🌟 Видео
Длина окружности. Площадь круга. 6 класс.Скачать

Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Окружность и прямая: варианты взаимного расположенияСкачать