В равнобедренной трапеции авсд через вершину б проведена прямая которая параллельна стороне сд

Геометрия | 5 — 9 классы

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N.

Периметр треугольника ABN равен 27 см, CB равно 6 см.

Вычисли периметр трапеции ABCD.

Видео:Геометрия В трапеции ABCD меньшее основание BC равно 6 см. Через вершину B проведена прямая, котораяСкачать

В прямоугольнике ABCD через точку P проведены прямая KM, параллельная сторонам AD и BC, и прямая LN, параллельная сторонам AB и CD?

В прямоугольнике ABCD через точку P проведены прямая KM, параллельная сторонам AD и BC, и прямая LN, параллельная сторонам AB и CD.

Периметр прямоугольника KBLP равен 8 см, а периметр прямоугольника NPMD равен 18 см.

Найдите периметр прямоугольника ABCD.

Видео:Геометрия Через вершину C трапеции ABCD проведена прямая, которая параллельна боковой стороне ABСкачать

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N?

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N.

Периметр треугольника ABN равен 38 см, CB равно 8 см.

Вычисли периметр трапеции ABCD.

Видео:ОГЭ 2022 Математика Задача №23 Вариант 4 Сборник под редакцией Ященко 36 вариантов.Скачать

В трапеции ABCD сторона AD — большее основание?

В трапеции ABCD сторона AD — большее основание.

Через вершину В проведена прямая, параллельная CD, до пересечения AD в точке Е.

Найдите периметр трапеции, если ВС = 6 см, АЕ = 4 см, периметр ABE = 12 см.

С подробнейшим объяснением!

Лучшим ответ будет если он будет с рисунком.

Видео:ОГЭ-2020, математика, Ященко И.В. 36 вариант, задача№ 24.Скачать

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N?

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N.

Периметр треугольника ABN равен 28 см, CB равно 5 см.

Вычисли периметр трапеции ABCD.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В трапеции ABCD AD — большее основание?

В трапеции ABCD AD — большее основание.

Через вершину С проведена прямая, параллельная АВ, до пересечения с АD в точке Е, DE = 6 см, АЕ = 9 см.

Найдите : а) длину средней линии трапеции.

Б) периметр трапеции, если периметр треугольника СDE = 19 см.

Видео:8 класс, 6 урок, ТрапецияСкачать

ПОМОГИТЕ СРОЧНО ?

Через вершину D трапеции ABCD проведена прямая , параллельная боковой стороне AB.

На этой прямой взята точка K.

Найдите площадь трапеции ABCD , если площадь треугольника ABK равна Q , а площадь треугольника ABC = S.

Видео:ОГЭ без рекламы математика задача 25 7 и 8 вариантСкачать

Через вершину M трапеции KMPT проведена прямая, параллельная боковой стороне PT?

Через вершину M трапеции KMPT проведена прямая, параллельная боковой стороне PT.

Она пересекает большее основание KT трапеции в точке E.

Периметр треугольника KME равен 17см, MP = 8 см, KE = 4 см вычислите : а) длину средней линии трапеции б) периметр трапеции.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

В трапеции АВСД меньшее основание ВС равно 4 см?

В трапеции АВСД меньшее основание ВС равно 4 см.

Через вершину В проведена прямая параллельная стороне СД.

Периметр образовавщегося треугольника равен 12 см.

Найдите периметр трапеции.

Видео:№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

Известно, что AD — большее основание трапеции ABCD?

Известно, что AD — большее основание трапеции ABCD.

Через вершину B проведена прямая, которая параллельна стороне CD и пересекает основание AD в точке M.

Найдите периметр трапеции ABCD, если периметр треугольника ABM равен 28 см, а основание BC — 5 см.

Видео:Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N?

В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N.

Периметр треугольника ABN равен 27 см, CB равно 7 см.

Вычисли периметр трапеции ABCD.

На этой странице находится ответ на вопрос В равнобедренной трапеции ABCD через вершину B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Ответ : |Am = √13 ед. |АС| = 5 ед. Объяснение : Вектор Am равен сумме векторов АВ и Вm. Вектор AС равен сумме векторов АВ и ВС. Модуль суммы двух векторов можно вычислить, используя теорему косинусов : |Аm|² = |AB|² + |Bm|² + 2 * |AB| * |Bm| * Co..

4х + х + х = 180 градусов х = 30 градусов углы : 30 30 и 120 медиана = боковая сторона синуса синус а = 30 градусов — а это 0. 5 6 = х * 0. 5 х = 12 ответ : 12см.

Свойство вн. Угла это сумма двух углов ∆ не смежные с ним. Поэтому 47 + 72 = 119.

Угол АОВ = 180 — 100 = 80 градусов(смежные угла) 2) АО = ВО(радиусы равны) 3)треугол. АОВ равнобедренный следовательно, Угол Ова и угол ОАВ = 180 — 80 = 100 : 2 = 50 градусов(по св. Равнобедренных треугольников.

1. BD = AC OB = OC BD = BO + OB AC = OC + AO Тогда AO = OB. Итак, BO = BO, AO = OB, ∠BOA = ∠COA — как вертикальные, значит, ΔAOB = ΔCOD — по I признаку. 2. ∠BOA = 180° — ∠1 — как смежные ∠BOC = 180° — ∠2 — как смежные Но∠1 = ∠2⇒∠BOA = ∠BOC. Итак, ..

Ρ = m / V V = 4 / 3 * π R³ = 4 / 3 * π * 0, 3³≈ 4 / 3 * 3 * 0, 027 = 0, 908(м³) ρ = 118, 75 / 0, 908 ≈ 130, 8кг / м³.

Дано : SАВС — правильная пирамида, ΔАВС — правильный, АВ = ВС = АС = 6 см ; SО — высота пирамиды равна 12 см. Построим ВК⊥АС, ВК — высота, медиана и биссектрисаΔАВС. ОК : ОВ = 1 : 2. ΔВСК. СК = 0, 5·АС = 3 см. ВК² = ВС² — СК² = 36 — 9 = 27, ВК =..

2АК = КС, значит АК : КС = 1 : 2 и АК : АС = 1 : 3. Следствием теоремы о площади треугольника по его стороне и высоте, к ней проведённой, является то, что отношение площадей треугольников с одинаковыми высотами равно отношению их сторон, к которым в..

Поскольку в трапеции основы паралельные, то имеем равнобедренный треугольник с основой диагональю. Получаем что боки равнобокой трапеции равны по 12. Отсуда периметр 12 + 12 + 12 + 18 = 36 + 18 = 54.

Видео:Проверьте себя, задание 2 - Геометрия 8 класс МерзлякСкачать

В равнобедренной трапеции ABCD через верхушку B проведена ровная, которая параллельна

В равнобедренной трапеции ABCD через верхушку B проведена прямая, которая параллельна стороне CD и пересекает сторону AD в точке N.
Периметр треугольника ABN равен 28 см,
CB одинаково 5 см.
Вычисли периметр трапеции ABCD. помогите. даю 25 баллов

• Камилла Хитрикова
• Геометрия 2019-03-09 00:15:58 0 1

BCND — параллелограмм, так как ВСND, BNCD.

Значит CD = BN и ND = BC = 5 см

Pabn = AB + BN + AN = AB + CD + AN = 28 см

Pabcd = AB + BC + CD + AD = AB + 5 + CD + (AN + ND) =
= (AB + CD + AN) + 5 + ND = 28 + 5 + ND = 33 + ND

Видео:№ 201-300 - Геометрия 8 класс МерзлякСкачать

Задача 16 геометрия на ЕГЭ-2021 по математике

На этой странице — обзор разных типов заданий № 16 ЕГЭ-2021 по математике, то есть задач по геометрии.

Все они имеют нечто общее: во-первых, это стандартный уровень сложности, то есть вполне решаемые задачи. Пункт (а) в них вообще простой.

Во-вторых, в каждой из них применяются свойства четырехугольников, вписанных в окружности.

В первой задаче такая окружность находится почти сразу, причем она – вспомогательная, и ее можно даже не изображать на чертеже. Главное – найти равные вписанные углы, опирающиеся на равные дуги или на одну дугу.

Также здесь использована формула синуса тройного угла. Если вы ее забыли – не беда. Ведь а формулу синуса суммы вы знаете.

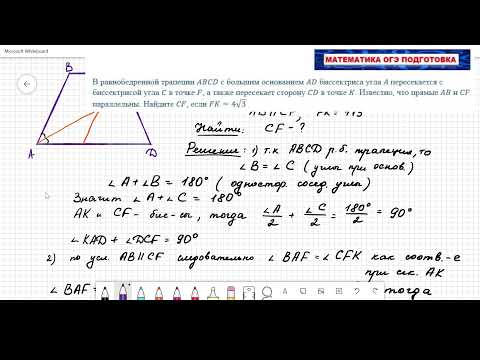
1. Дана равнобедренная трапеция ABCD, в которой меньшее основание ВС равно боковой стороне. Точка Е такова, что ВЕ перпендикулярно AD и СЕ перпендикулярно BD.
а) Доказать, что угол АЕВ равен углу BDA.
б) Найти площадь трапеции ABCD, если АВ = 32, косинус угла АDВ равен

– равнобедренный, CM – высота, проведенная к основанию, значит, M – середина BD.

Докажем, что точки A, B, C, D, E лежат на одной окружности.

ABCD – равнобедренная трапеция, ее можно вписать в окружность.

В – медиана и высота, значит, равнобедренный, BE = ED.

Тогда по трем сторонам, четырехугольник BCDE можно вписать в окружность, т.к.

Так как вокруг можно описать только одну окружность и вокруг четырехугольников ABCD и BCDE тоже можно описать окружность, точки A, B, C, D, E лежат на одной окружности, так как опираются на одну и ту же дугу AB (точки E и D лежат по одну сторону от прямой AD).

б) Так как AB = BC = CD, то дуги AB, BC и CD также равны.

Четырехугольник ABDE вписан в окружность, тогда

По формуле синуса тройного угла,

тогда по теореме синусов

Проведем в трапеции ABCD высоту CK, тогда

BH и CK – высоты трапеции, а так как трапеция равнобедренная, то

Во второй задаче мы увидим ту же идею: вспомогательную окружность. Это один из методов, помогающих решать задачи ЕГЭ по геометрии. Есть здесь и другой мощный прием – использование двух пар подобных треугольников. И еще свойство высоты прямоугольного треугольника, проведенной к гипотенузе. Если вы в восьмом и девятом классе учили геометрию – вы должны владеть этими приемами.

2. Дан прямоугольный треугольник АВС с прямым углом С. Из вершины С на гипотенузу опущена высота СН, на АС и ВС соответственно отмечены точки М и N так, что угол MHN – прямой.
а) Докажите, что треугольники МNH и АВС подобны.
б) Найдите СN, если АС = 5, СМ = 2, ВС = 3.

а) Рассмотрим четырехугольник CMHN.

по условию, значит, CMHN можно вписать в окружность; вписанные, опираются на дугу HN.

Запишем соотношение сходственных сторон.

По условию, AM = 3, найдем CH — высоту

по теореме Пифагора,

AH — проекция катета AC на гипотенузу, по свойствам прямоугольного треугольника, отсюда

В следующей задаче мы снова видим окружность и вписанную в нее трапецию. И наверное, вы уже заметили: пункт (а) задач по геометрии на ЕГЭ часто оказывается подсказкой для решения пункта (б). То, что мы доказали в (а), мы используем в пункте (б).

3. Даны 5 точек на окружности: A, B, C, D, E, причем АЕ = ED = CD, ВЕ перпендикулярен АС.
Точка Т – точка пересечения АС и BD.
а) Докажите, что отрезок ЕС делит отрезок ТD пополам.
б) Найдите площадь треугольника АВТ, если BD = 10, АЕ =

Докажем, что M — середина TD.

Если AE = ED = DC, то дуги AE, ED, DC, также равны;

— накрест лежащие, при пересечении AC и DE секущей CE, значит, AEDC — равнобедренная трапеция. значит, BD — диаметр окружности.

(опирается на диаметр), по катету и гипотенузе, тогда DM — биссектриса равнобедренного т.к. — равнобедренный, то DM — медиана M — середина CE, кроме того, DM — высота

В — медиана и высота, значит, — равнобедренный, а так как — накрест лежащие, при параллельных прямых AC и DE и секущей CE, то по боковой стороне и углу при основании, тогда

CDET — ромб, M — точка пересечения его диагоналей, M — середина TD.

Мы нашли, что AE = ED = CD = CT = ET.

BD = 10 — диаметр окружности.

— равнобедренный, AE = ET, — высота и медиана

Тогда BN — медиана и высота — равнобедренный, AB = BT.

Обозначим тогда — опираются на дугу AE,

Из по теореме синусов:

И еще одна трапеция, вписанная в окружность. Теперь вы точно выучите ее свойства наизусть! Также здесь применяется теорема о пересекающихся хордах. Все эти полезные теоремы, свойства и признаки можно найти в нашей универсальной шпаргалке – Справочнике Анны Малковой для подготовки к ЕГЭ по математике. Скачать Справочник бесплатно можно здесь.

4. Трапеция с большим основанием AD и высотой ВН вписана в окружность. Прямая BH пересекает окружность в точке К.

б) Найдите AD, если: радиус окружности равен шести, СК пересекается с AD в точке N и площадь четырехугольника BHNC в 24 раза больше, чем плошать треугольника KHN.

а) Трапеция ABCD вписана в окружность, следовательно, AB = CD (трапеция равнобокая)

Тогда — вписанные, опираются одну и ту же на дугу AK;

следовательно, CK — диаметр окружности, так как вписанный угол, опирающийся на диаметр, прямой; — опирается на диаметр CK, значит,

(опираются на дугу BC), тогда

Обозначим так как HE = BC,

Из подобия треугольников KNH и KCB следует, что тогда

По теореме о пересекающихся хордах,

Представив левую часть уравнения как разность квадратов, получим:

По смыслу задачи тогда и значит

Задача по геометрии на ЕГЭ по математике оценивается в 3 балла. Как видите, в 2021 году эти 3 балла за геометрию можно было получить без особенных трудностей. На нашем Онлайн-курсе подготовки к ЕГЭ мы решаем и такие задачи по геометрии, и более сложные. Если ты сейчас в 10-м или в 11-м классе – попробуй бесплатно Демо-доступ к Онлайн-курсу.

5. (Резервный день) Окружность с центром О, построенная на катете АС прямоугольного треугольника АВС, как на диаметре, пересекает гипотенузу АВ в точках А и D. Касательная, проведенная к этой окружности в точке D, пересекает катет ВС в точке М.

А) Докажите, что ВМ = СМ
Б) Прямая DM пересекает прямую АС в точке Р, прямая ОМ пересекает прямую ВР в точке К.

Найдите ВК : КР, если

а) Так как – радиус окружности, – равнобедренный, так как (касательная перпендикулярна радиусу, проведенному в точку касания), тогда

– угол между касательной и хордой,

Тогда т.е. – высота – прямоугольный, – равнобедренный, отсюда

Найдем BK : KP, если тогда

Значит, (вертикальные), — равнобедренный, тогда так как MK – биссектриса

📸 Видео

№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

№38. Через вершину А ромба ABCD проведена прямая а, параллельная диагонали BD,Скачать

№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

№384. Через середину М стороны АВ треугольника ABC проведена прямая,Скачать

Трапеция | Задачи 11-24 | Решение задач | Волчкевич |Уроки геометрии в задачах 7-8Скачать

№90. Вершины А и В трапеции ABCD лежат в плоскости α, а вершины С и D не лежат в этой плоскости. КакСкачать

ТРАПЕЦИЯ . §8 геометрия 8 классСкачать

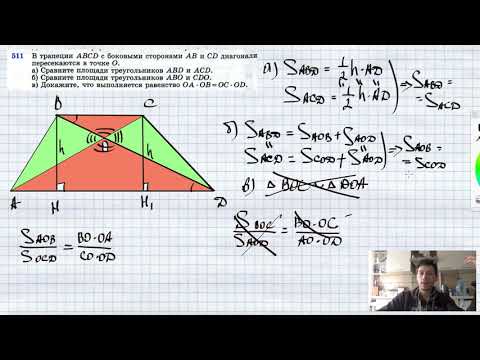
№511. В трапеции ABCD с боковыми сторонами АВ и CD диагонали пересекаются в точке О. а) Сравните плоСкачать