Как обозначить окружность буквами

Окружность — это геометрическая фигура, образованная замкнутой кривой линией, все точки которой одинаково удалены от одной и той же точки.

Точка, от которой одинаково удалены все точки окружности, называется центром окружности. Центр окружности обычно обозначают большой латинской буквой O:

Окружность делит плоскость на две области — внутреннюю и внешнюю. Геометрическая фигура, ограниченная окружностью, — это круг:

Видео:Радиус и диаметрСкачать

Построение окружности циркулем

Для построения окружности используют специальный прибор — циркуль:

Установим циркулю произвольный раствор (расстояние между ножками циркуля) и, поставив его ножку с остриём в какую-нибудь точку плоскости (например, на листе бумаги), станем вращать циркуль вокруг этой точки. Другая его ножка, снабжённая карандашом или грифелем, прикасающимся к плоскости, начертит на плоскости замкнутую линию — окружность:

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Радиус, хорда и диаметр

Радиус — это отрезок, соединяющий любую точку окружности с центром. Радиусом также называется расстояние от точки окружности до её центра:

Все радиусы окружности имеют одну и ту же длину, то есть они равны между собой. Радиус обозначается буквой R или r.

Хорда — это отрезок, соединяющий две точки окружности. Хорда, проходящая через центр, называется диаметром окружности.

Диаметр обозначается буквой D. Диаметр окружности в два раза больше её радиуса:

Дуга — это часть окружности, ограниченная двумя точками. Любые две точки делят окружность на две дуги:

Чтобы различать дуги, на которые две точки разделяют окружность, на каждую из дуг ставят дополнительную точку:

Для обозначения дуг используется символ :

• AFB — дуга с концами в точках A и B, содержащая точку F;
• AJB — дуга с концами в точках A и B, содержащая точку J.

О хорде, которая соединяет концы дуги, говорят, что она стягивает дугу.

Хорда AB стягивает дуги AFB и AJB.

Видео:Математика 3 класс (Урок№33 - Круг. Окружность (центр, радиус, диаметр)Скачать

Как записать окружность в дано

Окружность. Основные понятия и обозначения. Число π.

Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки.

Основные понятия:

Центр окружности – это точка, равноудаленная от точек окружности.

Радиус – это расстояние от точек окружности до ее центра (равен половине диаметра, рис.1).

Диаметр – это хорда, проходящая через центр окружности (рис.1).

Хорда – это отрезок, соединяющий две точки окружности (рис.1).

Касательная – это прямая, имеющая только одну общую точку с окружностью. Проходит через точку окружности перпендикулярно диаметру, проведенному в эту точку (рис.1).
Касательная всегда перпендикулярна диаметру (радиусу), проведенному к точке касания.

Секущая – это прямая, проходящая через две различные точки окружности (рис.1).

Единичная окружность – это окружность, радиус которой равен единице.

Центральный угол – это угол с вершиной в центре окружности. Равен градусной мере дуги, на которую опирается (рис.2).

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Равен половине градусной меры дуги, на которую опирается, либо дополняет половину этого угла до 180° (рис.3).

Вписанный угол, опирающийся на дугу длиной в половину окружности, равен 90°.

Обозначения:

C – длина окружности,

r или R – радиус,

φ – центральный угол,

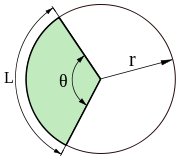
L – длина дуги окружности.

Число π:

Отношение длины окружности к длине ее диаметра обозначается греческой буквой π (пи).

Число π – постоянная величина, которая не меняется в зависимости от величины окружности:

Дуга окружности.

Дуга окружности – это часть окружности, разделенная двумя несовпадающими точками окружности.

Угол, образуемый дугой окружности, равной длине радиуса, есть 1 радиан (рис.4).

1 радиан = 180 0 : π ≈ 57 0 17 ‘ 45 »

1 радиан ≈ 57,3 0

Длину дуги окружности, образованной центральным углом, можно вычислить в радианах по формуле:

L = φR

где R – радиус окружности, φ – центральный угол.

Формула длины окружности:

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке дается определение окружности и круга, а также определение дуги, радиуса, хорды и диаметра окружности, рассматривается взаимное расположение точек и окружности, а также двух окружностей, решаются различные задачи по этой теме.

Видео:7 класс, 21 урок, ОкружностьСкачать

Окружность и круг

Окружность можно построить с помощью циркуля (рис. 1). Ножку с иголкой устанавливают в точку, а ножка с грифелем опишет замкнутую линию, которую называют окружностью.

Окружность – это множество точек, равноудаленных от заданной точки (точки О), которую называют центром окружности. Окружность разделит плоскость на 2 части. Ту часть плоскости, которая лежит внутри окружности вместе с самой окружностью, называют кругом. Точка О является как центром окружности, так и центром круга (рис. 2).

Рис. 2. Окружность и круг

Видео:Окружность. 7 класс.Скачать

Взаимное расположение окружности и точки

Точки могут лежать на окружности, т. е. принадлежать окружности. Точки А и В принадлежат окружности с центром в точке О (Рис. 3); точки О, Е и D не принадлежат окружности с центром в точке О; точки О, Е, А, В принадлежат кругу с центром в точке О, а точка D не принадлежит этому кругу.

Рис. 3. Окружность и круг с центром в точке О

Точки А и В делят окружность на две части (рис. 4), каждую из которых называют дугой окружности; точки А и В – концами дуг.

Рис. 4. Окружность

Видео:Длина окружности. Математика 6 класс.Скачать

Дуга, радиус, хорда, диаметр окружности

Дуга окружности – это часть окружности, ограниченная двумя точками. Пример. На окружности с центром в точке О отмечены точки А, В и С. Назовите дуги, на которые эти дуги делят окружность. Дуги с концами в точках А и В: дуга АВ, дуга АСВ. Дуги с концами в точках В и С: дуга ВС, дуга ВАС. Дуги с концами в точках А и С: дуга АС, дуга АВС. Отрезки ОА, ОВ соединяют центр окружности с точками, лежащими на окружности. Их называют радиусами (рис. 5).

Рис. 5. Радиусы окружности

Радиус – это расстояние от центра окружности до любой точки окружности. Радиусы одной окружности равны. Обозначают радиусы R или r. Отрезок, соединяющий две точки окружности, называют хордой. Хорду, проходящую через центр окружности, называют диаметром. Обозначают: d или D. Свойства диаметра: 1. диаметр – самая большая хорда. 2. d = 2R. Диаметр делит круг на два полукруга, а окружность – на две полуокружности

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Задача 1

Постройте окружность с центром в точке О и радиусом 4 см. Постройте прямую а так, чтобы она пересекла окружность в двух точках А и В (рис. 6). На каком расстоянии от центра окружности находятся точки А и В?

Рис. 6. Окружность с центром в точке О и радиусом 4 см

Так как расстояние между двумя точками – это длина отрезка с концами в этих точках, то нам необходимо найти длины отрезков ОА и ОВ. По определению отрезки ОА и ОВ – радиусы одной и той же окружности. Тогда ОА = ОВ = R= 4 см. Значит, на расстоянии 4 см находятся точки А и В от центра окружности.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Задача 2

Постройте отрезок АВ, равный 4 см. Постройте первую окружность с центром в точке А радиусом 3 см, и другую окружность с центром в точке В радиусом 2 см. Назовите точки пересечения окружностей точками Е и С (рис. 7). Чему равны длины отрезков АЕ, АС, ЕВ и ВС?

Рис. 7. Отрезок АВ

По определению, отрезок АЕ, АС – это радиусы первой окружности. АЕ = АС = = 2 см.

Видео:5 класс, 22 урок, Окружность и кругСкачать

Задача 3

Начертите отрезок СМ, равный 5 см. Постройте точку, удаленную от концов отрезка на 3 см. Сколько таких точек можно построить? Таких точек можно построить 2. Они будут лежать на пересечении двух окружностей с центром в точке С и с центром в точке М радиусом 3 см (рис. 8).

Рис. 8. Точки, удаленные от концов отрезка на 3 см

Список литературы

1. Н.Я. Виленкин. Учебник для 5 кл. общеобразовательных учреждений/ 17-е изд. – М.: Мнемозина, 2005.
2. Шевкин А.В. Текстовые задачи по математике: 5–6. – М.: Илекса, 2011. – 106 с.
3. Ершева А.П., Голобородько В.В. Вся школьная математика в самостоятельных и контрольных работах. Математика 5–6. – М.: Илекса, 2006. – 432 с.
4. Н.Н. Хлевнюк, М.В. Иванова. Формирование вычислительных навыков на уроках математики. 5–9 классы. – М.: Илекса, 2011. – 248 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

Учебник математики. 5 класс. Н.Я. Виленкин. № 850–856.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки [1] : эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Окружность разбивает плоскость на две части [2] — конечную внутреннюю и бесконечную внешнюю. Внутренность окружности называется кругом; граничные точки (то есть саму окружность) в зависимости от подхода, круг может включать или не включать.

Практическое построение окружности возможно с помощью циркуля.

Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.

Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.

Далее всюду буква R обозначает радиус окружности.

Видео:Чем отличается круг от окружностиСкачать

Содержание

Видео:Окружность. Круг. 5 класс.Скачать

Хорды, дуги и касательные [ править | править код ]

1 — секущая, 2 — хорда AB (отмечена красным), 3 — сегмент (отмечен зелёным), 4 — дуга

Прямая может иметь с окружностью не более двух общих точек.

Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D = 2 R , он делит окружность на две равные части и поэтому является её осью симметрии. Диаметр больше любой другой хорды [3] .

Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки) [3] .

Любые две несовпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.

Для заданной окружности имеют место следующие свойства [3] .

• Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
• Равным хордам соответствуют равные дуги, и наоборот.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности [4] .

Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности [5] .

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Углы [ править | править код ]

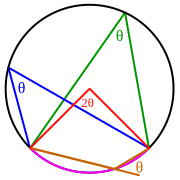
Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)

К расчёту длины дуги и хорды

Центральный угол — угол с вершиной в центре окружности. Центральный угол может быть принят как угловая мера дуги, на которую он опирается. Центральный угол, образуемый дугой окружности, равной по длине радиусу, в математике принимается в качестве единицы измерения углов, и называется радиан.

Из определения радиана следует, что длина L любой дуги окружности связана с центральным углом θ , опирающимся на эту дугу, простым соотношением [6] : L = R θ . (при этом длина хорды, стягивающей ту же дугу, равна 2 R sin ⁡ θ 2 L ). Поскольку длина окружности равна 2 π R , с ростом угла значение его радианной меры меняется от 0 до 2 π .

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Внешний угол для вписанного угла — угол, образованный одной стороной и продолжением другой стороны вписанного угла (угол θ коричневого цвета на рис.). Внешний угол для вписанного угла равен вписанному углу, опирающемуся на ту же хорду с другой стороны.

Угол между окружностью и прямой — угол между секущей прямой и одной из двух касательных к окружности в точке пересечения прямой и окружности.

• Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. Вписанный угол, опирающийся на дугу длиной в половину окружности, всегда прямой (равен 90°).
• Вписанный угол не меняет своей величины при перемещении его вершины вдоль окружности.
• Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

• Угол между двумя секущими, проведёнными из точки, лежащей вне окружности, равен полуразности мер дуг, лежащих между секущими.
• Угол между пересекающимися хордами равен полусумме мер дуги, лежащей в угле, и дуги напротив неё.
• Угол между касательной и хордой, имеющими общую точку, равен половине угловой меры дуги, стягиваемой хордой.

Видео:Окружность и круг, 6 классСкачать

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Определение окружности

• Отрезки в окружности

Видео:Что означает маркировка на шинах! Значение цифр и букв на резине.Скачать

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Эта точка называется центром окружности .

Видео:Тригонометрическая окружность. Как выучить?Скачать

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Видео:Математика 5 класс (Урок№26 - Окружность и круг. Сфера и шар.)Скачать

Дуга в окружности

Часть окружности, заключенная между двумя точками, называется дугой окружности .

Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .

Теорема 4:
Равные хорды стягивают равные дуги.

Если A B = C D , то ∪ A B = ∪ C D

Видео:Как найти центр круга с помощью подручных средств? ЛЕГКО.Скачать

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Градусная мара всей окружности равна 360 ° .

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ A C B – вписанный.

Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α

Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Длина окружности, длина дуги

Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .

Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Длина дуги окружности , на которую опирается центральный угол α равна:

l α = π R 180 ∘ ⋅ α

Видео:Квадрат в окружности или окружность в квадрате #ShortsСкачать

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.