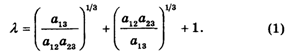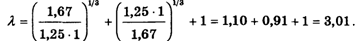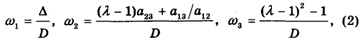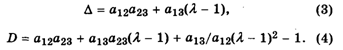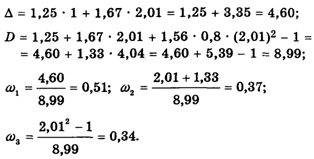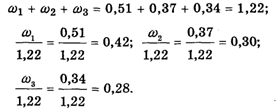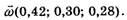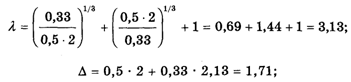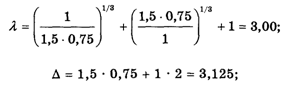Математические методы позволяют эффективно анализировать весьма сложные и большие системы, модели которых состоят из нескольких уровней. Например, известная модель мировой динамики Форрестера и Медоуза рассматривает ресурсы, население, уровень жизни, капиталовложения, загрязнение среды. Анализ состояния окружающей среды приводит к модели, уровнями которой могут быть: 1) типы загрязнителей SO2, NO4, CO2, CO, стоки вод, твердые отходы, земля), 2) способы очистки, 3) очистительные устройства. Изучение вопроса об общем благосостоянии страны целесообразно проводить по таким уровням: 1) экономика, оборона, здравоохранение; 2) отрасли промышленности; 3) ресурсы; 4) демография. Уровни располагаются по их значимости, т. е. образуют Иерархию. Анализ таких Иерархических систем, сводится прежде всего к тому, чтобы для каждого уровня выбрать Приоритеты и в соответствии с ними расположить объекты этого уровня. Основная цель анализа: выяснить, насколько влияют факторы самого низкого уровня на общую цель. Покажем на конкретном примере, как это делают Методом собственного вектора. Этот метод позволяет расположить рассматриваемые объекты по степени их значимости путем попарного сравнения по различным независимым признакам.
На должность юриста крупного предприятия претендуют трое (обозначим их А, В, С). Директор предприятия в большом затруднении, т. к. среди претендентов нет такого, кто превосходил бы остальных по всем параметрам. Один имеет больший опыт, зато другой имеет лучшее образование и опубликовал несколько научных работ; третий известен своей исключительной ответственностью и добросовестностью и т. д. Как выбрать Наилучшего по совокупности качеств? Тут директор вспомнил, что в институте экологии и права, где он учился, им преподавали математику, и, в частности, рассказывали о применении математических методов в теории принятия решений. Покопавшись в своих архивах, директор нашел лекции по математике и решил воспользоваться методом собственных векторов, применяемом при изучении иерархических систем.
Во-первых, он выбрал 3 основных критерия, по которым будут сравниваться кандидаты: профессионализм и опыт (критерий К1), ответственность и добросовестность (К2), организаторские способности (K3). По такому важному критерию как честность и порядочность претендентов сравнить было невозможно — у всех троих в характеристиках было написано по этому поводу практически одно и то же. Первая задача состояла в том, чтобы расположить эти критерии в порядке важности. Вторая задача состояла в том, чтобы сравнить кандидатов между собой по каждому из этих критериев, приписав каждому из них определенный балл.
Этап первый: сравнение критериев.
Исходя из своего жизненного и профессионального опыта, директор полагал, что критерий К1 важнее, чем критерии К2 и К3, причем, если сравнивать их количественно, в баллах, то К1 : К2
5 : 3. При этом, если, сравнивать последние два качества между собой, то они примерно равноценны, т. е. можно считать, что K2 : K3
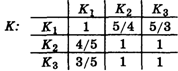
1 : 1. Далее директор составил матрицу К Размером 3´3, т. е. таблицу с тремя строками и тремя столбцами, куда занес отношения указанных баллов:
Видео:Собственные векторы и собственные значения матрицыСкачать
Число, стоящее на пересечении строки с номером I и столбца с номером J, обычно обозначают АIj. Поэтому у нас A11 = 1, A22 = 1, А33 = 1, A12 = 5/4, A13 = 5/3, А23 = 1, и т. д. Заметьте, что числа Aij и АJi являются взаимно обратными.
Все дальнейшие вычисления будем проводить вместе с директором приближенно, округляя до сотых долей, причем нам понадобятся только числа А12 = 1,25; A13 = 1,67 и A23 = 1.
Прежде всего находят так называемое Главное собственное число L матрицы К по формуле
Пользуясь калькулятором, получаем:
Теперь находим координаты W1, W2 и W3 так называемого Главного собственного вектора матрицы К по формулам
Подставляя сюда наши значения А12 = 1,25; A13 = 1,67;
A23 = 1, последовательно получаем:
Теперь собственный вектор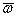 
(W1, W2, W3) Нужно Нормировать, т. е. каждую координату разделить на сумму всех координат. Имеем:
Сумма полученных чисел равна единице. Обозначим вектор, координатами которого являются эти числа, также буквой :
Этот вектор называется Вектором приоритетов. Согласно теории, качества К1, К2 и K3 можно расположить по приоритету с баллами 0,42; 0,30 и 0,28 соответственно.
Этап второй: сравнение претендентов по качеству К1. Из имеющихся у него документов (характеристик, рекомендаций, отзывов, научных публикаций) директор сумел сравнить между собой каждую пару претендентов по качеству К1. У него получилось А : В
Видео:Собственные векторы и собственные числа линейного оператораСкачать
1 : 2 (т. е. у В Балл в 2 раза выше, чем у А), А : С
2 : 1. Поэтому матрица К1 попарных сравнений получилась такая
Из нее видно, что А12 = 0,5, А13 = 0,33, А23 = 2. Подставляя эти числа в формулы (1)-(4), как и в предыдущем случае находим:
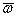
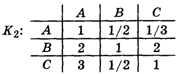
Итак, в этом случае вектор приоритетов будет (0,17; 0,48; 0,35), т. е., если сравнивать, претендентов по качеству К1, то они получают баллы 0,17, 0,48 и 0,35 соответственно.
Этап третий: сравнение претендентов по качеству K2:
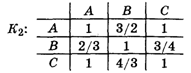
Как было видно из документов, каждые двое из претендентов работали некоторое время в одной и той же фирме и вели примерно одинаковые дела. Просмотрев последние и оценив качество исполнения, директор получил следующие отношения при попарном сравнении по критерию K2: А : В
3 : 4. Запишем матрицу К2 попарных сравнений:
Вектор приоритетов будет 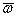(0,38; 0,26; 0,36), так что по качеству К2 претенденты получают баллы 0,38, 0,26 и 0,36 соответственно.
Этап четвертый: сравнение по качеству K3. Поскольку никто из претендентов прежде не находился на руководящей работе, то директор, исходя из весьма туманных соображений и своей интуиции, смог только оценить вероятность того, что тот или иной претендент станет хорошим руководителем. Получились вероятности 0,8, 0,7 и 0,6 соответственно. Таким образом, удалось обойтись без попарного сравнения. 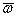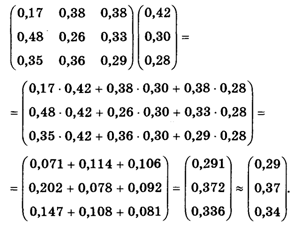Разделив каждое из указанных чисел на их сумму 0,8 + 0,7 + 0,6 = 2,1, находим вектор приоритетов: (0,38; 0,33; 0,29).
Этап пятый: получение окончательно результата. Согласно теории, окончательное распределение мест получается следующим образом. Составим из векторов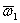 
, 
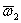
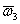
и 
матрицу 3´3, записав их координаты в столбцы:
Затем умножим эту матрицу на матрицу-столбец
Составленную из координат вектора 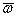. По правилу умножения матриц,
Итак, окончательное распределение мест следующее:
Претендент А набрал 0,29 балла, претендент В — 0,37 балла, претендент C — 0,34 балла. Метод собственного вектора отдал предпочтение претенденту В.
Видео:Собственные значения и собственные векторы матрицы (4)Скачать
Предупреждение: не попадайте под гипнотическое воздействие чисел! Несмотря на объективность математических методов, полученный результат нельзя рассматривать как истину в последней инстанции. Хотя бы потому, что выбор исходного материала (т. е. чисел А12, а13 и А23, входящих в матрицы К1, К2, К3), был в значительной степени субъективным. Поэтому и претендент С, имеющий примерно такой же балл, как и В, Также имеет шанс на успех, в особенности, если он не курит или согласен на меньшую зарплату.
1. Описанным методом можно сравнивать любое число кандидатов и по любому числу критериев, однако при большом их числе придется пользоваться другими формулами, приведенными, например, в книге Т. Саати «Принятие решений».
2. Вычислительные трудности, разумеется, можно переложить на ЭВМ.
3. Мы сознательно упростили ситуацию, опустив некоторые тонкости, связанные с оценкой метода. О них также можно прочитать в книге Т. Саати.
4. Еще раз отметим, в чем сила описанного метода. Сравнить каждые два объекта между собой по одному критерию довольно просто, и это дает возможность сравнительно легко заполнить матрицу попарных сравнений. Но затем, с помощью несложных вычислений, мы находим ответ уже на довольно трудный вопрос: какой из рассматриваемых объектов превосходит остальные по совокупности всех критериев.
Метод собственного вектора можно применять для анализа самых разнообразных проблем, о которых шла речь в начале параграфа. Например, автор упомянутой выше книги проанализировал этим методом рост терроризма для агентства по контролю над вооружениями и разоружением в Вашингтоне.
В качестве самостоятельной задачи попробуйте оценить претендентов на должность мэра Вашего города, выбрав критерии по своему усмотрению.
Нормы векторов и матриц
Пусть дано действительное (комплексное) линейное пространство X. Каждому вектору х ? X поставим в соответствие действительное число ||ж|| и назовем его нормой вектора х, если для любых векторов ж, у Е X и любого действительного (комплексного) числа а выполняются следующие аксиомы нормы:
Видео:Собственные значения и собственные векторыСкачать
Линейное пространство X при этом называется нормированным пространством.
В арифметическом пространстве Кп наиболее употребительными являются:
1) октаэдрическая норма
2) евклидова, или сферическая, норма
3) кубическая норма
Норму можно ввести в любом конечномерном пространстве. Если пространство евклидово (унитарное), то в нем можно ввести евклидову норму по формуле
Как правило, такая норма подразумевается в евклидовом (унитарном) пространстве и поэтому евклидовы (унитарные) пространства относят к нормированным пространствам.
В линейном пространстве (га х п)-матриц также рассматривают различные нормы. Наиболее употребительными являются:
Например, для матрицы
указанные нормы имеют следующие значения: 
Видео:Собственные векторы и собственные значенияСкачать
В линейном пространстве квадратных матриц порядка п кроме линейных операций, важную роль играет операция умножения матриц. В связи с этим в этом линейном пространстве предпочтение отдают нормам, согласованным с операцией умножения, а именно:
При этом норму матриц, не подчиняющуюся этому неравенству, иногда называют обобщенной нормой матриц.
Каждую (т х п)-матрицу А можно интерпретировать как оператор действующий из n-мерного арифметического пространства Кп в га-мерное арифметическое пространство Кт по формуле у = Ах, х G Кп, у е Кт. Если в Кп и Кт введены нормы, то желательно рассматривать норму матриц размера т х п, согласованную с векторными нормами в Кп и Кт:
Отметим, что это неравенство связывает сразу три нормы в трех разных линейных пространствах: в Кп, в Кш и в пространстве (т х п)- матриц.
Примером такой нормы является матричная норма, индуцированная векторной нормой (или подчиненная векторной норме) 
Приведем примеры норм, индуцированных различными векторными нормами.
- 1. Для октаэдрической векторной нормы ||t||i индуцированной является матричная норма ||A||i.
- 2. Для сферической векторной нормы ||а;||2 индуцированной является спектральная норма
где Ai, Аг, . Аг — собственные числа матрицы А*А.
3. Для кубической векторной нормы ||ж||оо индуцированной матричной нормой является норма ЦАЦоо.
Между различными матричными нормами существуют определенные соотношения. Особенно много таких соотношений приведено в [34].
Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать
🎥 Видео
7 4 Собственные векторы и собственные значенияСкачать
Собственные векторы и собственные числа линейного оператораСкачать
Айгенвектора и айгензначения | Сущность Линейной Алгебры, глава 10Скачать
Орт вектора. Нормировать вектор. Найти единичный векторСкачать
Собственные значения и собственные векторы. ПримерСкачать
Собственные значения и собственные векторы. ТемаСкачать
Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать
Диагональный вид матрицы. Приведение матрицы к диагональному виду. Собственные векторыСкачать
Собственные значения матрицыСкачать
Овчинников А. В. - Линейная алгебра - Собственные значения и собственные векторы линейного оператораСкачать
Квантовая механика 10 - Правило Борна. Нормирование векторов состояния.Скачать
Как разложить вектор по базису - bezbotvyСкачать
Лекция 2, Векторные и матричные нормы, унитарные матрицы, SVDСкачать
Практика 1. Часть 1. Собственные вектора и значения линейного оператора. Канонический вид.Скачать
