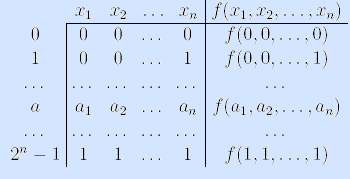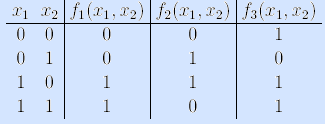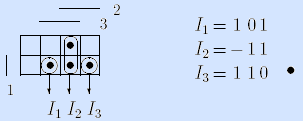1) Задание булевой функции таблицей истинности. Так называется таблица, состоящая из двух частей: в левой части перечисляются все наборы значений аргументов (булевы векторы пространства B n ) в естественном порядке, то есть по возрастанию значений чисел, представляемых этими векторами, а в правой части – значения булевой функции на соответствующих наборах.

Пример. Рассмотрим булеву функцию трех аргументов, называемую мажоритарной (или функцией голосования): она принимает значение 1 на тех и только тех наборах, в которых единиц больше, чем нулей (major – больший).

Так как левая часть таблицы истинности постоянна для всех функций с одинаковым числом аргументов, несколько таких функций могут быть заданы общей таблицей.

Теорема о числе булевых функций. Число различных булевых функций, зависящих от n переменных, равно 2 2 n .

Доказательство. Каждая булева функция определяется своим столбцом значений. Столбец является булевым вектором длины m=2 n , где n – число аргументов функции. Число различных векторов длины m (а значит и число булевых функций, зависящих от n переменных) равно 2 m =2 2 n . •

2) Задание булевой функции характеристическими множествами. Так называются два множества:

M 1 _f, состоящее из всех наборов, на которых функция принимает значение 1, то есть M 1 _f = <α B n :f(α) = 1>;

M 0 _f, состоящее из всех наборов, на которых функция принимает значение 0, то есть M 0 _f = <α B n :f(α) = 0>.

Пример (мажоритарная функция).

3) Задание булевой функции вектором ее значений.

Пример (мажоритарная функция).

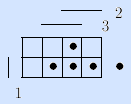
4) Задание булевой функции матрицей Грея. Булево пространство задается матрицей Грея, и наборы (клетки матрицы), на которых булева функция f(x₁, …, x_n) принимает значение 1, отмечаются и называются точками.

Пример (мажоритарная функция).

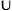
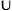
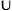
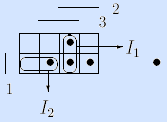
5) Интервальный способ задания булевой функции. Булеву функцию f(x₁, …, x_n) можно задать множеством интервалов I_f = <I₁, I₂, …, I_k>, объединение которых образует характеристическое множество M 1 _f, то есть I₁ I₂… I_k = M 1 _f. Множество интервалов I_f называется достаточным для функции f(x₁, …, x_n).

Пример. Мажоритарная функция может быть задана достаточным множеством I_f = <I₁, I₂, I₃> интервалов:

Здесь интервалы представлены троичными векторами и изображены на матрице Грея.

В отличие от предыдущих, интервальный способ задания функций многовариантен (одну и ту же булеву функцию можно представить разными множествами интервалов).

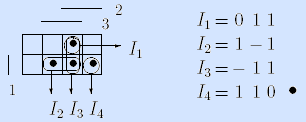
Пример. Зададим мажоритарную функцию другим достаточным множеством I’_f = <I₁, I₂, I₃, I₄> интервалов:

Очевидно, что это множество интервалов избыточно: первый интервал (011) можно удалить.

Определение. Интервал назовем допустимым для булевой функции, если на всех его наборах функция равна 1.

Примеры. I₁= – 1 1 – допустимый интервал для мажоритарной функции, I₂= 1 0 – – не допустимый.

Определение. Интервал I назовем максимальным для булевой функции f(x₁, …, x_n), если он является допустимым для этой функции, и не существует другого допустимого интервала I’, такого что I 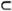I’.

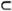
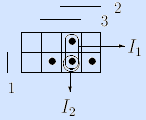
Пример. I₁= –11 является максимальным интервалом для мажоритарной функции, а допустимый интервал I₂ = 111 не является максимальным, так как I₂ I₁.

Пример. Зададим мажоритарную функцию множеством I»_f = <I₁ I₂, I₃> всех максимальных интервалов.

Определение. Точку булевой функции f(x₁, …, x_n) назовем ядерной, если она принадлежит ровно одному максимальному для этой функции интервалу. Максимальный интервал называется ядерным, если он содержит ядерную точку.

Пример. Для мажоритарной функции ядерными точками являются 011 (принадлежит только интервалу –11), 101 (принадлежит только интервалу 1 –1) и 110 (принадлежит только интервалу 11 –). Все максимальные интервалы этой функции являются ядерными. •

Очевидно, что все ядерные интервалы входят в любое достаточное множество функции, состоящее из максимальных интервалов.

6) Задание булевой функции формулами будет рассмотрено несколько позже.

Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Вектор-функции

Видео:Собственные векторы и собственные значения матрицыСкачать

Предел и непрерывность вектор-функции.

Понятие вектор-функции.

Если каждому значению (tin E), где (Esubsetmathbb), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).

Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.

В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.

Предел вектор-функции.

Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_<trightarrow t_>r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_<trightarrow t_> |r(t)-a|=0,label
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).

Рис. 20.1

Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_,a_,a_)), то
$$
lim_<trightarrow t_>r(t)=alabel
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label
$$

Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref, то выполняется условие eqref.

Обратно: если выполняются условия eqref, то из равенства eqref следует, что выполнено условие eqref. (bullet)

При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox trightarrow t_.nonumber
$$

Свойства пределов вектор-функций.

(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$

Если (r(t)rightarrow a) при (trightarrow t_), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_), то (f(t)r(t)rightarrow Aa) при (trightarrow t_), то есть
$$
lim_f(t)r(t)=lim_<trightarrow t_>f(t)lim_r(t).label
$$

(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref. (bullet)

(circ) По условию (r_(t)=a_+alpha_), где (a_i(t)rightarrow 0) при (trightarrow t_ (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_(t)+alpha_2(t)rightarrow 0) при (trightarrow t_), откуда следует eqref. Докажем формулу eqref. В силу свойств скалярного произведения
$$
(r_(t),r_2(t))-(a_1,a_2)=(alpha_(t),a_)+(alpha_(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_(t),alpha_(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).

Аналогично доказывается формула eqref, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)

Непрерывность вектор-функции.

Вектор-функцию (r(t)) называют непрерывной при (t=t_), если
$$
lim_<trightarrow t_>r(t)=r(t_0).label
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_) в силу эквивалентности условий eqref и eqref означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_).

Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_). Тогда условие eqref означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label
$$

Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_).

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Производная и дифференциал вектор-функции.

Производная вектор-функции.

Если существует (displaystyle lim_frac) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot(t_0)).

Таким образом,
$$
r'(t_)=lim_frac<r(t_+Delta t)-r(t_)>.label
$$
Аналогично вводится понятие второй производной
$$
r″(t_)=lim_frac<r'(t_+Delta t)-r'(t_)>nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_)=(x'(t_0),y'(t_0),z'(t_0))label
$$
Утверждение eqref следует из определения eqref и свойств пределов вектор-функций.

Аналогично, если существует (r″(t_)), то
$$
r″(t_)=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref, то есть вектор-функция (r(t)), имеющая производную в точке (t_), непрерывна при (t=t_).

(circ) Формулы eqref-eqref справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref. Пусть (Delta r_) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin
(r_,r_)’=displaystylelim_frac<(r_(t+Delta t),r_(t+Delta t))-(r_(t),r_(t))>=\
=lim_left[left(r_(t),frac<Delta r_(t)>right)+left(frac<Delta r_(t)>,r_2(t)right)+left(frac<Delta r_(t)>,Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
endnonumber
$$
так как (displaystyle frac<triangle mathrm_>rightarrow r_‘(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)

Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).

Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.

(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^)’=(C^)’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$

Дифференциал вектор-функции.

Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_), называют дифференцируемой при (t=t_), если ее приращение (Delta r=r(t_+Delta t)-r(t_)) в точке (t_) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).

Полагая (dt=Delta t), запишем равенство eqref в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac

.label (21)
$$

Замена переменного.

Если функция (t=t(s)) дифференцируема при (s=s_, t(s_)=t_), а вектор-функция (r(t)) дифференцируема в точке (t_), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_'(t_)t_‘(s_),label
$$

где индекс указывает, по какому переменному производится дифференцирование.

(circ) Функция (alpha(Delta(t))) в формуле eqref не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).

Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_+Delta s)-t(s_)rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref на (Delta sneq 0), получим
$$
frac=r'(t_0)frac+alpha(Delta t)frac.label
$$
Правая часть eqref имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref, и справедливо равенство eqref. Формулу eqref запишем кратко в виде равенства
$$
r_’=r_’t_’,label
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)

Видео:Функция. Множество значений функции. Практическая часть. 10 класс.Скачать

Теорема Лагранжа и локальная формула Тейлора для вектор-функции.

Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label
$$
для вектор-функции, вообще говоря, неверна.

(circ) В самом деле, пусть формула eqref верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)

Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label
$$

(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label
$$
Преобразуем левую часть неравенства eqref:
$$
begin
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
endnonumber
$$
Тогда равенство eqref примет вид
$$
|r(beta)-r(alpha)|^=(r(beta)-r(alpha),r'(xi))(beta-alpha).label
$$
Если (r(beta)=r(alpha)), то неравенство eqref справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref получим
$$
|r(beta)-r(alpha)|^leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref. (bullet)

Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_^frac<r^(t_)>(t-t_)^+varepsilon(t-t_),label
$$
где (varepsilon(t-t_0)=o((t-t_)^)) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_)^varepsilon_(t-t_)), где (varepsilon_(t-t_)rightarrow 0) при (trightarrow t_).Эта формула справедлива в предположении, что существует (r^(t_0)). Для доказательства формулы eqref достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).

Булевы функции

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Содержание

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

1 Понятие булевой функции

В курсе математического анализа изучаются функции, определённые на числовой прямой или на отрезке числовой прямой или на (гипер-) плоскости и т.п. Так или иначе область определения – непрерывное множество. В курсе дискретной математики изучаться должны функции, область определения которых – дискретное множество * . Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов. * Так мы и приходим к понятию булевой функции.

Определение 1 (Булева функция). Булевой функцией от n аргументов называется функция f из n -ой степени множества в множество .

Иначе говоря, булева функция – это функция, и аргументы и значение которой принадлежит множеству . Множество мы будем в дальнейшем обозначать через B .

Булеву функцию от n аргументов можно рассматривать как n -местную алгебраическую операцию на множестве B . При этом алгебра W >, где W – множество всевозможных булевых функций, называется алгеброй логики .

Конечность области определения функции имеет важное преимущество – такие функции можно задавать перечислением значений при различных значениях аргументов. Для того, чтобы задать значение функции от n переменных, надо определить значения для каждого из 2 n наборов. Эти значения записывают в таблицу в порядке соответствующих двоичных чисел. В результате получается таблица следующего вида:

x 1	x 2	.	x n- 1	x n	f
0	0	.	0	0	f(0,0. 0,0)
0	0	.	0	1	f(0,0. 0,1)
0	0	.	1	0	f(0,0. 1,0)
0	0	.	1	1	f(0,0. 1,1)
.	.	.	.	.	.
1	1	.	0	0	f(1,1. 0,0)
1	1	.	0	1	f(1,1. 0,1)
1	1	.	1	0	f(1,1. 1,0)
1	1	.	1	1	f(1,1. 1,1)

Раз у нас есть стандартный порядок записывания наборов, то для того, чтобы задать функцию, нам достаточно выписать значения f (0,0. 0,0) , f (0,0. 0,1) , f (0,0. 1,0) , f (0,0. 1,1). f (1,1. 0,0) , f (1,1. 0,1) , f (1,1. 1,0) , f (1,1. 1,1). Этот набор называют вектором значений функции .

Таким образом, различных функций n переменных столько, сколько различных двоичных наборов длины 2 n * . А их 2 в степени 2 n .

Множество B содержит два элемента – их можно рассматривать как булевы функции от нуля (пустого множества) переменных – константу 0 и константу 1 .

Функций от одной переменной четыре: это константа 0, константа 1, тождественная функция , т.е. функция, значение которой совпадает с аргументом и так называемая функция « отрицание ». Отрицание будем обозначать символом ¬ как унарную операцию. Приведём таблицы этих четырёх функций:

x	0	x	¬ x	1
0	0	0	1	1
1	0	1	0	1

Как видим, функции от некоторого числа переменных можно рассматривать как функции от большего числа переменных. При этом значения функции не меняется при изменении этих «добавочных» переменных. Такие переменные называются фиктивными , в отличие от остальных – существенных .

Определение 2 (Фиктивные и существенные переменные). Переменная x i называется фиктивной (несущественной) переменной функции f ( x 1 ,···,x n ), если f ( x 1 ,···,x i- 1 ,0 ,x i+ 1 ,···,x n ) = f ( x 1 ,···,x i- 1 ,1 ,x i+ 1 ,···,x n ) для любых значений x 1 ,···,x i- 1 ,x i+ 1 ,···,x n . Иначе переменная x i называется существенной .

Функций от двух аргументов шестнадцать. Наиболее употребимые из этих функций (только те, которые существенно зависят от обеих переменных) мы приводим в следующей таблице:

x 1	x 2	x 1 & x 2	x 1 Ъ x 2	x 1 Й x 2	x 1 Е x 2	x 1 є x 2	x 1 | x 2
0	0	0	0	1	0	1	0
0	1	0	1	1	1	0	1
1	0	0	1	0	1	0	1
1	1	1	1	1	0	1	1

Эти функции записываются как бинарные операции в инфиксной нотации. x 1 & x 2 называется конъюнкцией , x 1 Ъ x 2 – дизъюнкцией , x 1 Й x 2 – импликацией , x 1 є x 2 – эквивалентностью , x 1 Е x 2 – суммой по модулю 2 , x 1 | x 2 – штрихом Шеффера .

Значения 0 и 1 часто интерпретируют как «ложь» и «истину». Тогда понятным становится название функции «отрицание» – она меняет «ложь» на «истину», а «истину» на «ложь». Отрицание читается как «не». Конъюнкция читается обычно как «и» – действительно, конъюнкция равна 1 тогда и только тогда, когда равны 1 и первая и вторая переменная. * Кроме x 1 & x 2 часто используют обозначение x 1 Щ x 2 или x 1 · x 2 или x 1 x 2 или min( x 1 ,x 2 ). Дизъюнкция читается «или» – дизъюнкция равна 1 тогда и только тогда, когда равны 1 первая или вторая переменная. * Импликация выражает факт, что из x 1 следует x 2 . * Импликацию часто также обозначают x 1 ® x 2 .

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

2 Суперпозиция функций

Определение 3 (Суперпозиция функций). Суперпозицией булевых функций f 0 и f 1 . f n называется функция f ( x 1 . x m ) = f 0 ( g 1 ( x 1 . x m ) . g k ( x 1 . x m )), где каждая из функций g i ( x 1 , . x m ) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f 1 . f n .

Пример 1 (суперпозиция функций).

Функция f ( x,y ) = ¬ ( x & y ) является суперпозицией функций ¬ и &. Функция g ( x,y ) = x Е ( x Ъ y ) является суперпозицией функций Е и Ъ . Функция h ( x,y,z ) = ( x & y ) Е z является суперпозицией функций Е и &. Построим таблицы этих функций.

Суперпозицию ( x & y ) Е ( ¬x Ъ ¬y ) можно прочитать как « x и y плюс не x или не y ».

Следующие соотношения могут быть проверены прямым сравнением значений функций в левой и правой части соотношения на всевозможных наборах аргументов.

1. x & y = y & x
2. x Ъ y = y Ъ x
3. x Е y = y Е x
4. x & ( y & z ) = ( x & y ) & z
5. x Ъ ( y Ъ z ) = ( x Ъ y ) Ъ z
6. x Е ( y Е z ) = ( x Е y ) Е z
7. x Ъ ( y & z ) = ( x Ъ y ) & ( x Ъ z )
8. x & ( y Ъ z ) = ( x & y ) Ъ ( x & z )
9. ¬¬x = x
10. ¬ ( x & y ) = ¬x Ъ ¬y
11. ¬ ( x Ъ y ) = ¬x & ¬y
12. x & x = x
13. x & ¬x = 0
14. x & 0 = 0
15. x & 1 = x
16. x Ъ x = x
17. x Ъ ¬x = 1
18. x Ъ 0 = x
19. x Ъ 1 = 1
20. x Е y = ( x & ¬y ) Ъ ( ¬x & y )
21. x Й y = ¬x Ъ y
22. x є y = ( x & y ) Ъ ( ¬x & ¬y )

Видео:Собственные значения и собственные векторыСкачать

3 Двойственные функции

Определение 4 (Двойственная функция). Функция g ( x 1 . x n ) = ¬f ( ¬x 1 . ¬x n ) называется двойственной функцией к функции f и обозначается f * .

Пример 2 (двойственные функции).

( x & y ) * = ¬ ( ¬x & ¬y ) = x Ъ y .

Предложение 1 (Двойственная к двойственной функции). Функция, двойственная к двойственной функции f равна самой функции f.

Доказательство. f * ( x 1 . x n ) * = ( ¬f ( ¬x 1 . ¬x n )) * = *
= ¬¬f ( ¬¬x 1 . ¬¬x n ) = *
= f ( x 1 . x n ) *

Рассмотрим, что происходит с таблицей двойственной функции. Замена набора ( x 1 . x n ) на ( ¬x 1 . ¬x n ) соответствует «переворачиванию» таблицы. Действительно, наборы ( x 1 . x n ) и ( ¬x 1 . ¬x n ) расположены симметрично относительно середины таблицы. Теперь остаётся применить операцию ¬ к результату функции, т.е. поменять 0 на 1 и 1 на 0. Т.о. вектор значений функции, двойственной к исходной, получается из вектора исходной функции переворачиванием и заменой 0 на 1, а 1 на 0.

Пример 3 (вектор двойственной функции).

Функции x & y и x Ъ y , задаваемые векторами значений (0,0,0,1) и (0,1,1,1) двойственны друг к другу. Также двойственными являются x Е y и x є y , задаваемые векторами (0,1,1,0) и (1,0,0,1). Каждая из функций x и ¬x (векторы (0,1) и (1,0) соответственно) двойственна сама себе.

Теорема 1 (Принцип двойственности). Функция, двойственная к суперпозиции функций, равна суперпозиции двойственных функций. Точнее: f 0 ( f 1 . f m ) * = f 0 * ( f 1 * . f m * )

Доказательство. f 0 ( f 1 ( x 1 . x n ) . f m ( x 1 . x n )) * =

= ¬f 0 ( f 1 ( ¬x 1 . ¬x n ) . f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬¬f 1 ( ¬x 1 . ¬x n ) . ¬¬f m ( ¬x 1 . ¬x n )) =	*
= ¬f 0 ( ¬f 1 * ( x 1 . x n ) . ¬f m * ( x 1 . x n )) =	*
= f 0 * ( f 1 * ( x 1 . x n ) . f m * ( x 1 . x n ))	*

Видео:Функция. Область определения и область значений функцииСкачать

4 Разложение функции по переменным

x s =

м ¬x, если s =0 н о x, если s =1

.

Теорема 2 (Разложение в дизъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m )

Доказательство. Покажем, что для любого набора значений переменных ( x 1 . x n ,x n+ 1 . x m ) значения левой и правой частей совпадают. Возьмём фиксированный набор ( x 1 . x n ,x n+ 1 . x m ). Рассмотрим выражение x 1 s 1 & . & x n s n . Если одно из значений x i s i равно 0, то и всё выражение равно 0. Тогда и выражение x 1 s 1 & . & x n s n & f ( s 1 . s n ,x n+ 1 . x m ) равно 0. Единице же выражение x 1 s 1 & . & x n s n равно только в том случае, если s 1 = x 1 , . s n = x n . При этом f ( s 1 . s n ,x n+ 1 . x m ) = f ( x 1 . x n ,x n+ 1 . x m ) Таким образом, значение правой части всегда равно равно f ( x 1 . x m ), то есть значению левой части.

Теорема 3 (Разложение в конъюнкцию). Любую функцию f ( x 1 . x m ) для любого n (1 Ј n Ј m ) можно представить в виде f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x n ¬ s n Ъ f ( s 1 . s n ,x n+ 1 . x m )

Разложения по всем переменным дают суперпозицию конъюнкции, дизъюнкции и отрицания.

Следствие 1 (Совершенная дизъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: *

f ( x 1 . x m ) = x 1 s 1 & . & x m s m & f ( s 1 . s m ) = *

= x 1 s 1 & . & x m s m

Следствие 2 (Совершенная конъюнктивная нормальная форма).

Любая функция f может быть представлена в следующей форме: * f ( x 1 . x m ) = x 1 ¬ s 1 Ъ . Ъ x m ¬ s m

Таким образом, любая булева функция может быть представлена суперпозицией конъюнкции, дизъюнкции и отрицания. Разложение по всем переменным в дизъюнкцию называется совершенной дизъюнктивной нормальной формой функции, а в конъюнкцию – совершенной конъюнктивной нормальной формой . *

Совершенная дизъюнктивная и конъюнктивная нормальная формы дают способ представления булевой функции через суперпозицию конъюнкции, дизъюнкции и отрицания если у нас есть таблица значений функции.

Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.

Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.

Пример 4 (совершенная дизъюнктивная нормальная форма).

Построим совершенную дизъюнктивную нормальную форму функции, заданной следующей таблицей.

x	y	z	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Наборы, на которых функция равна 1 – это (0,1,1), (1,0,1), (1,1,0), (1,1,1). Первый набор даёт конъюнкцию ¬x & y & z , второй – x & ¬y & z , третий – x & y & ¬z , четвёртый – x & y & z . В результате получаем ( ¬x & y & z ) Ъ ( x & ¬y & z ) Ъ ( x & y & ¬z ) Ъ ( x & y & z ).

🎬 Видео

ОБЛАСТЬ ЗНАЧЕНИЙ ФУНКЦИИ - Алгебра 7 класс - Теория функцийСкачать

Функции. Урок №4. Область значений функции.Скачать

Математика это не ИсламСкачать

Как найти область определения функции? #shortsСкачать

7 4 Собственные векторы и собственные значенияСкачать

Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Область значений функцииСкачать

Коллинеарность векторовСкачать

Квантовая механика 8 - Операторы. Собственные векторы и собственные значения.Скачать