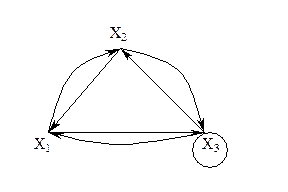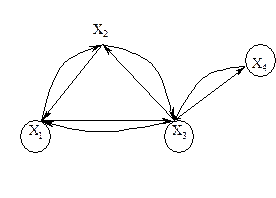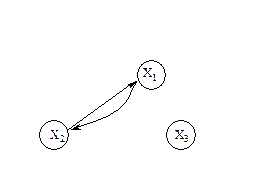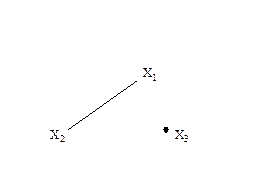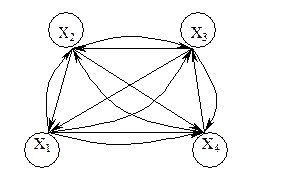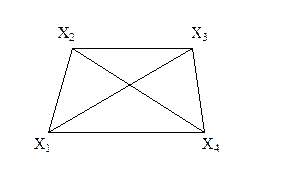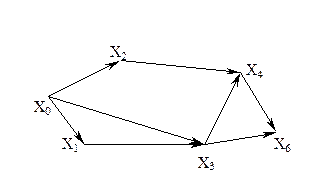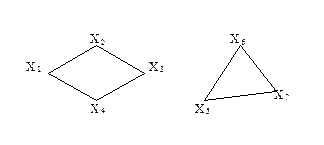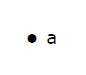Вектор, компонентами, которого являются окружения всех вершин графа, называют вектором степеней второго порядка.
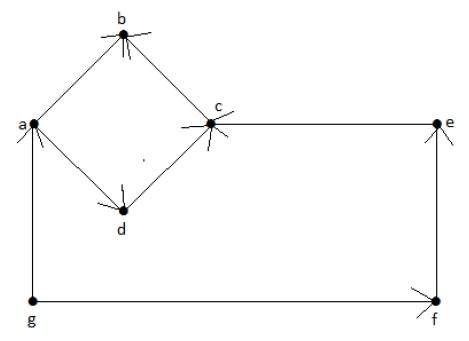
У графа Г на рисунке вектор степеней второго порядка равен ((3), (2, 3), (2, 3), (2, 2), (2, 2), (2, 2, 1)).
Чтобы различать эти два вектора, простой вектор степеней иногда называют вектором степеней первого порядка.
Из сохранения отношения смежности при изоморфизме следует, что векторы степеней изоморфных графов совпадают.
Рис. 82. Неизоморфные графы Г1 и Г2 имеют одинаковые векторы степеней
Иначе говоря, для изоморфизма графов необходимо равенство векторов степеней.
Обратное утверждение неверно.
Равенства векторов степеней недостаточно для изоморфизма графов.
Конечно, в некоторых случаях, изоморфизм графов все-таки следует из равенства векторов степеней. Например, два графа с одинаковым числом вершин изоморфны, если оба пусты, или оба полные, или каждый содержит в точности по одному ребру.
Графический вектор может задавать неизоморфные графы.
Например, вектор (2, 2, 2, 2, 2, 2) — графический, он является вектором степеней графа, причем даже не одного, а двух — неизоморфных графов.
Мало того, что графы Гі и Гг неизоморфны. Первый граф распадается на два, несоединенных между собой «куска». Такой граф называется несвязным, а два «куска» графа — это две компоненты связности.
Пример графов Гі и Гг показывает, что по вектору степеней, вообще говоря, нельзя даже определить, связный граф или не связный. Если граф не связный, то с помощью этого вектора не удастся вычислить точное число компонент связности графа.
Не спасает положения и вектор степеней второй ступени: и эти векторы у графов Г і и Гг одинаковые.
Однако в следующем примере (графы Гз и Гд) вектор степеней второго порядка поможет справиться с ситуацией.

Рис. 83. Векторы степеней у Гз и Гд совпадают
Вектор степеней графа Гз равен вектору степеней графа Гд и равен (2, 2, 2, 3, 3).
Вектор степеней второго порядка графа Г з равен ((3, 3), (3, 2), (3, 2), (3, 2, 1), (3, 2, 2, 1)).
Вектор степеней второго порядка для графа Гд другой: ((3, 3), (3, 3), (3, 3), (2, 2, 2), (2, 2, 2)).
Эти векторы различны, и, следовательно, графы Гз и Гдне изоморфны.
То, что эти графы не изоморфны, видно, впрочем, и из других соображений. Например, в графе Гз есть только один цикл, состоящий из трех ребер, а в графе Гд таких циклов два.
Рис. 84. Помеченные графы R и Ге— равные
- Степень вершины графа. Число ребер графа.
- Теория графов — основы
- точка
- пример
- Линия
- пример
- пример
- пример
- график
- Пример 1
- Пример 2
- петля
- Пример 1
- Пример 2
- Степень вершины
- Степень вершины в неориентированном графе
- Пример 1
- Пример 2
- Степень вершины в ориентированном графе
- Степень графа
- Степень графа
- Пример 1
- Пример 2
- Кулон Вертекс
- пример
- Изолированная вершина
- пример
- смежность
- Пример 1
- Пример 2
- Параллельные края
- Мульти График
- Пример 1
- Пример 2
- Степень последовательности графика
- Пример 1
- Пример 2
- 📹 Видео
Видео:Графы, вершины, ребра, инцидентность, смежностьСкачать

Степень вершины графа. Число ребер графа.
Теория графов
Графы
Бинарное отношение на конечном множестве X есть ориентированный конечный граф (орграф) RÍX 2 . Таким образом, всякий орграф определяется множествами:
X=<X1,X2,…,Xn> – множеством вершин графа и множеством упорядоченных пар (кортежей)
Общепринято обозначать орграфы в виде
X – множество вершин орграфа;
U – множество дуг орграфа, или в виде
ГX = <Гx1,Гx2,…,Гxn> – множество образов элементов множества X, т.е. отображение X в X, понимая термин отображения как точечно-множественное отображение.
Наряду с орграфами в приложениях рассматриваются неориентированные графы. Неориентированный граф является частным случаем орграфа, в котором для каждой дуги , т.е. бинарное отношение R обладает свойством симметрии. Если, кроме того, бинарное отношение R обладает свойством рефлексивности, то соответствующий ему ориентированный граф есть орграф-толерантность, содержащий дуги типа петля для всех вершин графа.
При геометрической реализации неориентированного графа вместо двух дуг и , соединяющих вершины Xi и Xj, употребляется одно ребро (Xi,Xj), не имеющее ориентации. На рис. 3.1.1 приведены геометрические реализации орграфов (слева) и их неориентированных аналогов – неориентированных графов (справа). G(X,U), если X’ÍX; U’ÍU, т.е. подграф G’ получим из графа G, если уберем какое-либо число вершин или ребер (дуг).
Две вершины графа называются смежными, если они соединены с началом другой.
Дуги называются смежными, если конец одной из них совпадает с началом другой.
Некоторая последовательности смежных дуг называется путем, а последовательность смежных ребер называется цепью.
Замкнутый путь называется контуром, а замкнутая цепь – циклом.
Сформулированные определения удобно представить в виде следующей таблицы:
| Ориентированный граф | Неориентированный граф |
| Дуга | Ребро |
| Путь | Цепь |
| Контур | Цикл |
Рассмотрим еще некоторые определения, которые нам понадобятся в дальнейшем. Пусть (цепь) называется элементарным, если он проходит через вершины графа по одному разу.
Путь (цепь) называется простым, если он проходит через дуги графа по одному разу. В противном случае путь (цепь) называется составным. Аналогично определяются и простые контуры и циклы.
Цепь (цикл) называется гамильтоновой, если она проходит через все вершины графа по одному разу, т.е. элементарная цепь, проходящая через все вершины графа, есть гамильтонова цепь.
Цепь (цикл) называется эйлеровой, если она проходит через все ребра по одному разу, т.е. простая цепь (цикл), содержащая все ребра графа есть эйлерова цепь (цикл).
Аналогично определяются гамильтоновы и эйлеровы путь и контуры.
Симметричный граф Неориентированный граф
Граф-толерантность Неориентированный граф
Граф-толерантность Неориентированный граф
Граф-декартово произведение Неориентированный полный граф
(с полным насыщением)
Степень вершины графа. Число ребер графа.
Вершина Xi называется инцидентной дуге (ребру) графа, если она является началом или концом этой дуги (ребра).
Степенью вершины графа называют число дуг (ребер), инцидентных данной вершине. Степень обозначается P(Xi).
Для ориентированного графа различают полустепень захода P + — число дуг, входящих в данную вершину, и полустепень исхода P — — число дуг, выходящих из данной вершины. Степень вершины ориентированного графа составит сумма полустепеней исхода и захода.
Если для некоторой вершины ориентированного графа полустепень захода некоторой вершины P + =0 и при этом полустепень исхода P — ¹0, то вершина называется входом графа.
Если для некоторой вершины ориентированного графа P — =0, а P + ¹0, то вершина называется выходом графа.
Граф, изображенный на рис. 3.1.2, имеет один вход – вершину X0
Число ребер графа N связано со степенями его вершин следующим соотношением:
N= 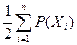
где n – число вершин графа. Отсюда следует справедливость следующих утверждений:
1) Сумма степеней вершин любого графа четна;
2) Для любого графа число вершин, имеющих нечетные степени, четно;
3) Для однородного графа, т.е. графа, все степени вершин которого одинаковы и равны r, N= 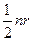
4) Для полного графа, т.е. графа, в котором каждая пара вершин соединена ребром или дугой, P(Xi)=n-1, а N= 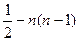
Некоторой противоположностью полному графу является нуль-граф, не имеющий ребер или дуг и состоящий из изолированных вершин. Очевидно, степени верши нуль-графа равны 0.
Связность
Граф называется связным, если множество его вершин нельзя разбить на два или более подмножеств так, чтобы ни одна вершины одного подмножества не отображалась в вершину другого. В противном случае граф называется несвязным. Число подмножеств всех вершин графа, называется числом компонент связности для несвязного графа.
Существует другое определение связности графа. Граф называется связным, если две любые его вершины можно соединить цепью. Граф (рис. 3.1.3) является несвязным с двумя компонентами.
Ребро графа называется перешейком, или связующей линией, если его удаление приводит к тому, что граф становится несвязным. На рис. 3.1.4 изображены три связных неориентированных графа, причем граф 1 не имеет ни одного перешейка, 2 содержит один перешеек (отмечен жирной линией), граф 3 целиком состоит из одних перешейков. Такой граф (3) называется деревом.
Видео:Степени вершина графаСкачать

Теория графов — основы
График — это диаграмма точек и линий, соединенных с точками. У него есть по крайней мере одна линия, соединяющая набор из двух вершин без вершин, соединяющих себя. Понятие графов в теории графов опирается на некоторые основные термины, такие как точка, линия, вершина, ребро, степень вершин, свойства графов и т. Д. Здесь, в этой главе, мы рассмотрим эти основы теории графов.
Видео:Графы | Степень вершины | Лемма о рукопожатиях | Компоненты связностиСкачать

точка
Точка — это конкретная позиция в одномерном, двухмерном или трехмерном пространстве. Для лучшего понимания точку можно обозначить алфавитом. Его можно обозначить точкой.
пример
Здесь точка — это точка с именем «а».
Видео:Графы.Вступление. Виды графов,степень вершин, ориентированный графСкачать

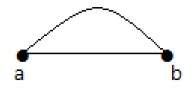
Линия
Линия — это связь между двумя точками. Это может быть представлено сплошной линией.
пример
Здесь «а» и «б» являются точками. Связь между этими двумя точками называется линией.
Вершина — это точка, где встречаются несколько линий. Это также называется узлом . Подобно точкам, вершина также обозначается алфавитом.
пример
Здесь вершина названа с алфавитом «а».
Ребро — это математический термин для линии, соединяющей две вершины. Многие ребра могут быть сформированы из одной вершины. Без вершины ребро не может быть сформировано. Для ребра должна быть начальная и конечная вершина.
пример
Здесь «a» и «b» — две вершины, и связь между ними называется ребром.
Видео:Способы задать граф. Матрица векторов смежностиСкачать

график
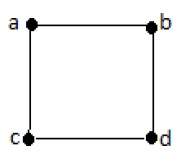
Граф ‘G’ определяется как G = (V, E), где V — множество всех вершин, а E — множество всех ребер графа.
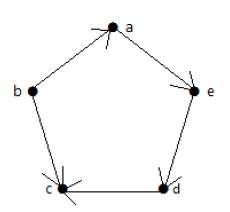
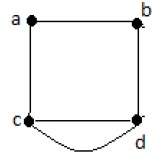
Пример 1
В приведенном выше примере ab, ac, cd и bd являются ребрами графа. Аналогично, a, b, c и d являются вершинами графа.
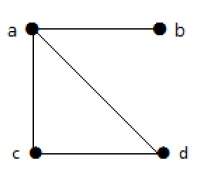
Пример 2
В этом графе есть четыре вершины a, b, c и d и четыре ребра ab, ac, ad и cd.
Видео:Графы. Степень вершины графа. Подготовка к олимпиаде по математикеСкачать

петля
В графе, если ребро нарисовано от вершины к себе, это называется циклом.
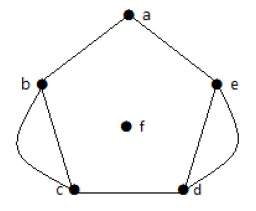
Пример 1
На приведенном выше графике V — вершина, для которой у нее есть ребро (V, V), образующее петлю.
Пример 2
В этом графе есть две петли, которые сформированы в вершине a, и вершине b.
Видео:4.8 Степени вершин графовСкачать

Степень вершины
Это число вершин, смежных с вершиной V.
Обозначение — град (V).
В простом графе с n числом вершин степень любых вершин равна —
Вершина может образовывать ребро со всеми остальными вершинами, кроме самой себя. Таким образом, степень вершины будет равна числу вершин в графе минус 1 . Это 1 для собственной вершины, поскольку она не может образовывать петлю сама по себе. Если в любой из вершин есть петля, то это не простой граф.
Степень вершины можно рассматривать по двум случаям графов —
- Ненаправленный граф
- Направленный граф
Видео:5-часовой веб по ГРАФАМСкачать

Степень вершины в неориентированном графе
Ненаправленный граф не имеет направленных ребер. Рассмотрим следующие примеры.
Пример 1
Посмотрите на следующий график —
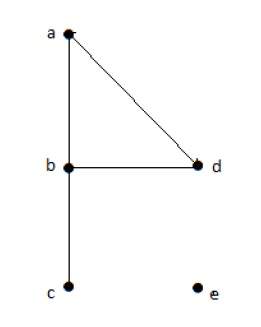
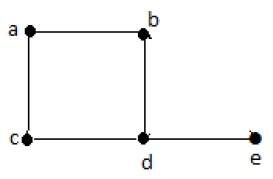
На приведенном выше неориентированном графике
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
Итак, «c» — это вершина с кулоном .
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Так что «е» — изолированная вершина .
deg (a) = 2, поскольку в вершине ‘a’ встречаются 2 ребра.
deg (b) = 3, поскольку в вершине ‘b’ встречаются 3 ребра.
deg (c) = 1, поскольку в вершине ‘c’ сформировано 1 ребро
Итак, «c» — это вершина с кулоном .
deg (d) = 2, поскольку в вершине ‘d’ встречаются 2 ребра.
deg (e) = 0, так как в вершине ‘e’ есть 0 ребер.
Так что «е» — изолированная вершина .
Пример 2
Посмотрите на следующий график —
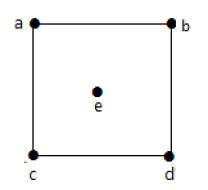
На приведенном выше графике
deg (a) = 2, deg (b) = 2, deg (c) = 2, deg (d) = 2 и deg (e) = 0.
Вершина «е» является изолированной вершиной. Граф не имеет никакой вершины.
Видео:РАЗБОР ЗАДАЧИ - ТЕОРЕМА 1.Скачать

Степень вершины в ориентированном графе
В ориентированном графе каждая вершина имеет степень и степень.
Степень графа
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень вершины V — это количество ребер, входящих в вершину V.
Обозначение — град — (V).
Степень графа
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Отступ вершины V — это число ребер, выходящих из вершины V.
Обозначение — град + (V).
Рассмотрим следующие примеры.
Пример 1
Посмотрите на следующий ориентированный граф. Вершина «а» имеет два ребра, «ad» и «ab», которые идут наружу. Следовательно, его степень равна 2. Аналогично, существует ребро «ga», идущее к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 2 | |
| б | 2 | 0 |
| с | 2 | 1 |
| d | 1 | 1 |
| е | 1 | 1 |
| е | 1 | 1 |
| г | 0 | 2 |
Пример 2
Посмотрите на следующий ориентированный граф. Вершина ‘a’ имеет ребро ‘ae’, идущее наружу от вершины ‘a’. Следовательно, его степень равна 1. Аналогично, у графа есть ребро «ba», приближающееся к вершине «a». Следовательно, степень «а» равна 1.
Степень и степень других вершин показаны в следующей таблице:
| темя | полустепень захода | полустепень |
|---|---|---|
| 1 | 1 | |
| б | 0 | 2 |
| с | 2 | 0 |
| d | 1 | 1 |
| е | 1 | 1 |
Видео:Диаметр графа. Радиус. Эксцентриситет. ЦентрСкачать

Кулон Вертекс
Используя степень вершины, мы получаем два специальных типа вершин. Вершина с первой степенью называется нерешенной вершиной.
пример
Здесь, в этом примере, вершина ‘a’ и вершина ‘b’ имеют соединенное ребро ‘ab’. Таким образом, что касается вершины «a», то к вершине «b» имеется только одно ребро, и аналогично по отношению к вершине «b» есть только одно ребро к вершине «a». Наконец, вершина ‘a’ и вершина ‘b’ имеют степень как единицу, которая также называется висячей вершиной.
Видео:ВСЯ теория по графам для олимпиадСкачать

Изолированная вершина
Вершина с нулевой степенью называется изолированной вершиной.
пример
Здесь вершина «a» и вершина «b» не имеют связи между собой, а также с любыми другими вершинами. Таким образом, степень обеих вершин ‘a’ и ‘b’ равна нулю. Они также называются изолированными вершинами.
Видео:Математика это не ИсламСкачать

смежность
Вот нормы смежности —
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
В графе две вершины называются смежными, если между двумя вершинами есть ребро. Здесь смежность вершин поддерживается одним ребром, соединяющим эти две вершины.
В графе два ребра называются смежными, если между двумя ребрами есть общая вершина. Здесь смежность ребер поддерживается единственной вершиной, соединяющей два ребра.
Пример 1
На приведенном выше графике —
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
«a» и «b» — это смежные вершины, так как между ними есть общее ребро «ab».
«a» и «d» являются смежными вершинами, так как между ними есть общее ребро «ad».
ab ‘и’ be ‘- смежные ребра, так как между ними есть общая вершина’ b ‘.
be ‘и’ de ‘- смежные ребра, так как между ними есть общая вершина’ e ‘.
Пример 2
На приведенном выше графике —
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
a ‘и’ d ‘являются смежными вершинами, так как между ними есть общее ребро’ ad ‘.
‘c’ и ‘b’ являются смежными вершинами, так как между ними есть общее ребро ‘cb’.
‘ad’ и ‘cd’ являются смежными ребрами, так как между ними есть общая вершина ‘d’.
ac ‘и’ cd ‘являются смежными ребрами, так как между ними есть общая вершина’ c ‘.
Видео:24 Сумма степеней вершин графа вдвое больше количества его рёберСкачать

Параллельные края
В графе, если пара вершин соединена более чем одним ребром, то эти ребра называются параллельными ребрами.
На приведенном выше графике «a» и «b» — это две вершины, которые соединены между собой двумя ребрами «ab» и «ab». Так это называется параллельным ребром.
Видео:Собственные значения и собственные векторы матрицы (4)Скачать

Мульти График
Граф, имеющий параллельные ребра, называется мультиграфом.
Пример 1
На приведенном выше графике есть пять ребер «ab», «ac», «cd», «cd» и «bd». Поскольку ‘c’ и ‘d’ имеют два параллельных ребра между ними, это мультиграф.
Пример 2
На приведенном выше графике вершины «b» и «c» имеют два ребра. Вершины ‘e’ и ‘d’ также имеют два ребра между ними. Следовательно, это мультиграф.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

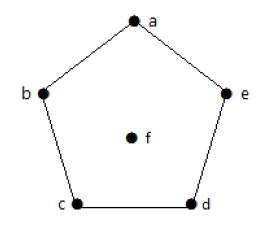
Степень последовательности графика
Если степени всех вершин в графе расположены в порядке убывания или возрастания, то полученная последовательность называется последовательностью графа графа.
Пример 1
| темя | б | с | d | е | |
|---|---|---|---|---|---|
| Присоединенный к | До нашей эры | объявление | объявление | с, Ь, е | d |
| степень | 2 | 2 | 2 | 3 | 1 |
На приведенном выше графике для вершин последовательность степеней равна .
Пример 2
| темя | б | с | d | е | е | |
|---|---|---|---|---|---|---|
| Присоединенный к | быть | а, с | б, г | с, е | объявление | — |
| степень | 2 | 2 | 2 | 2 | 2 | 0 |
На приведенном выше графике для вершин последовательность степеней равна .
📹 Видео
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

39 Сумма степеней вершин графа вдвое больше числа его рёберСкачать

Орт вектора. Нормировать вектор. Найти единичный векторСкачать

Графы 2. Полные и связные графыСкачать

ГрафыСкачать