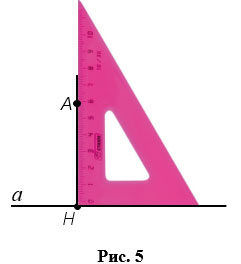Перпендикулярный треугольник 7 класс (6 видео)

Перпендикуляр к прямой

Возьмем прямую и точку А, не лежащую на этой прямой. Соединим точку А с точкой Н, лежащей на прямой (Рис.1).

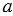
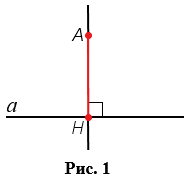
Отрезок АН называется перпендикуляром, проведенным из точки А к прямой 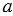, если прямые АН и перпендикулярны.

Содержание

Теорема
Проведение перпендикуляра из точки к прямой
Геометрия. 7 класс
Перпендикулярный треугольник 7 класс
§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника
§ 8. Первый и второй признак равенства треугольников
§ 9. Равнобедренный треугольник и его свойства
§ 10. Признаки равнобедренного треугольника
§ 11. Третий признак равенства треугольников
§ 12. Теоремы
ИТОГИ ГЛАВЫ 2.
🔍 Видео

Видео:Треугольники. 7 класс.Скачать

Теорема

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Доказательство:

1. Существование перпендикуляра.

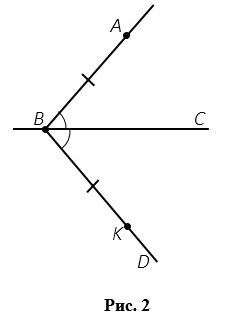
Пусть точка А не лежит на прямой ВС. Проведем луч ВА. Затем от луча ВС отложим угол СВD, равный углу АВС. На луче ВD отложим отрезок ВК, равный отрезку ВА (Рис.2).

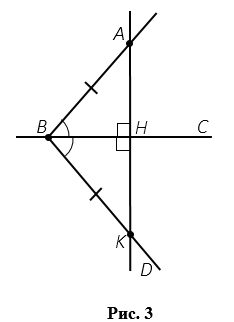
Проведем прямую АК, пусть Н — точка пересечения прямых ВС и АК (Рис.3).

АВН = КВН по первому признаку равенства треугольников: ВН — общая сторона, ВА = ВК, АВН =КBН (по построению), ВНА =ВНD. Но ВНА и ВНD — смежные углы, тогда по свойству смежных углов ВНА +ВНD = 180 0 , следовательно, каждый из смежных улов прямой, т.е. ВНА =ВНD = 90 0 , а значит АНВС.

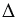
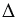
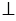
2. Единственность перпендикуляра.

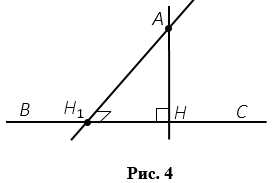
Предположим, что через точку А можно провести еще один перпендикуляр АН₁ к прямой ВС, тогда получим, что две прямые АН и АН₁, перпендикулярные к прямой ВС пересекаются в точке А (Рис.4). Но по свойству перпендикулярных прямых, прямые АН и АН₁ пересекаться не могут, значит, наше предположение неверно и через точку А можно провести только один перпендикуляр к прямой ВС. Теорема доказана.

Видео:Наклонная, проекция, перпендикуляр. 7 класс.Скачать

Проведение перпендикуляра из точки к прямой

Для проведения перпендикуляра из точки к прямой, используют чертежный угольник (Рис.5). Чертежный угольник прикладывают так, чтобы одна из его сторон, образующих прямой угол угольника, располагалась вдоль прямой, к которой нужно провести перпендикуляр. Вдоль второй стороны, образующей прямой угол угольника, проводим прямую так, чтобы она проходила через точку, из которой нужно провести перпендикуляр к прямой. Отрезок, соединяющий точку на прямой, к которой нужно провести перпендикуляр, и точку, из которой нужно провести перпендикуляр, и есть перпендикуляр проведенный из данной точки к данной прямой. На Рис.5 АН.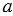

Поделись с друзьями в социальных сетях:

Видео:7 класс, 16 урок, Перпендикуляр к прямойСкачать

Геометрия. 7 класс

Конспект урока

Перпендикуляр к прямой

Перечень рассматриваемых вопросов:

Понятие перпендикуляра к прямой.
Основание перпендикуляра.
Теорема о перпендикуляре к прямой.
Понятие теоремы.
Метод доказательства от противного.

Теорема – утверждение, справедливость которого устанавливается путём рассуждений.

Отрезок – часть прямой, ограниченная двумя точками.

Перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Погорелов А. В. Геометрия: 7–9 класс. // Погорелов А. В. – М.: Просвещение, 2017. – 224 с.

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Пешеходный переход, так называемая «зебра», расположен под углом 90 градусов к улице. Выбор такого угла сделан не случайно. Ведь перейти дорогу пешеходам необходимо как можно быстрее. Такой путь оказывается самым коротким. Чтобы быстрее добраться от метро Площадь Восстания в Санкт-Петербурге до Набережной реки Фонтанки, необходимо идти по Невскому проспекту, перпендикулярно реке.

Ножки стола крепятся перпендикулярно столешнице. Маятник часов расположен перпендикулярно верхней стенке часов.

Если считать улицу, набережную реки Фонтанки, ребро столешницы, ребро стенки часов моделями прямых, то можно говорить, что на каждой картинке построены перпендикуляры к прямой.

Примеры с картой и пешеходным переходом иллюстрируют тот факт, что перпендикуляр к прямой – это кратчайший путь от точки до прямой. Такой путь называется расстоянием.

Пример с часами поможет нам запомнить происхождение слова перпендикуляр. В переводе с французского перпендикуляр означает висеть. То есть, перпендикуляр – это отвес.

Дадим определение перпендикуляра к прямой.

Мы знаем, что перпендикулярными прямыми называются две пересекающиеся прямые, которые образуют при пересечении четыре прямых угла.

Часть одной из этих прямых является перпендикуляром к прямой.

Выделенная часть прямой ограничена двумя точками, значит, по определению, – это отрезок. Один из концов этого отрезка является точкой пересечения перпендикуляра и прямой, к которой он проведен.

перпендикуляр к прямой – это отрезок прямой, перпендикулярной к данной, который имеет одним из своих концов их точку пересечения.

Н – основание перпендикуляра.

Предположим, что вы купаетесь в море недалеко от берега. Вдруг появилась акула, необходимо срочно плыть к берегу. Конечно, вы выберите самый короткий путь. А мы уже знаем, что в геометрии этот путь называют перпендикуляром к прямой.

Всегда ли можно найти кратчайший путь? Сколько существует способов построения кратчайшего пути?

Если на пути нет препятствий, например, здания, ямы, в данном примере – других пловцов, то самый короткий путь проделать можно. И такой путь единственный.

В геометрии любое утверждение требует доказательства. Сформулируем теорему о перпендикуляре к прямой.

Теорема: из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

По условию теоремы нам даны прямая и точка.

Заключение теоремы состоит из двух частей – существование перпендикуляра и его единственность.

1.Через точку А можно провести перпендикуляр к прямой BC.

2.Данный перпендикуляр единственный.

Разбор заданий тренировочного модуля.

Задание 1. Построить перпендикуляр к прямой.

Для этого можно использовать чертёжный угольник, одну сторону которого от угла в 90 градусов прикладываем к прямой, к которой проведём перпендикуляр из точки, не лежащей на этой прямой, а вторую сторону угольника совместим с точкой, от которой проведём перпендикуляр к прямой.

Задание 2. На рисунке изображены два перпендикуляра АB и СD к прямой а, при этом АB = СD.

Докажем, что треугольники ABD и CDВ равны.

По условию в треугольниках ABD и CDВ, сторона АBравна стороне СD.

AB ⊥ а =>∠ABD = 90° (по определению перпендикулярных прямых).

СD ⊥ а => ∠CDВ = 90° (по определению перпендикулярных прямых).

Следовательно, ∠ABD = ∠CDВ.

Сторона BD – общая,

Следовательно, ∆ABD = ∆CDВ

(по первому признаку равенства треугольников: по двум сторонам и углу между ними).

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Перпендикулярный треугольник 7 класс

СОДЕРЖАНИЕ: 7) Равные треугольники. Высота, медиана, биссектриса треугольника. 8) Первый и второй признак равенства треугольников. 9) Равнобедренный треугольник и его свойства. 10) Признаки равнобедренного треугольника. 11) Третий признак равенства треугольников. 12) Теоремы.

§ 7. Равные треугольники. Высота, медиана, биссектриса треугольника

Рассмотрим три точки А, В, С, не лежащие на одной прямой. Соединим их отрезками АВ, ВС, СА. Полученная фигура ограничивает часть плоскости, выделенную на рисунке 108 зеленым цветом. Эту часть плоскости вместе с отрезками АВ, ВС и СА называют треугольником.

Точки А, В, С называют вершинами, а отрезки АВ, ВС, СА — сторонами треугольника. Треугольник называют и обозначают по его вершинам. Треугольник, изображённый на рисунке 108, обозначают так: ΔАВС, или ΔВСА, или ΔАСВ (читают: «треугольник АВС», «треугольник ВСА», «треугольник АСВ»).

Углы ВАС, АВС, ВСА (рис. 109) называют углами треугольника АВС. В треугольнике АВС (рис. 109), например, угол В называют , противолежащим стороне АС, углы А и С — углами, прилежащими к стороне АС, сторону АС — стороной, противолежащей углу В, стороны АВ и АС — сторонами, прилежащими к углу А.

§ 8. Первый и второй признак равенства треугольников

§ 9. Равнобедренный треугольник и его свойства

Определение. Треугольник, у которого две стороны равны, называют равнобедренным.
Равные стороны треугольника называют боковыми сторонами, а третью сторону — основанием равнобедренного треугольника. Вершиной равнобедренного треугольника называют общую точку его боковых сторон. При этом угол В называют углом при вершине, а углы А и С — углами при основании равнобедренного треугольника.

Определение. Треугольник, у которого все стороны равны, называют равносторонним.
Равносторонний треугольник — частный случай равнобедренного треугольника.

§ 10. Признаки равнобедренного треугольника

§ 11. Третий признак равенства треугольников

§ 12. Теоремы

Формулировки всех теорем, которые мы доказали, состоят из двух частей. Первую часть теоремы (то, что дано) называют условием теоремы, вторую часть теоремы (то, что требуется доказать) — заключением.

Например, в теореме 8.1 (первый признак равенства треугольников) условием является то, что две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, а заключением — равенство
ников.

Все знакомые вам теоремы можно условно разделить на теоремы-свойства и теоремы-признаки. Например, теорема 1.1 устанавливает свойство пересекающихся прямых, теорема 9.1 — свойство равнобедренного треугольника.

Теоремы-признаки перечисляют свойства, по которым можно распознать фигуру, т. е. отнести её к тому или иному виду (классу). Так, теоремы-признаки равенства треугольников указывают требования, по которым два треугольника можно причислить к классу равных. Например, в теоремах 10.1-10.4 сформулированы свойства, по которым распознают равнобедренный треугольник.

Теоремы, которые следуют непосредственно из аксиом или теорем, называют теоремами-следствиями или следствиями. Например, свойство углов, противолежащих равным сторонам треугольника, является следствием из теоремы 9.1.
Если в теореме 8.2 о свойстве серединного перпендикуляра поменять местами условие и заключение, то получим теорему 11.2. Такие теоремы называют взаимно обратными. Если какую-то из этих теорем назвать прямой, то вторую теорему будем называть обратной.

Меняя местами условие и заключение теоремы, надо быть очень внимательными: не всегда можно получить истинное утверждение. Например, утверждение, обратное теореме 4.1 о сумме смежных углов, неверно. Действительно, если сумма каких-то двух углов равна 180°, то совершенно не обязательно, чтобы эти углы были смежными.

Вы знаете, что справедливость теоремы устанавливают путём логических рассуждений, т. е. доказательства. Теорема 1.1 была доказана методом от противного. Название этого метода фактически отражает его суть. Мы предположили, что заключение теоремы 1.1 неверно. На основании этого предположения с помощью логических рассуждений был получен факт, который противоречил основному свойству прямой.

Методом от противного также были доказаны и другие теоремы, например теоремы 5.1, 10.3. Очень важно, чтобы доказательство теоремы было полным, т. е. рассмотрены все возможные случаи. Так, полное доказательство теоремы 11.1 (третий признак равенства треугольников) потребовало рассмотрения всех трёх возможных случаев.

Умение видеть все тонкости и нюансы доказательства — важнейшее качество, формирующее математическую культуру. Если бы, например, при доказательстве теоремы 8.2 о свойстве серединного перпендикуляра мы не рассмотрели отдельно случай, когда точка X является серединой отрезка то обращение к треугольникам АХМ и ВХМ было бы не совсем «законным».

При доказательстве теоремы 10.4 (признак равнобедренного треугольника) мы использовали приём дополнительного построения: чертёж дополнили элементами, о которых не шла речь в условии теоремы. Этот метод является ключом к решению многих задач и доказательству ряда теорем. Поэтому очень важно научиться видеть «выгодное» (результативное) дополнительное построение.

ИТОГИ ГЛАВЫ 2.

Определение. Равные фигуры
Две фигуры называют равными, если их можно совместить наложением.

Основное свойство равенства треугольников
Для данного треугольника АВС и луча А₁М существует треугольник A₁B₁C₁ равный треугольнику АВС, такой, что АВ = А₁В₁, ВС = В₁С₁, АС = А₁С₁ и сторона A₁B₁ принадлежит лучу А₁М, а вершина С₁ лежит в заданной полуплоскости относительно прямой А₁М.

ТЕОРЕМА 7.1. О единственности прямой, перпендикулярной данной
Через точку, не принадлежащую данной прямой, проходит только одна прямая, перпендикулярная данной.

Высота треугольника
Перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону, называют высотой треугольника.

Медиана треугольника
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называют медианой треугольника.

Биссектриса треугольника
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называют биссектрисой треугольника.

ТЕОРЕМА 8.1. Первый признак равенства треугольников: по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Серединный перпендикуляр отрезка
Прямую, перпендикулярную отрезку и проходящую через его середину, называют серединным перпендикуляром отрезка.

ТЕОРЕМА 8.2.
Каждая точка серединного перпендикуляра отрезка равноудалена от концов этого отрезка.

ТЕОРЕМА 8.3. Второй признак равенства треугольников: по стороне и двум прилежащим к ней углам
Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Равнобедренный треугольник
Треугольник, у которого две стороны равны, называют равнобедренным.

Равносторонний треугольник
Треугольник, у которого все стороны равны, называют равносторонним.

ТЕОРЕМА 9.1. Свойства равнобедренного треугольника
В равнобедренном треугольнике: 1) углы при основании равны; 2) биссектриса треугольника, проведённая из угла при вершине, является медианой и высотой.

Свойства треугольников, следующие из свойств равнобедренного треугольника
• В треугольнике против равных сторон лежат равные углы.
• В равнобедренном треугольнике биссектриса, высота и медиана, проведённые из его вершины, совпадают.
• В равностороннем треугольнике все углы равны.
• В равностороннем треугольнике биссектриса, высота и медиана, проведённые из одной вершины, совпадают.

Признаки равнобедренного треугольника
• Если медиана треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.1)
• Если биссектриса треугольника является его высотой, то этот треугольник равнобедренный (Теорема 10.2)
• Если в треугольнике два угла равны, то этот треугольник равнобедренный (Теорема 10.3)
• Если медиана треугольника является его биссектрисой, то этот треугольник равнобедренный (Теорема 10.4)

ТЕОРЕМА 11.1.Третий признак равенства треугольников: по трём сторонам
Если три стороны одного треугольника равны соответственно трём сторонам другого треугольника, то такие треугольники равны.

Это конспект по теме «Мерзляк Геометрия 7 Глава 2». Выберите дальнейшие действия: