- Primary tabs
- Forums:
- Скалярное произведение комплексных векторов
- Норма вектора через скалярное произведение
- Косинус угла через скалярное произведение и норму
- Пример расчета косинуса для комплексных векторов
- Вычисление угла между комплексными векторами
- Угол вектора комплексного числа
- Комплексные числа и операции с ними
- Комплексные числа
- Алгебраическая форма записи комплексных чисел
- Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
- Комплексно сопряженные числа
- Модуль комплексного числа
- Деление комплексных чисел, записанных в алгебраической форме
- Изображение комплексных чисел радиус-векторами координатной плоскости
- Аргумент комплексного числа
- Формула Эйлера. Экспоненциальная форма записи комплексного числа
- Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
- Извлечение корня натуральной степени из комплексного числа
- Аргумент и модуль комплексного числа
- Как найти угол вектора комплексного числа
Видео:Изображение комплексных чисел. Модуль комплексного числа. 11 класс.Скачать

Primary tabs
Forums:
Видео:Аргумент комплексного числа. Часть 1Скачать

Скалярное произведение комплексных векторов
Видео:2. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числаСкачать

Норма вектора через скалярное произведение
Евклидова норма через скалярное произведение для вектора $x$ выглядит так:
$Large ||x|| = sqrt$
Видео:Найти модуль и аргумент комплексного числа #maths #complexnumbers #complexanalysis #тфкп #calculusСкачать

Косинус угла через скалярное произведение и норму
Косинус угла $m$ между векторами $x$ и $y$ в комплексном пространстве определяется равенством:
$Large cos , m = <(x, y)over>$
где:
- $(x,y)$ — скалярное произведение этих векторов
- а $||x|| * ||y||$ — произведение их норм
Видео:10 класс, 34 урок, Тригонометрическая форма записи комплексного числаСкачать

Пример расчета косинуса для комплексных векторов
Возьмём два вектора:
$[1+i, 2]$ и $[2+i, i]$
Вычислим:
- Их скалярное произведение: $ [1+i, 2] cdot [2+i, i] = (1+i) cdot (overline) + 2 cdot overline i = (1+i) cdot (2-i) + 2 cdot (-i) = 3-i$
- Норму $[1+i, 2]$:
$sqrt = sqrt = sqrt$ - Норму $[2+i, i]$:
$sqrt = sqrt = sqrt$
Тогда для косинуса угла между этими векторами получаем:
$large cos , m = <3 — i over<sqrt* sqrt>> = <3 — i over>$
т.е. фактически комплексное число (т.е. комплексное значение косинуса).
Видео:КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Вычисление угла между комплексными векторами
Вычисление угла требует получения арккосинуса для комплексного числа.
Видео:Математика без Ху!ни. Комплексные числа, часть 3. Формы записи. Возведение в степень.Скачать

Угол вектора комплексного числа
Видео:Тригонометрическая форма комплексного числаСкачать

Комплексные числа и операции с ними
DSPL-2.0 — свободная библиотека алгоритмов цифровой обработки сигналов
Распространяется под лицензией LGPL v3
Известно, что область определения некоторых функций на множестве вещественных чисел ограничена. Например функция определена для , аналогично можно вспомнить, что функция определена для 0″/>, а функция определена для .
Однако, ограниченная область определения функций на множестве вещественных чисел не означает, что , или не имеют смысла. Ограниченная область определения функций на множестве вещественных чисел говорит лишь о том, что не может быть представлено вещественным числом. Действительно, среди вещественных чисел не найти такого числа , квадрат которого был бы равен .
При решении квадратных уравнений часто возникает ситуация, когда дискриминант отрицательный. В этом случае это означает что парабола не пересекает прямую абсцисс ни в одной точке. Другими словами, корни квадратного уравнения не существуют среди вещественных значений и их также надо искать за пределами вещественных чисел.
Все бесконечное множество вещественных чисел можно представить в виде одной числовой прямой (смотри рисунок 1), на которой мы можем откладывать рациональные и иррациональные вещественные числа. Но на этой прямой нет числа , значит его надо искать вне числовой прямой. Таким образом мы должны расширить множество вещественных чисел до множества в котором значения , или уже не бессмысленны, а являются такими же обычными числами в этом расширенном множестве, как на множестве вещественных чисел.
Естественным расширением числовой прямой является плоскость, которую называют комплексной плоскостью. Числовая прямая вещественных чисел и ее расширение до комплексной плоскости показано на рисунке 1. Любая точка на комплексной плоскости определяет одно комплексное число. Например на рисунке 1 показано число .
Значение вещественного числа однозначно определяет его позицию на числовой прямой, однако для определения позиции на плоскости одного числа недостаточно.
Для «навигации» по комплексной плоскости вводятся две прямые и , которые пересекаются в начале координат. Прямая это числовая прямая, называемая реальной осью, на которой лежат все вещественные числа. Прямая называется мнимой осью и она перпендикулярна реальной оси . Оси и делят комплексную плоскость на четверти, как это показано на рисунке 1.
Любая точка комплексной плоскости задается двумя координатами и по осям и соответственно. При этом само комплексное число можно записать как , где называется реальной частью и задает координату точки комплексной плоскости на вещественной прямой , а называется мнимой частью и задает координату точки комплексной плоскости на мнимой оси .
Для того чтобы отделить одну координату от другой (реальную и мнимую части) вводят число , называемое мнимой единицей. Это так раз то число, которого не существует на множестве действительных чисел. Оно обладает особым свойством: . Тогда комплексное число может не только перемещаться по вещественной прямой вправо и влево, но и двигаться по комплексной плоскости потому что мы добавили ему слагаемое с мнимой единицей .
Мнимую единицу в математической литературе принято обозначать как , но в технике буква уже закреплена за обозначением электрического тока, поэтому чтобы избежать путаницы мы будем обозначать мнимую единицу буквой .
Если и , тогда число является действительным и располагается на реальной оси .
Если и , тогда число является чисто мнимым и располагается на мнимой оси .
Если и , тогда число располагается в одной из четвертей комплексной плоскости.
Представление комплексного числа как называют алгебраической формой записи. Если из начала координат комплексной плоскости к точке восстановить вектор (смотри рисунок 1), то можно вычислить длину этого вектора как
Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:
Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Комплексные числа
 Алгебраическая форма записи комплексных чисел Алгебраическая форма записи комплексных чисел |
 Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме |
 Комплексно сопряженные числа Комплексно сопряженные числа |
 Модуль комплексного числа Модуль комплексного числа |
 Деление комплексных чисел, записанных в алгебраической форме Деление комплексных чисел, записанных в алгебраической форме |
 Изображение комплексных чисел радиус-векторами на координатной плоскости Изображение комплексных чисел радиус-векторами на координатной плоскости |
 Аргумент комплексного числа Аргумент комплексного числа |
 Тригонометрическая форма записи комплексного числа Тригонометрическая форма записи комплексного числа |
 Формула Эйлера. Экспоненциальная форма записи комплексного числа Формула Эйлера. Экспоненциальная форма записи комплексного числа |
 Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме |
 Извлечение корня натуральной степени из комплексного числа Извлечение корня натуральной степени из комплексного числа |
Видео:Угол между векторами. 9 класс.Скачать

Алгебраическая форма записи комплексных чисел
Пусть x и y — произвольные вещественные числа.
Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.
Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0) .
Комплексные числа, заданные парами (0, y) , называют чисто мнимыми числами .
Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи .
Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число z, заданное парой вещественных чисел (x, y) , записывается в виде
| z = x + i y . | (1) |
где использован символ i , называемый мнимой единицей .
Число x называют вещественной (реальной) частью комплексного числа z = x + i y и обозначают Re z .
Число y называют мнимой частью комплексного числа z = x + i y и обозначают Im z .
Комплексные числа, у которых Im z = 0 , являются вещественными числами .
Комплексные числа, у которых Re z = 0 , являются чисто мнимыми числами .
Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.
Видео:Математика без Ху!ни. Угол между векторами, применение скалярного произведения.Скачать

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме
Умножение комплексных чисел z1 = x1 + i y1 и z2 = x2 + i y2 , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:
| i 2 = – 1 . | (2) |
По этой причине
Видео:Угол между векторами | МатематикаСкачать

Комплексно сопряженные числа
Два комплексных числа z = x + iy и 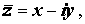
Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения , обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:
 |  |
 |  |
 |  |
 |  |
 |  |
Видео:Аргумент комплексного числаСкачать

Модуль комплексного числа
Модулем комплексного числа z = x + i y называют вещественное число, обозначаемое | z | и определенное по формуле
Для произвольного комплексного числа z справедливо равенство:
а для произвольных комплексных чисел z1 и z2 справедливы неравенства:
 |  |
 |  |
 |  |
 |  |
Замечание . Если z — вещественное число, то его модуль | z | равен его абсолютной величине.
Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Деление комплексных чисел, записанных в алгебраической форме
Деление комплексного числа z1 = x1 + i y1 на отличное от нуля комплексное число z2 = x2 + i y2 осуществляется по формуле
Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:
Деление на нуль запрещено.
Видео:Комплексные числа. Тригонометрическая форма. Формула Муавра | Ботай со мной #040 | Борис Трушин !Скачать

Изображение комплексных чисел радиус-векторами координатной плоскости
Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат Oxy и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.
Назовем рассматриваемую плоскость комплексной плоскостью , и будем представлять комплексное число z = x + i y радиус–вектором с координатами (x , y).
Назовем ось абсцисс Ox вещественной осью , а ось ординат Oy – мнимой осью .
При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.
Видео:Как находить угол между векторамиСкачать

Аргумент комплексного числа
Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа z .
Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором z .
Аргумент комплексного числа z считают положительным, если поворот от положительного направления вещественной оси к радиус-вектору z происходит против часовой стрелки, и отрицательным — в случае поворота по часовой стрелке (см. рис.).
Считается, что комплексное число нуль аргумента не имеет.
Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где k — произвольное целое число, то вводится, главное значение аргумента , обозначаемое arg z и удовлетворяющее неравенствам:
Тогда оказывается справедливым равенство:
Если для комплексного числа z = x + i y нам известны его модуль r = | z | и его аргумент φ , то мы можем найти вещественную и мнимую части по формулам
 | (3) |
Если же комплексное число z = x + i y задано в алгебраической форме, т.е. нам известны числа x и y , то модуль этого числа, конечно же, определяется по формуле
 | (4) |
а аргумент определяется в соответствии со следующей Таблицей 1.
Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом k обозначать в Таблице 1 произвольное целое число.
Таблица 1. – Формулы для определения аргумента числа z = x + i y
| Расположение числа z | Знаки x и y | Главное значение аргумента | Аргумент | Примеры |
| Положительная вещественная полуось | 0 | φ = 2kπ |  | |
| Первый квадрант |  |  |  | |
| Положительная мнимая полуось |  |  |  | |
| Второй квадрант |  |  |  | |
| Отрицательная вещественная полуось | Положительная вещественная полуось | |||
| Знаки x и y | ||||
| Главное значение аргумента | 0 | |||
| Аргумент | φ = 2kπ | |||
| Примеры |  |
| Расположение числа z | Первый квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Положительная мнимая полуось |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Второй квадрант |
| Знаки x и y | |
| Главное значение аргумента |  |
| Аргумент |  |
| Примеры |  |
| Расположение числа z | Отрицательная вещественная полуось |
| Знаки x и y | Третий квадрант |
| Знаки x и y | Отрицательная мнимая полуось |
| Знаки x и y | Четвёртый квадрант |
| Знаки x и y |
| z = r (cos φ + i sin φ) , | (5) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа .
Видео:ТФКП. Найти модуль и аргумент комплексных чисел. Функции комплексного переменного. Значение функции.Скачать

Формула Эйлера. Экспоненциальная форма записи комплексного числа
В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера :
| cos φ + i sin φ = e iφ . | (6) |
Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число z = x + i y может быть записано в виде
| z = r e iφ , | (7) |
где r и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству r > 0 .
Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа .
Из формулы (7) вытекают, в частности, следующие равенства:
а из формул (4) и (6) следует, что модуль комплексного числа
или, что то же самое, числа e iφ , при любом значении φ равен 1.
Видео:ТФКП. Как найти все значения корня из комплексного числаСкачать

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме
Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.
Действительно, умножение и деление двух произвольных комплексных чисел 

Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.
При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.
Возведение комплексного числа z = r e iφ в натуральную степень осуществляется по формуле
Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.
Видео:Формула Муавра. Возведение комплексного числа в степеньСкачать

Извлечение корня натуральной степени из комплексного числа
Пусть 
Корнем n — ой степени из числа z0 , где 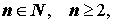
| z n = z0 . | (8) |
Для того, чтобы решить уравнение (8), перепишем его в виде
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна 2kπ , где k — произвольное целое число. По этой причине справедливы равенства
следствием которых являются равенства
 | (9) |
Из формул (9) вытекает, что уравнение (8) имеет n различных корней
 | (10) |
причем на комплексной плоскости концы радиус-векторов zk при k = 0 , . , n – 1 располагаются в вершинах правильного n — угольника, вписанного в окружность радиуса 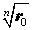
Замечание . В случае n = 2 уравнение (8) имеет два различных корня z1 и z2 , отличающихся знаком:
Пример 1 . Найти все корни уравнения
то по формуле (10) получаем:
Пример 2 . Решить уравнение
Решение . Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:
Видео:Математика без Ху!ни. Комплексные числа, часть 1. Введение.Скачать

Аргумент и модуль комплексного числа
Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Из определения следуют следующие формулы:
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 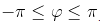
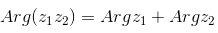 | — аргумент от произведения двух комплексных чисел равен сумме аргументов этих чисел |
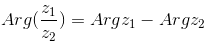 | — аргумент частного двух комплексных чисел равен разности аргументов этих чисел |
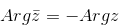 | — аргумент от сопряженного комплексного числа равен отрицательному значению аргумента от этого числа. |
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
Как найти угол вектора комплексного числа
Комплексным числом называется выражение вида z = x + iy , (7.1)
где x и y – действительные числа, а i так называемая мнимая единица. Соотношение для мнимой единицы
Если x =0, то число 0+ iy = iy называется чисто мнимым; если y =0, то число x + i ∙0= x отождествляется с действительным числом x , а это означает, что множество R всех действительных чисел является подмножеством множества C всех комплексных чисел, то есть 
Число x называется действительной частью комплексного числа z и обозначается x = Re z , а y – мнимой частью комплексного числа z и обозначается y = Im z .
Понятия «больше» и «меньше» для комплексных чисел не вводятся.
Числа z = x + iy и 
Всякое комплексное число z = x + iy можно изобразить точкой M ( x ; y ) плоскости x 0 y такой, что x = Re z , y = Im z . Верно и обратное: каждую точку M ( x ; y ) координатной плоскости можно рассматривать как образ комплексного числа z = x + iy (рис. 7.1).
Комплексное число z = x + iy можно задавать с помощью радиус-вектора 


Для комплексного числа z =0 аргумент не определен. Аргумент комплексного числа 

Алгебраической формой комплексного числа называется з апись числа z в виде z = x + iy.
Модуль r и аргумент φ можно рассматривать как полярные координаты вектора 
Равенство (7.3) есть тригонометрическая форма комплексного числа. Модуль r = |z| однозначно определяется по формуле
Аргумент определяется из формул:
При переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить главное значение аргумента комплексного числа z , то есть считать φ= arg z . Знаки полученных значений cos φ и sin φ по формулам (7.5), дают возможность определить, какой координатной четверти принадлежит угол φ.
Используя формулу Эйлера
комплексное число 
где r =| z | — модуль комплексного числа, а угол 
Функция e i φ – периодическая с основным периодом 2 π, поэтому для записи комплексного числа в показательной форме по формуле 7.7 достаточно найти главное значение его аргумента, то есть считать φ = arg z .
Пример 7.1. Записать комплексные числа 
Решение. Для z 1 имеем 

Для действительного числа 
На множестве комплексны х чисел определен ряд операций.
Из равенства (7.9) следует, что геометрически комплексные числа вычитаются как векторы. При этом число z = z 1 – z 2 изображается вектором, соединяющим концы векторов 


Из (7.11) следует важнейшее соотношение i 2 = –1. Действительно,
Найдем произведение комплексных чисел 

Видно, что при умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются. Это правило распространяется на любое конечное число множителей. Нетрудно видеть, что если есть n множителей и все они одинаковые, то частным случаем равенства (7.12) является формула возведения комплексного числа в натуральную степень:
(7.13) называется первой формулой Муавра.
Произведение двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
4. Частным двух комплексных чисел z 1 и 


Пусть 
На практике при нахождении частного двух комплексных чисел удобно умножить числитель и знаменатель дроби 
Деление комплексных чисел осуществляется также и в тригонометрической форме, при этом имеет место формула:
Видно, что при делении комплексных чисел их модули делятся, а аргументы вычитаются соответственно.
Частное двух комплексных чисел в показательной (экспоненциальной) форме имеет вид:
Пример 7.2. Найти сумму, разность, произведение и частное комплексных чисел 
Решение. По формуле (7.8) сумма заданных чисел равна 
Согласно формуле (7.9) разность заданных чисел равна 
Пользуясь формулой (7.11), вычислим их произведение
На основании формулы (7.14) вычислим их частное
Пример 7.3. Найти произведение и частное комплексных чисел 
Решение. Используя (7.4) и (7.5), получаем:
Аналогично, для z 2 можно записать:
По формулам (7.12) и (7.16) получим в тригонометрической форме:
Пользуясь формулами (7.14) и (7.17), получим в показательной форме:
5. Извлечение корня n -ой степени – операция, обратная возведению
в натуральную степень, определенному ранее формулой (7.13).
Корнем n -ой степени из комплексного числа z называется комплексное число ω, удовлетворяющее равенству ω n = z , то есть 
Пусть 



(7.18) называется второй формулой Муавра.
Видно, что для любого 
Пример 7.4. Найти все корни уравнения z 4 +16=0.
Решение. Запишем уравнение в виде z 4 =–16+0∙ i . Отсюда по формуле (7.18) получим:
Сформулируем несколько иначе основную теорему алгебры 3.2 над полем комплексных чисел .
Теорема 7.1 (основная теорема алгебры). Для всякого многочлена с комплексными коэффициентами
Приведем еще одну теорему, имеющую место над множеством комплексных чисел.
Теорема 7.2. Если многочлен Pn ( x ) с действительными коэффициентами имеет комплексный корень a + ib , то он имеет и сопряженный корень a – ib
В разложение многочлена 

Таким образом, произведение линейных множителей, соответствующих сопряженным корням, можно заменить квадратным трехчленом с действительными коэффициентами, а соответствующее квадратное уравнение будет иметь отрицательный дискриминант.