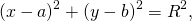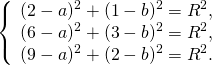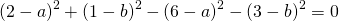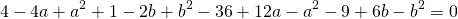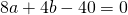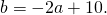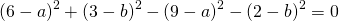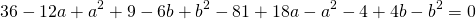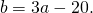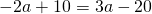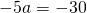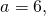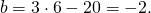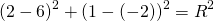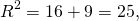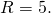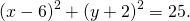Как найти центр описанной окружности треугольника векторы (6 видео)

Уравнение описанной окружности

Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?

Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.

Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).

Подставив координаты вершин треугольника в уравнение окружности

получим систему уравнений

Вычтем из первого уравнения системы второе:

Теперь из второго уравнения системы вычтем третье:

Приравняем правые части равенств b=-2a+10 и b=3a-20:

Подставим в первое уравнение системы a=6 и b=-2:

a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности

Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.

Содержание

Центр описанной окружности треугольника
Окружность, описанная около треугольника
Определение окружности, описанной около треугольника
Теорема об окружности, описанной около треугольника
🎦 Видео

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Центр описанной окружности треугольника

Если треугольник вписан в окружность так, что его вершины располагаются на окружности, такая окружность называется описанной, а треугольник считается вписанным в данную окружность.

Центр окружности расположен в точке пересечения серединных перпендикуляров, проведенных к сторонам треугольника. Серединный перпендикуляр — прямая, которая проходит через середину отрезка, перпендикулярно ему.
Вокруг треугольника возможно описать только одну окружность.

Чтобы определить радиус R описанной окружности, необходимо произведение сторон треугольника (a × b × с) разделить на учетверенную S — площадь треугольника:
R = (a × b × с) / 4S.

Если окружность описана около равностороннего треугольника, радиус R равняется:
R = a /√3.

В том случае, когда окружность описана около прямоугольного треугольника, середина его гипотенузы (с ) является центром описанной окружности.
Радиус R составляет ½ гипотенузы: R = с/2.

Радиус окружности R также равняется медиане m, проведенной к гипотенузе: R = m.

Воспользовавшись онлайн калькулятором, вы сможете быстро и правильно определить координаты центра описанной окружности.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность, описанная около треугольника

Видео:Радиус описанной окружностиСкачать

Определение окружности, описанной около треугольника

Определение 1. Окружностью, описанной около треугольника называется окружность, проходящей через все три вершины треугольника (Рис.1).

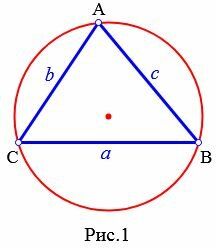Как найти центр описанной окружности треугольника векторы

При этом треугольник называется треугольником вписанным в окружность .

Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать

Теорема об окружности, описанной около треугольника

Теорема 1. Около любого треугольника можно описать окружность.

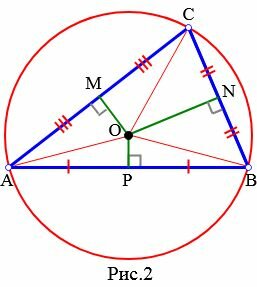Доказательство. Пусть задан произвольный треугольник ABC (Рис.2). Обозначим точкой O точку пересечения серединных перпендикуляров к его сторонам. Проведем отрезки OA, OB и OC. Поскольку точка O равноудалена от точек A, B и C, то OA=OB=OC. Тогда окружность с центром O и радиусом OA проходит через все три вершины треугольника ABC и, следовательно, является окружностью, описанной около треугольника ABC.

Из теоремы 1 следует, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника.

Замечание 1. Около любого треугольника можно описать только одну окружность.

Доказательство. Допустим, что около треугольника можно описать две окружности. Тогда центр каждой из этих окружностей равноудален от вершин треугольника и совпадает с точкой O пересечения серединных перпендикуляров сторон треугольника. Радиус этих окружностей равен расстоянию от точки O до вершин треугольника. Поэтому эти окружности совпадают.