Как найти сторону окружности формула

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Определение стороны окружности

Сторона окружности — это длина дуги окружности.

Длина дуги численно равна стороне
окружности, поэтому более распространено
понятие дуги окружности.

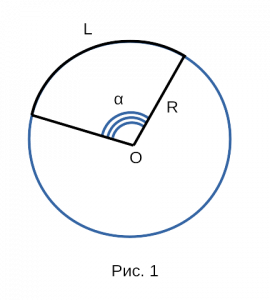
На рисунке 1, изображена окружность,
обладающая следующими величинами:

• O — точка, являющаяся
  центром окружности;
• R — радиус
  окружности;
• α — центральный
  угол окружности;
• L — сторона
  окружности;

Длину стороны L, окружности,
с центром в точке O, можно
найти следующим образом:

Ⅰ. Умножить радиус окружности на π,
получившееся разделить на 180 градусов.
Ⅱ. Полученный результат умножить на угол.

Также, все это можно сделать, зная одну из
известных формул стороны окружности:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Формулы стороны окружности

Ⅰ. Через диаметр и центральный угол

Сторону окружности L, можно найти, разделив
произведение половины диаметра и π на 180 градусов.
Затем умножить полученное значение на угол.

Ⅱ. Через площадь и центральный угол

Эта формула, примечательна тем, что
для нахождения длины, не обязательно
знать радиус — главное знать площадь.

Ⅲ. Через периметр и центральный угол

Самая краткая запись формулы
стороны окружности.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Пример решения задач по теме сторона окружности

Возьмем для удобства π равное 3.14.

Ⅰ.
Дано: Диаметр равен 6, центральный равен 180.
Найти: Длина стороны окружности — ?

Решение:

( L = frac<frac cdot pi> cdot 180 = frac cdot 180 = 3pi = 9.42 )

Ⅱ.
Дано: Периметр равен 100, центральный угол равен 60.
Найти: Длина стороны окружности — ?

Решение:

( L = frac cdot 60 = 0.55 cdot 60 = 33 )

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Калькулятор расчета стороны правильного многоугольника через радиусы окружностей

В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Расчет длины стороны

Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Длина окружности

О чем эта статья:

6 класс, 9 класс, ЕГЭ/ОГЭ

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Длина окружности. Математика 6 класс.Скачать

Как найти длину окружности через диаметр

Хорда — это отрезок, который соединяет две точки окружности.

Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, примерно равное 3,14

r — радиус окружности

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14

S — площадь круга

Видео:Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, примерно равное 3,14

d — диагональ прямоугольника

Видео:ЕГЭ 6 номер. Нахождение стороны правильного треугольника по радиусу вписанной окружности.Скачать

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

π — математическая константа, примерно равная 3,14

a — сторона квадрата

Видео:Радиус описанной окружностиСкачать

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Видео:Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Видео:Как найти сторону квадрата в который вписаны 2 окружностиСкачать

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Обучение на курсах по математике поможет закрепить полученные знания на практике.

🔍 Видео

+Как найти длину окружностиСкачать

112. Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписаннойСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Формулы равностороннего треугольника #shortsСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать