Как найти собственный вектор матрицы в экселе

Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:

• умножение и деление матрицы на число;
• сложение, вычитание и умножение матриц;
• транспонирование матрицы;
• нахождение обратной матрицы;
• вычисление определителя.

Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, а_ij — элемент матрицы.

Видео:Собственные значения и собственные векторы матрицы (4)Скачать

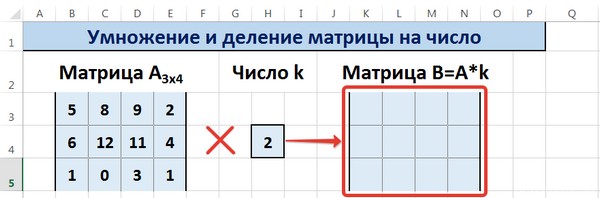
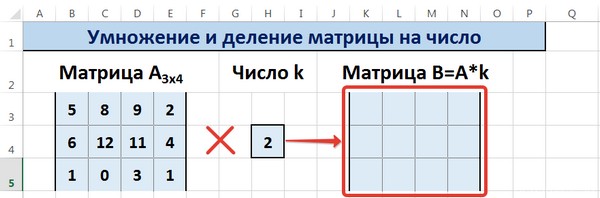
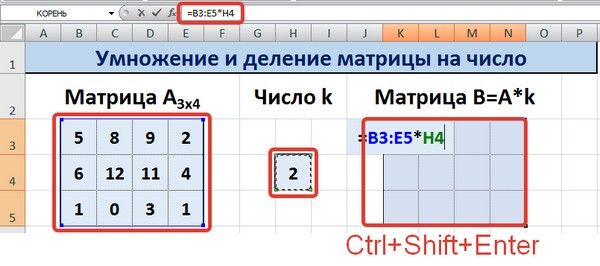
Умножение и деление матрицы на число в Excel

Способ 1

Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.

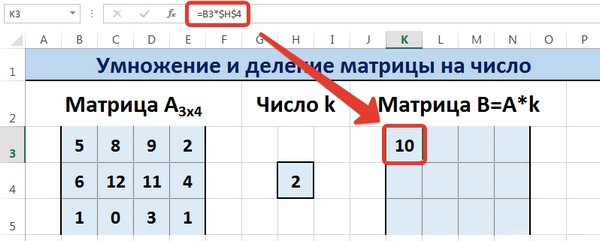
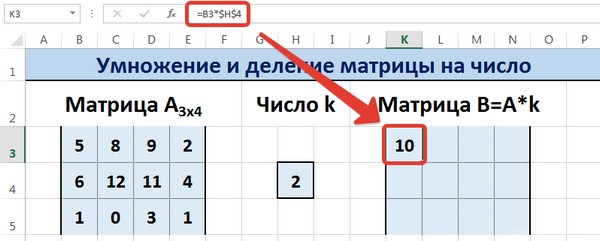
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а₁₁ матрицы А.

Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.

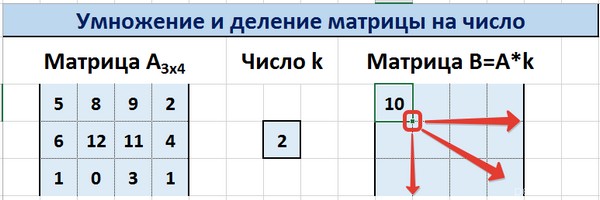
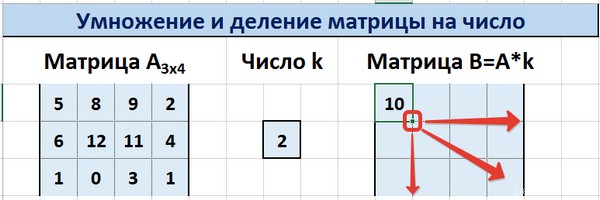
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.

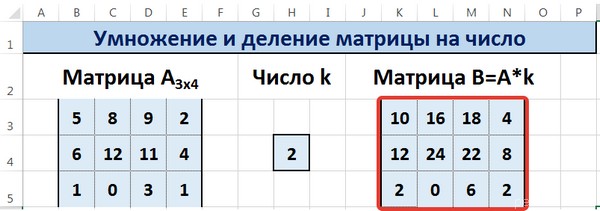
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.

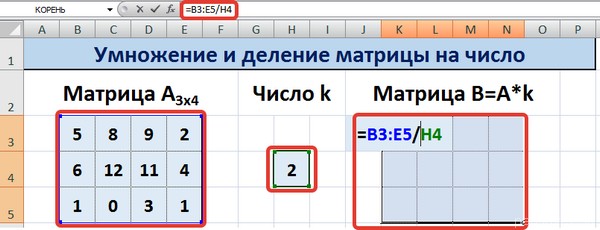
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.

Способ 2

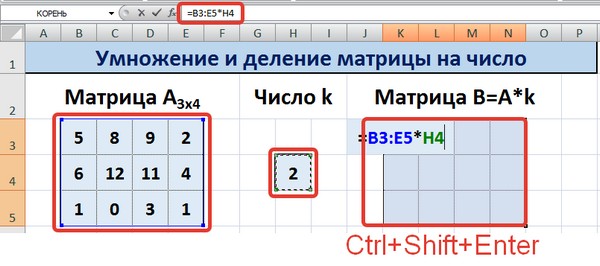
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.

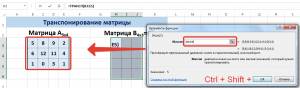
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».

Видео:Собственные векторы и собственные числа линейного оператораСкачать

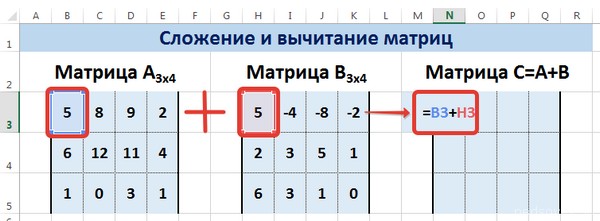
Сложение и вычитание матриц в Excel

Способ 1

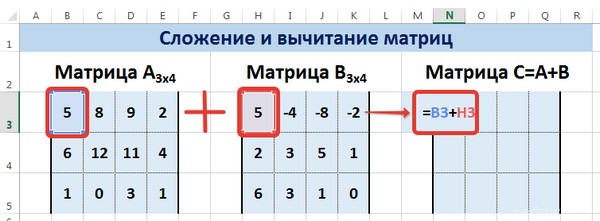
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. с_ij = а_ij + b_ij.

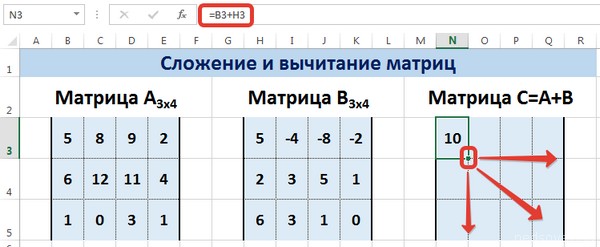
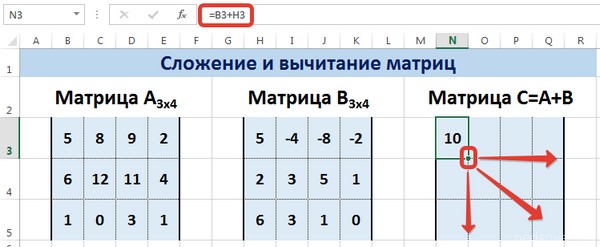
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.

С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.

Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.

Способ 2

Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.

Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.

Видео:Как найти обратную матрицу в экселеСкачать

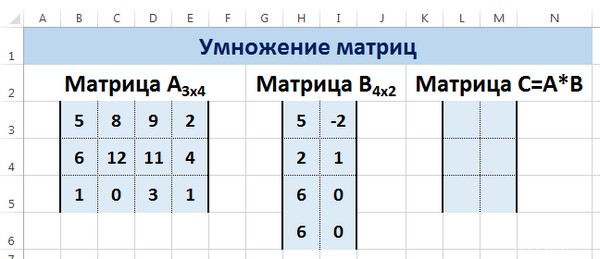
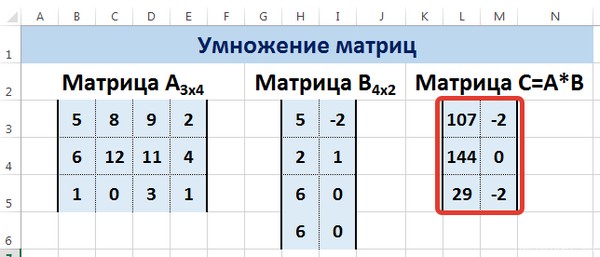
Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

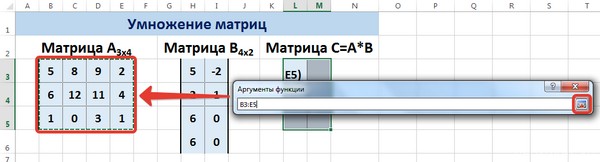
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

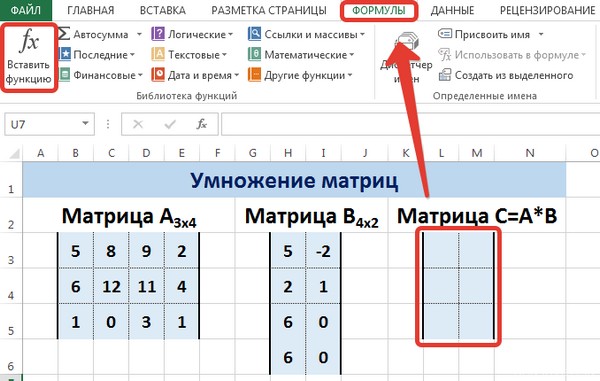
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

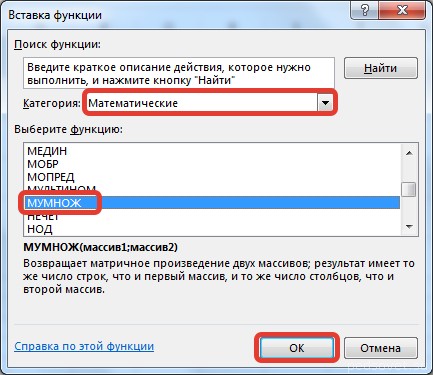
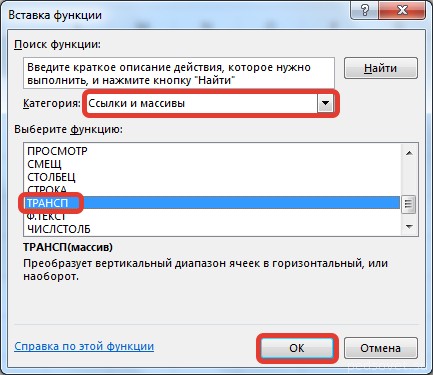
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

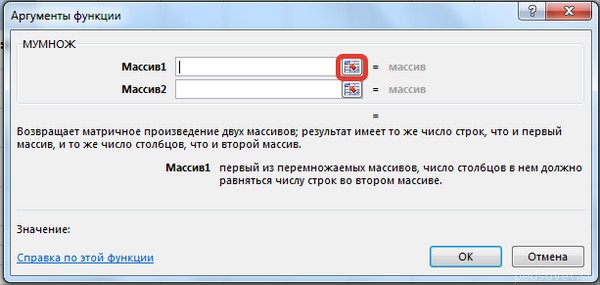
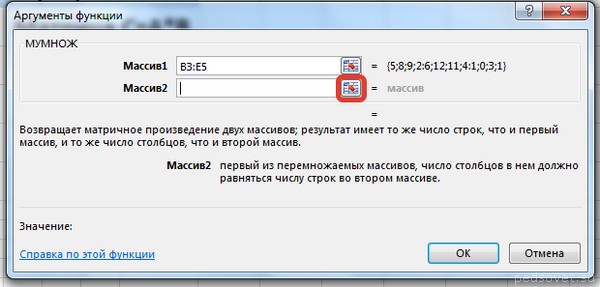
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

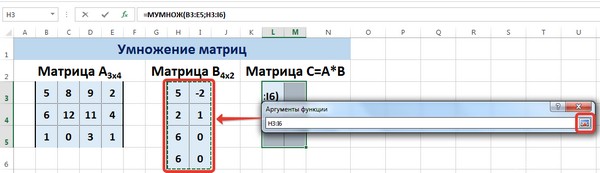
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

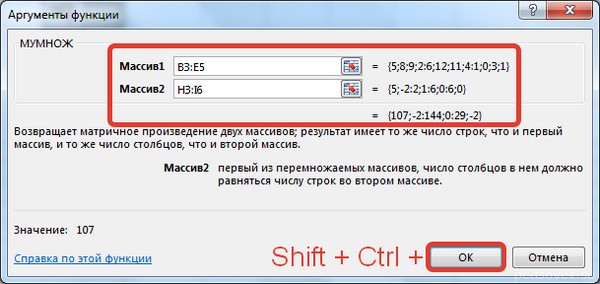
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

Видео:Действия с матрицами в ExcelСкачать

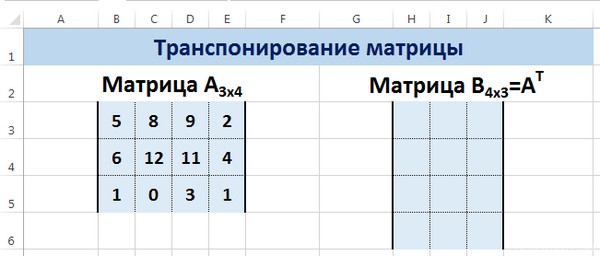
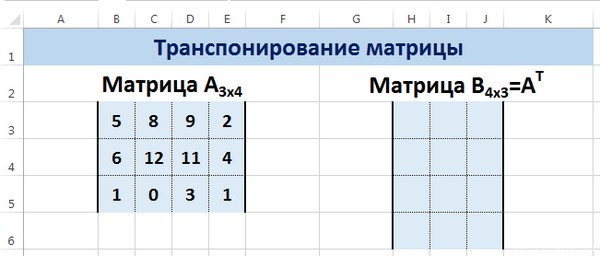
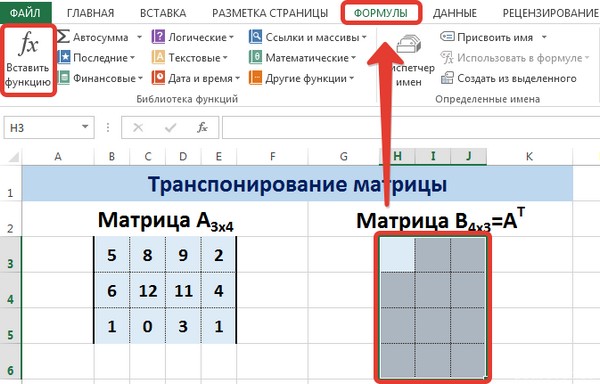
Транспонирование матрицы в Excel

Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .

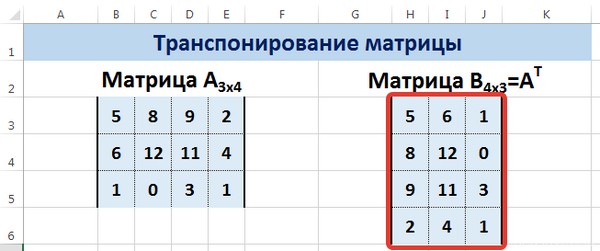
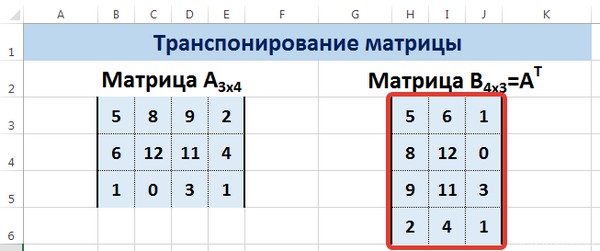
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.

Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.

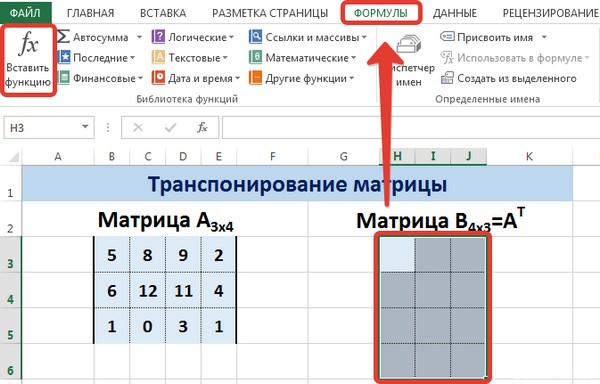
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.

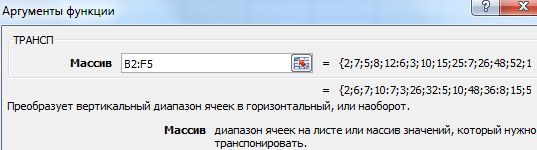
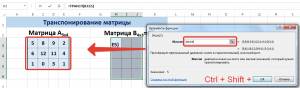
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения

Мы получили транспонированную матрицу.

Видео:Собственные значения и собственные векторыСкачать

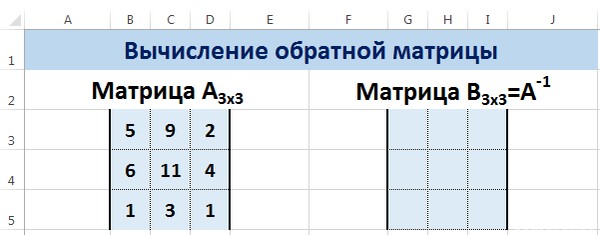
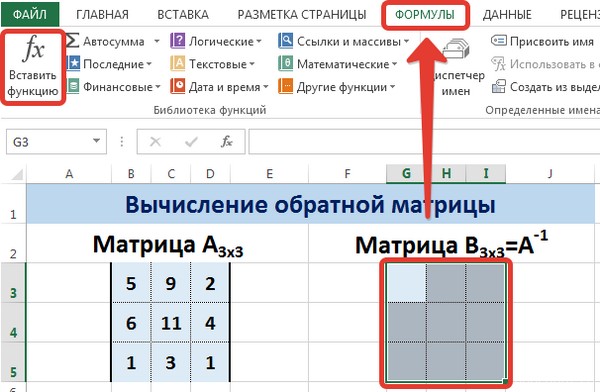
Нахождение обратной матрицы в Excel

Матрица А -1 называется обратной для матрицы А, если АžА -1 =А -1 žА=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).

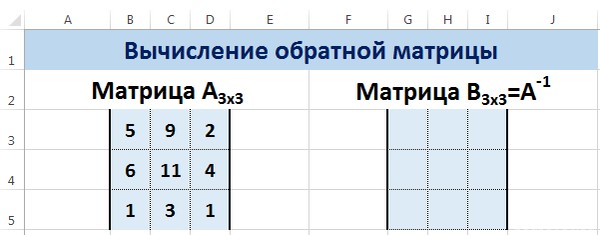
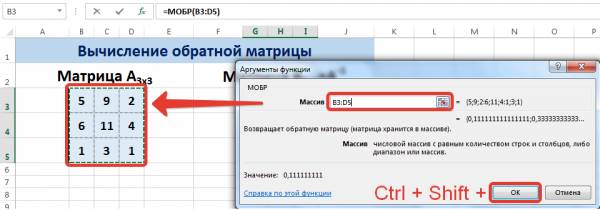
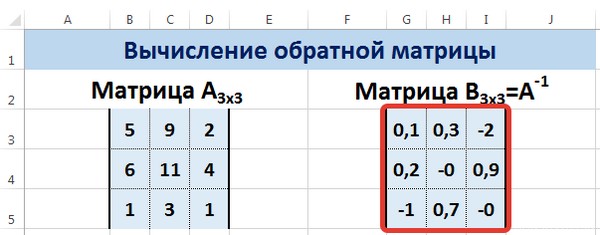
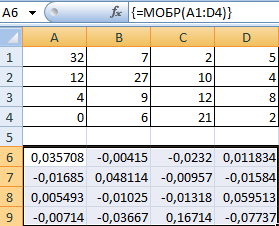
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().

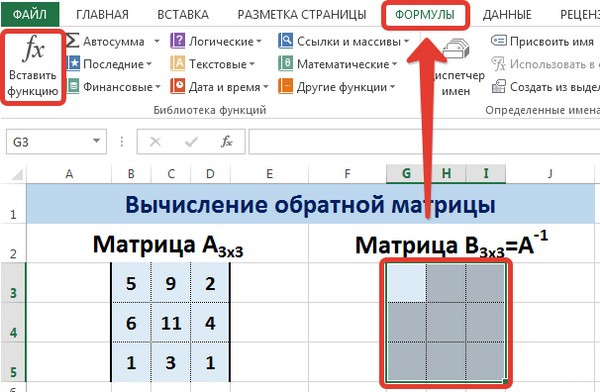
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.

В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения

Мы получили обратную матрицу.

Видео:Собственные векторы и собственные значения матрицыСкачать

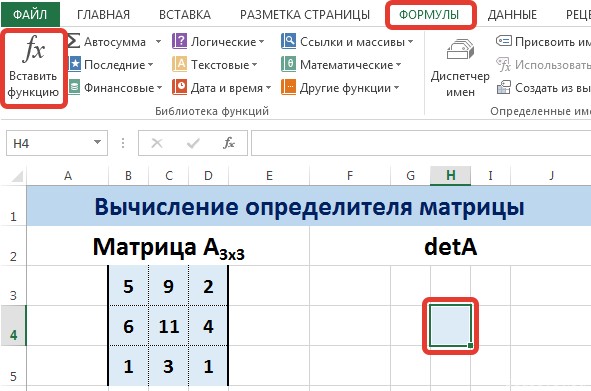
Нахождение определителя матрицы в Excel

Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.

Как найти определить матрицы в Excel

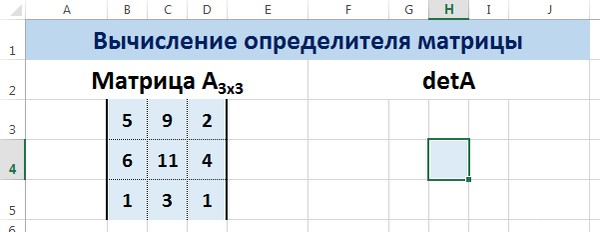
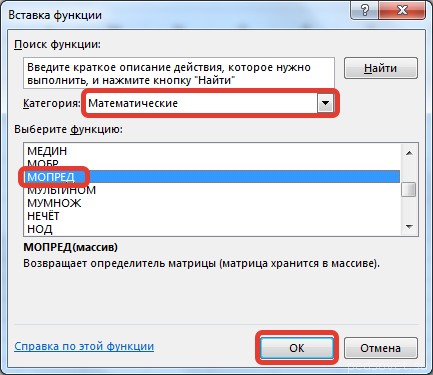
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().

Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.

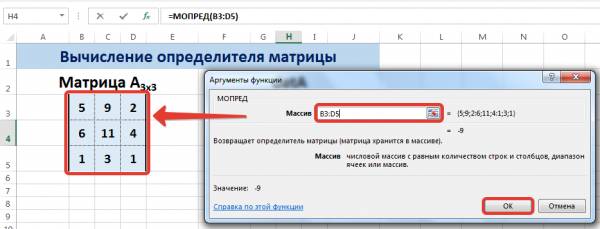
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

Нажмите для увеличения

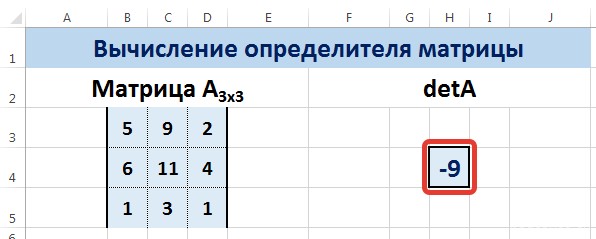
Мы вычислили определитель матрицы А.

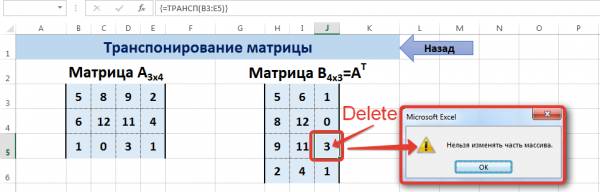
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения

Мы можем удалить только все элементы этой матрицы.

Видео:Простой Excel. Транспонирование матриц.Скачать

Видеоурок

Кратко об авторе:

Шамарина Татьяна Николаевна — учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Видео:Как найти определитель матрицы в EXCELСкачать

Векторы и матрицы в Excel

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:Простой Excel. Определитель матрицы.Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Векторы и матрицы в Excel

C овокупность n чисел , заданных в определенном по­рядке, называется n -мерным вектором. Числа a _i – компонент s или координат s вектора, n —размерностью вектора.

Два n -мерных вектора и называются равными, если все их соответствующие компоненты равны: .

Суммой двух n -мерных векторов и называется n -мерный вектор

.

Операция сложения векторов обладает свойствами коммутативности и ассоциативности .

Вектор , все компоненты которого равны нулю, называется нуль-вектором. Нуль-вектор ведет себя при сложения векторов аналогично числу нуль в арифметике.

Вектор называется противоположным вектору . Очевидно,

Операция вычитания векторов определяется как сложение с противоположным вектором .

Под произведением вектора на число  понимают вектор .

Умножение вектора на число обладает свойством ассоциативности и свойством дистрибутивности относительно векторного и числового сомножителей .

Модуль (норма, длина) вектора .

Пример вычисления модуля вектора (2, 5, 3, -4) приведен на рисунке 1.

Р
исунок 1 – Вычисление длины вектора

Здесь применены функция = КОРЕНЬ ( число ), где аргументом функции может быть либо конкретное число, либо адрес ячейки, в которой оно записано, и функция = СУММКВ ( число1 ; число2 ;…), где аргументами функции являются адреса ячеек (адрес массива) с координатами вектора.

В общем случае скалярное произведение двух векторов , где — угол между векторами. Скалярным произведение двух n -мерных векторов и может быть определено как сумма произведений одноименных координат данных векторов:

.

Операция скалярного умножения векторов обладает следующими свойствами:

.

В Excel скалярное произведение векторов вычисляется с помощью функции = СУММПРОИЗВ ( массив1 ; массив2;… ), где массив1 ; массив2;…- от 2 до 30 массивов, чьи компонент нужно перемножить, а затем сложить полученные произведения. Все массивы должны иметь одну и то же размерность (пример на рисунке 2).

Векторным произведением вектора на вектор называется вектор , длина которого численно равна площади параллелограмма построенного на векторах и , перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от к вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора (рисунок 3).

Треугольник, стороны которого есть стороны параллелограмма и его диагонали имеет площадь, равную половине величины векторного произв
едения двух векторов.

Р
исунок 2 – Определение скалярного произведения двух векторов

Значение векторного произведения определяется следующим образом:

На рисунке 4 приведен пример вычисления векторного произведения векторов, площади параллелограмма, треугольника. Проверка правильности вычисления векторного произведения заключается в проверке соответствия нулю величины скалярных произведений векторов и

Р
исунок 4 – Вычисление векторного произведения векторов

Перейдем к рассмотрению основных операций матричного исчисления.

Числа, расположенные в виде прямоугольной таблицы, состоящей из m строк и n столбцов, образуют матрицу размера m х n :

Две матрицы A и B одного и того же размера m × n являются равными, если равны все их соответствующие элементы:

Матрица, состоящая из одного столбца (т. е. если n = 1) или из од- ной строки (т. е. если m = 1), называется вектором — столбцом или, соответственно, вектором — строкой.

Матрица называется нулевой, если все ее элементы равны нулю. Нулевая матрица обозначается

При n = m матрица называется квадратной, а число ее строк (столбцов) – порядком матрицы. Элементы квадратной матрицы образуют ее главную диагональ.

Квадратная матрица называется треугольной, если все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю:

Квадратная матрица называется единичной, если все элементы ее главной диагонали равны единице, а остальные — нулю:

Если в матрице А заменить строки столбцами, сохранив их порядок, то получится новая матрица

называемая транспонированной по отношению к матрице А.

Если А=А Т , то такая матрица называется симметричной.

В Excel для транспонирования матриц используется функция =ТРАНСП(массив) – рисунок 5.

Р
исунок 5 – Вызов функции ТРАНСП

Пример. Имеем исходную матрицу

.

Из определения ясно, что транспонированной будет матрица А Т :

.

Решение задачи в Excel представлено на рисунке 6

Рисунок 6 – Транспонирование матрицы

Порядок решения следующий:

— определить место для транспонированной матриц (в рассматриваемом примере это G2:I4);

— в ячейку размещения первого элемента транспонированной матрицы ввести формулу =ТРАНС(С2:E5);

— выделить массив ячеек, в которых будут размещаться все элементы транспонированной матрицы;

— нажать Shit + Ctrl + Enter .

Суммой матриц А и В одинакового размера является матрица С , элементы которой равны сумме соответствующих элементов суммируемых матриц:

Произведение матрицы на число  — то матрица, элементы которой получаются умножением всех элементов исходной матрицы на данное число:

Умножение матрицы на матрицу определяется только при условии, что число столбцов первого сомножителя А равно числу строк второго сомножителя В . Под произведением матрицы размером m x k на матрицу размером k x n понимают матрицу размером m x n , элемент которой равен скалярному произведению i -й строки матрицы на j -й столбец матрицы :

В Excel для вычисления произведения матриц используется функция

= МУМНОЖ ( массив1 ; массив2 ), где массивы – совокупности элементов перемножаемых матриц (рисунок 7).

Р
исунок 7 – Умножение матриц

Формула для расчета произведения матриц должна быть введена как формула массива!

Пусть даны матрицы

Вычислим их произведение в Excel (рисунок 8).

— шаг1 – определение области размещения результата (на рисунке 8 выделена пункитом);

— шаг 2 – ввод в начальную ячейку результирующего массива формулы умножения матриц;

—
шаг 3 – выделить результирующий массив и нажать F2;

—
шаг 3 – нажать Shift+Ctrl+Enter.

Рисунок 8 – Вычисление произведения матриц

Действие умножения матрицы на матрицу обладает свойствами:

Отметим, что в общем случае

Если условие равенства произведения матриц при изменении их последовательности выполняется, то матрицы называются перестановочными между собой.

При умножении квадратной матрицы саму на себя получаем квадратную матрицу второй степени, при n -кратном умножении получим квадратную матрицу n -го порядка ( n -й степени).

Определитель (или детерминант) матрицы – одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы, – определитель равен нулю.

Для матрицы первого порядка значение определителя равно единственному элементу этой матрицы.

Для матрицы 2х2 определитель вычисляется как

Для матриц более высоких порядков n x n определитель можно вычислить, применив следующую рекурсивную формулу:

, где – дополнительный минор к элементу .

Возможно разложение как по строкам, так и по столбцам.

В
Excel определитель вычисляется с помощью функции = МОПРЕД ( массив ), где массив есть совокупность элементов матрицы (рисунок 9).

Рисунок 9 – Расчет определителя матрицы

Квадратная матрица называется неособенной ( невырожденной ), если ее определитель не равен нулю. В противном случае она называется особенной ( вырожденной ) или сингулярной .

Детерминант треугольной матрицы равен произведению ее диагональных элементов

Обратной матрицей к матрице называют такую матрицу, для которой
А А -1 = E

Обратную матрицу можно найти по следующей формуле:

, где – определитель матрицы, – транспонированная матрица.

Н
а рисунке 10 приведен пример определения обратной матрицы с помощью функции Excel = МОБР ( массив ).

Рисунок 10 – Расчет обратной матрицы

Заметим, что функция применяется к массиву как в ранее приведенных примерах.

Проверим выполнение условия А А -1 = E (рисунок 11)

Р
исунок 11- Произведение матрицы на обратную матрицу

Собственным числом квадратной матрицы

называется такое число , которое обращает определитель матрицы в 0: .

Или, по-другому, собственными числами матрицы А являются корни уравнения и только они.

Матрица называется характеристической матрицей матрицы А , многочлен называется характеристическим многочленом матрицы А , уравнение называется характеристическим уравнением матрицы А.

Для вычисления собственных чисел существуют классические приемы, сводящиеся к решению полиномиальных уравнений. Собственные числа определяют системы компьютерной математики. Найдем все собственные числа произвольной квадратной матрицы с помощью Excel на примере квадратной матрицы размерностью 3х3:

Необходимо найти такие значения  , при котором

Оформим лист Excel следующим образом (рисунок 12):

Рисунок 12 – Вычисление собственного числа матрицы

В ячейку B2 введено =2-F2; в ячейку С3 — =-6-F2; в ячейку D4 — =1-F2.

Из рисунка 12 видно, что при  =0 определитель также равен 0, т.е.  =0 есть первое собственное число матрицы.

Д

ля определения других собственных числе воспользуемся поиском (Меню Сервис-Поск решения …) – рисунок 13, установив целевую ячейку $E$2, в которой вычисляется значение определителя матрицы. Требуемое значение определителя – 0. Поиск осуществляется путем подбора значения  , отображаемом в ячейке $F$2.

Рисунок 13 – Вычисление собственного числа матрицы

О щелчку на кнопке Выполнить, появляется окно Результат поиска решения (рисунок 14).

Рисунок 14 – Результат поиска решения

Выбираем Сохранить найденное решение и Тип отчета – Результаты . Щелкаем на Ок. Получаем ожидаемый результат  =0.

П
овторим выполненные действия, введя в окне Поиск решения ограничение $F$2>=1 (рисунок 15):

Рисунок 15 – Ввод ограничения

В результате поиска получаем второе значение собственного числа:  =3.

Повторим поиск при ограничении.

Если установить в ограничениях  >=4, то поиск не находит решения. Ищем отрицательное собственное число и устанавливаем в ограничениях 

П
ри добавлении в систему ограничений Е1>=-10 (рисунок 16) поиск нашел третье собственное число, равное -6 (рисунок 17)

Р
исунок 16 – Поиск собственного числа при двухстороннем ограничении

Рисунок 17 — Результат поиска третьего собственного числа

Собственным вектором соответствующим собственному числу λ называют такой вектор , который удовлетворяет матричному равенству:

Найдем собственный вектор матрицы

Данная матрица имеет собственные числа: λ1 = 0 λ2 = 3 λ3 = -6.

1. Заносим содержимое ячеек матрицы в ячейки таблицы (B2:D4).

2. В ячейку (B6) вводим λ для которого необходимо найти собственный вектор. Пусть λ = 3.

3. В ячейки (F2:F4) поместим любые числа: F2 = 1; F3 = 1; F4 = 1.

4. В ячейки (G2:G4) заносим произведение матрицы (ячейки В2:В4) на вектор (ячейки F2:F4).

5. В ячейки (H2:H4) заносим умножение столбца на собственное число λ находящийся в ячейки (B6).

6. В ячейки (I2:I4) заносим разность столбцов (F2:F4) и (H2:H4).

7. В главном меню открываем Сервис — Поиск решения . Вводим следующие данные: Целевая ячейка $I$2, Равной значению (0); Изменяя ячейки $F$2:$F$4; Ограничения $I$3=0; $I$4=0.

Нажать кнопку « Выполнить ».

В
ячейках (F2:F4) появятся числа, эти это и есть собственный вектор для данного собственного числа (рисунок 18).

Рисунок 18 – Определение собственного вектора матрицы

Последовательно выполнить операции п.п. 2, 3, 7 при остальных значениях собственных чисел матрицы.

Задания для самостоятельной работы

Повторить решение всех примеров, приведенных в Лекции №5.

Сформировать случайным образом два вектора, состоящих из 5 элементов. Элементы векторов должны быть в диапазоне -5…+15

Определить длину векторов.

Вычислить сумму и разность векторов.

Определить скалярное произведение этих векторов.

Определить угол между векторами.

Определить векторное произведение двух векторов.

Проверить правильность вычисления векторного произведения путем определения скалярного произведения каждого из исходных векторов с результатом вычисления векторного произведения.

Сформировать случайным образом матрицу размером 4х4 и матрицу 4х3. Элементы матрицы должны быть в диапазоне -10…+20.

Получить транспонированные матрицы исходных матриц.

Проверить правильность решения путем умножения исходной матрицы на транспонированную.

Определить произведение исходных матриц.

Найти матрицу 3-го порядка для исходной квадратной матрицы.

Определить детерминант исходной квадратной матрицы.

Видео:Простой Excel. Нахождение обратной матрицы.Скачать

Операции с матрицами в Excel

Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.

Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.

Видео:Простой Excel. Умножение матриц.Скачать

Формулы массива

В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:

1. Выделить набор ячеек, где будут выводиться значения.
2. Непосредственно введение формулы.
3. Нажатие последовательности клавиш Ctrl + Shift + Ввод.

После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.

Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.

Видео:А.7.35 Собственные вектора и собственные значения матрицыСкачать

Что можно делать с матрицами

В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.

Транспонирование

Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.

Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.

Далее есть несколько методов, как можно осуществить транспонирование.

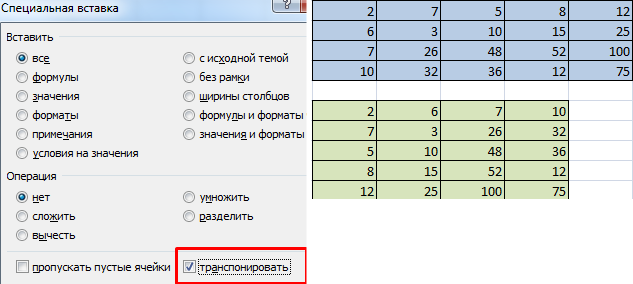
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».

Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.

Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП . Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.

После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:

1. Выделить набор ячеек, отведенных под транспонированную матрицу.
2. Нажать клавишу F2.
3. Нажать на горячие клавиши Ctrl + Shift + Enter.

Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.

Видео:как ... перемножить две матрицы в ExcelСкачать

Сложение

Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.

В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.

=Первый элемент первой матрицы + Первый элемент второй матрицы

Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.

Видео:Матрицы и векторыСкачать

Умножение

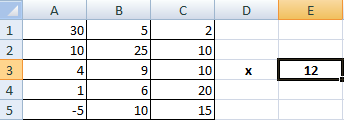
Предположим, у нас есть такая таблица, которую следует умножить на 12.

Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.

При этом важно указывать абсолютные ссылки на ячейки.

Итого, получится такая формула.

=A1*$E$3

Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.

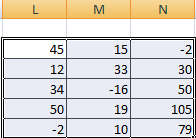
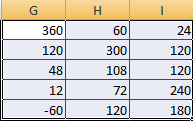
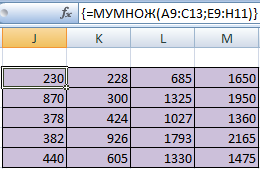
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.

Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:H11). Не стоит забыть нажать Ctrl + Shift + Enter.

Видео:Собственные значения матрицыСкачать

Обратная матрица

Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР .

Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4) . В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.

Видео:Собственные векторы и собственные числа линейного оператораСкачать

Поиск определителя матрицы

Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД .

Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)

Видео:Собственные значения и собственные векторы. ТемаСкачать

Несколько примеров

Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.

Умножение и деление

Метод 1

Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.

Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке H4. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.

Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.

Не стоит забывать о том, ячейку H4, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.

Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.

Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.

Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.

Метод 2

Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.

Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.

Деление осуществляется аналогичным образом, только знак * нужно заменить на /.

Сложение и вычитание

Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.

Метод 1

Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.

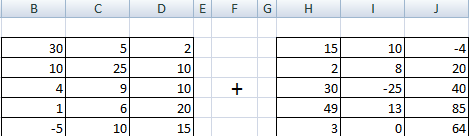
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:

Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.

Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.

Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.

Метод 2

Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.

Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.

Пример транспонирования матрицы

Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП() .

Выделяем диапазон для ячеек матрицы АТ.

Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП . После этого свои действия подтверждаются кнопкой ОК.

Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».

Важно . Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.

В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.

Поиск обратной матрицы

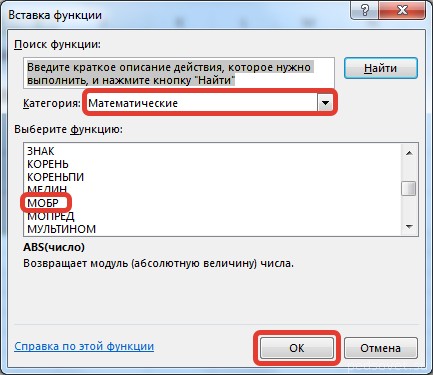
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР() .

Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».

Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР . После того, как мы ее выберем, нужно нажать на клавишу ОК . Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.

Видео:7 4 Собственные векторы и собственные значенияСкачать

Выводы

Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.

📽️ Видео

А.7.40 Метод Якоби поиска собственных векторов и значений симметричных матрицСкачать

17 Функции Excel НАЙТИ и ПОИСКСкачать