Решение линейного алгоритма окружности (8 видео)

Решение линейного алгоритма окружности

Исполнитель Черепаха может ходить по полю и рисовать линии пером. Если перо поднято, она просто перемещается в другое место, если перо опущено – рисует за собой линию.

Среда Черепахи – плоскость с системой координат. В начале работы с программой Черепаха находится в начале координат. Черепаха подчиняется командам, входящим в ее Список Команд Исполнителя, и может нарисовать любой рисунок. Размеры поля Черепахи и смещение начала координат можно задать в специальном окне настройки.

Чтобы вручную очистить рабочее поле Черепахи, надо нажать клавишу F12.

Содержание

Как управлять Черепахой. Решение линейных алгоритмов
Заливка замкнутой области
Окружности
Практические задания
Решение линейного алгоритма окружности
«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС» методическая разработка по информатике и икт (9 класс) на тему
Скачать:
Предварительный просмотр:
Введение
Основная часть
Задания, которые рассматриваются на занятии:
Проверяемые элементы содержания
Основное содержание теоретической части
Задания на этапе первичного закрепления
📸 Видео

Как управлять Черепахой. Решение линейных алгоритмов

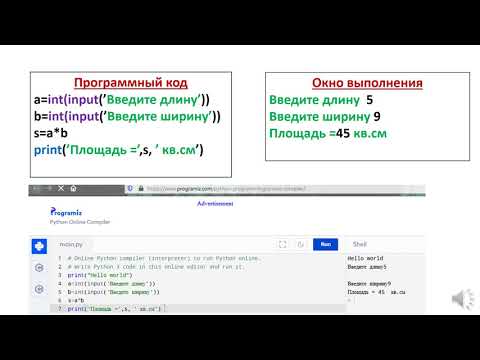
Задача 1. Составить программу для рисования квадрата со стороной 40 шагов.

Как вы знаете, все углы квадрата равны 90 градусов, поэтому программа выглядит так:

Квадрат /*название программы*/

покажись; /*черепашка появляется на поле*/
опусти_перо; /*при движении черепашка будет оставлять линию*/
вперед ( 40 ); /*черепашка движется вперед на 40 шагов*/
вправо ( 90 ); /*черепашка поворачивается вправо на 90 градусов*/
вперед ( 40 );
вправо ( 90 );
вперед ( 40 );
вправо ( 90 );
вперед ( 40 );

> /*конец программы*/

Заливка замкнутой области

Черепаха умеет также раскрашивать рисунки, заливая замкнутую область заданным цветом.

При этом необходимо выполнение следующих условий:

Область должна быть замкнуты, то есть в границе не может быть разрывов, иначе краска «вытекает».
В момент заливки черепаха должна находится внутри этой области.
Черепаха не должна находиться в точке, которая имеет тот же цвет, что и граница.

Задача 2. Составить программу для рисования желтого квадрата со стороной 40 шагов и с границей синего цвета.

Квадрат

покажись;
опусти_перо;
цвет ( СИНИЙ ); /*цвет пера черепашки меняется на синий */
вперед ( 40 );
вправо ( 90 );
вперед ( 40 );
вправо ( 90 );
вперед ( 40 );
вправо ( 90 );
вперед ( 40 );
вправо ( 135 );
вперед ( 5 );
залить ( ЖЕЛТЫЙ ); /*черепашка заливает замкнутую область желтым цветом*/

Учтите, что если вы не использовали команду цвет, все линии рисуются черным цветом. Чтобы в самом начале залить экран каким-нибудь фоном, надо также использовать команду залить.

Окружности

Черепаха умеет сама рисовать окружности, для этого надо перевести ее в центр окружности и применить специальную команду.

Для рисования окружности, центр которой находится в том месте, где стоит Черепаха, используют команду
окружность ( R );
где R — радиус окружности

Цвет окружности определяется установленным цветом линий (то есть последней командой цвет). Учтите, что Черепаха рисует окружность только тогда, когда ее перо опущено.

Практические задания

Использован материал из книги «Алгоритмы и исполнители», автор Поляков К.

Видео:Программирование линейных алгоритмов | Информатика 8 класс #23 | ИнфоурокСкачать

Решение линейного алгоритма окружности

На практике линейные алгоритмы в чистом виде встречаются редко: при расчете арифметических и алгебраических выражений, при расчете по формулам, при решении ряда бытовых задач.

В фигурных скобках записаны пояснения (комментарии) к операторам для удобства работы пользователям с данной программой, но компьютер комментарии не читает.

Рассмотрим задачу 1.

Найдите сумму и произведение трех введенных с клавиатуры чисел.

Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.

Входные данные: 1 2 3. Выходные данные: S=6, P=6.

Program zadacha1;
Var
a,b,c,S,P: integer;
Begin
writeln (‘Введите три числа’);
readln (a,b,c);
S:=a+b+c;
P:=a*b*c;
writeln (‘S=’, S);
writeln (‘P=’, P);
readln;
End.

Даны длины двух катетов прямоугольного треугольника. Определить периметр этого треугольника.

Входные данные: 3 4

Выходные данные: P=12

Program zadacha2;
Var a,b,P: real;
Begin
writeln (‘Введите два катета’);
readln (a,b);
P:=a+b+sqrt(sqr(a)+sqr(b));
readln;
End.

ЗАДАЧА 3:
Вычислить длину окружности и площадь круга. Радиус вводится с клавиатуры.

program zadacha3 ;

const Pi = 3.14159;

write (‘ введите радиус ‘);

writeln (‘Длина окружности’, L );

writeln (‘ Площадь круга ‘, S);

ЗАДАЧА 4:

Пешеход шел по пересеченной местности. Его скорость движения по равнине v1 км/ч, в гору — v2 км/ч и под гору — v3 км/ч. Время движения соответственно t1, t2 и t3 ч. Какой путь прошел пешеход?

Видео:Линейные алгоритмыСкачать

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»
методическая разработка по информатике и икт (9 класс) на тему

Занятие, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Практическая работа на тему

«Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг» с учетом требований ФГОС»

В данной разработке представлены задачи с геометрическим содержанием по теме «Окружность и круг» для 9 класса. Для этих задач разработаны алгоритмы и программы на псевдокоде и языке Паскаль. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе.

Видео:ВСЯ СЛОЖНОСТЬ АЛГОРИТМОВ ЗА 11 МИНУТ | ОСНОВЫ ПРОГРАММИРОВАНИЯСкачать

Скачать:

Вложение	Размер
prakticheskoe_zanyatie_algoritmy_geom_zadachi_shirobokovagi.docx	566.42 КБ

Видео:Математика это не ИсламСкачать

Предварительный просмотр:

учитель математики информатики

Видео:Информатика, 6 кл Программирование линейных алгоритмовСкачать

Введение

Одна из главная задач ФГОС, которые призваны реализовать развивающий потенциал общего среднего образования — готовить своих учеников к жизни, обеспечить ребенку общекультурное, личностное и познавательное развитие, вооружить умением учиться. Перед выпускниками, вступающими в самостоятельную жизнь, встаёт проблема решать новые, неизвестные задачи, которые неизбежно встанут перед ними. Результат образования можно «измерить» умением успешно решать такие задачи.

В новых стандартах метапредметным результатам уделено особое внимание, поскольку именно они обеспечивают более качественную подготовку учащихся к самостоятельному решению проблем, с которыми встречается каждый человек на разных этапах своего жизненного пути в условиях быстро меняющегося общества. Предмет информатики и ИКТ можно рассматривать как метапредмет, позволяющий более глубоко развивать межпредметные связи учебных дисциплин в средней общеобразовательной школе. Программирование обучает методам мышления, общим подходам к постановке и решению задач. Поэтому выбрана тема занятия, на котором решаются геометрические задачи с использованием алгоритмики и программирования.

Видео:04. Линейный алгоритмСкачать

Основная часть

Тема занятия : Разработка алгоритмов и программ для решения задач с геометрическим содержанием по теме «Окружность и круг».

Видео:Python. Программирование линейных алгоритмовСкачать

Задания, которые рассматриваются на занятии:

вычисление длины окружности по заданному радиусу;
нахождение площади круга, ограниченного окружностью заданного радиуса;
нахождение площади кольца по внутреннему и внешнему радиусам;
вычисление расстояния между двумя точками с заданными координатами;
найти площади сектора по радиусу и дуге;
определение минимального радиуса круга, в который попадают точки, заданные координатами на плоскости;

Для решения задач используем линейные структуры, ветвления и циклы.

Видео:C++ | Линейный алгоритм в С++ (А + В)Скачать

Проверяемые элементы содержания

Формальное исполнение алгоритма, записанного на естественном языке или умение создавать линейный алгоритм для формального исполнителя с ограниченным набором команд.

Знание основных конструкций языка программирования, понятия переменной, оператора присваивания.

Умение исполнить алгоритм для конкретного исполнителя с фиксированным набором команд.

Анализ алгоритма, содержащего вспомогательные алгоритмы, цикл и ветвление.

Умение анализировать результат исполнения алгоритма.

Видео:ИНФОРМАТИКА 8 класс. Линейные алгоритмы на языке Паскаль | ВидеоурокСкачать

Основное содержание теоретической части

Алгоритмы работы с величинами: константы, переменные, понятие типов данных, ввод и вывод данных.

Структура программы на языке Паскаль. Представление данных в программе. Правила записи основных операторов: присваивания, ввода, вывода, ветвления, циклов.

Этапы решения задачи с использованием программирования: постановка задачи, формализация, алгоритмизация, кодирование, отладка, тестирование.

Практика на компьютере: знакомство с системой программирования на языке Паскаль; ввод, трансляция и исполнение данной программы; разработка и исполнение линейных, ветвящихся и циклических программ.

Переменная, константа, операторы ввода/вывода, оператор присваивания, арифметические операции с переменными.

Создание с использованием свойств геометрических фигур математических моделей для решения задач практического характера и задач из смежных дисциплин (для данного занятия – конкретно геометрии), исследовать полученные модели и интерпретировать результат.

Задачи на применение линейных алгоритмических структур. В ходе решения задач повторяются формулы курса геометрии 9 класса: вычисление длины окружности, площади круга, площади кольца, площади сектора, расстояния между двумя точками на плоскости, заданных координатами (метод координат в курсе геометрии).

Видео:Блок-схемы для начинающих (Блок схемы алгоритмов)Скачать

Задания на этапе первичного закрепления

Рассмотрим подробно задачи геометрического содержания с постановкой, математической моделью, алгоритмом, программой на языке Паскаль и полученными результатами (скриншот).

Задача 1. Вычислить длину окружности по заданному радиусу.

Результат – найти длину окружности.
Исходные данные – радиус окружности.
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительное число.

Математическая модель. Вычислить длину окружности по формуле

Описать переменные. Ввести данные.

Вычислить по формуле длины окружности C= 2*π*R.

Write( ‘Введите радиус окружности R= ‘ );

WriteLn( ‘Длина окружности С= ‘ ,C: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 37, 57344814. Верно.

Задача 2. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

Результат – площадь круга.
Исходные данные – длина окружности.
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительное число.

Математическая модель. Выразить радиус R из формулы длины окружности C= 2*π*R. Вычислить радиус R=C/(2* π). Вычислить площадь круга по формуле S= .

Описать переменные. Ввести данные.

Выразить радиус R из формулы длины окружности.

Вычислить радиус по формуле R=C/(2* π). Вычислить площадь круга по формуле S= .

Write( ‘Введите длину окружности С= ‘ );

WriteLn( ‘Площадь круга = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверка результата с помощью калькулятора, получим число 426, 5116724. Значит, программа правильна.

Задача 3. Найти площадь кольца, внутренний радиус которого равен r, а внешний – заданному числу R (R> r).

Результат – найти площадь кольца.
Исходные данные – внутренний радиус равен r, а внешний – R (R> r).
Ограничения на результат – положительное число.
Ограничения на исходные данные – положительные числа.

Математическая модель. Найдём площадь кольца по формуле S к =π*(R*R-r*r), где – R — внешний радиус, r-внутренний радиуc, (R> r).

Описать переменные. Ввести данные.

Вычислить по формуле площадь кольца по формуле S к =π*(R*R-r*r).

Writeln( ‘Введите радиусы окружностей R2 и R1 ‘ );

S := pi * (R2 * R2 — R1 * R1);

WriteLn( ‘Площадь кольца S = ‘ , S: 5 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 12, 56637061. Верно.

Задача 4. Вычислить расстояние между двумя точками с координатами X1, Y1 и X2, Y2.

Результат – найти расстояние R между двумя точками на плоскости.
Исходные данные – даны координаты точек (X1, Y1) и (X2, Y2).
Ограничения на результат – ограничение на расстояние R>=0
Ограничения на исходные данные — ограничений на координаты нет.

Математическая модель. Выведем формулу для вычисления расстояния между двумя точками на плоскости.

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x b — x a ;
BC = y b — y a .

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости: AB = .

Описать переменные. Ввести данные.

Вычислить расстояние между точками по формуле R= .

Напишем алгоритм на псевдокоде

* вывод (‘Введите координаты (x и y) точки 1’)

* вывод (‘Введите координаты (x и y) точки 2’)

* R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

* вывод (‘расстояние между точками 1 и 2 равно ‘, R:10:3);

X1, X2, Y1, Y2, R: Real ;

Writeln( ‘Введите координаты (x и y) точки 1’ );

Writeln( ‘Введите координаты (x и y) точки 2’ );

R := Sqrt(Sqr(X2 — X1) + Sqr(Y2 — Y1));

Write( ‘расстояние между точками 1 и 2 равно ‘ , R: 10 : 3 );

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора, получим число 4. Верно.

Задача 5. Найти площадь сектора, радиус которого равен 15.4, а дуга содержит заданное число радиан ϕ .

Результат – площадь сектора.
Исходные данные – величина угла в радианах.
Ограничения на результат – положительное число.
Ограничения на исходные данные – значение дуги в радианах меньше, чем 2π ≈ 6.28. Иначе сектор будет по величине больше круга.

Модель. Выведем формулу для вычисления площади сектора через угол, выраженный в радианах. Сектор круга ограничивается дугой между двумя точками А и В на окружности и двумя радиусами, проведёнными из концов дуги (точек А и В) к центру круга.

Два радиуса делят всю площадь круга на 2 сектора. Если угол между этими радиусами будет развёрнутым (180 0 ), то эти секторы будут между собой равны. Площадь сектора круга – это часть площади всей плоской фигуры, ограниченной окружностью с радиусом r. Площадь круга равна произведению квадрата радиуса на число S= . Площадь кругового сектора в радиан (полукруга) равна . Поэтому площадь сектора в один радиан в π раз меньше, т.е. равна : π. Значит, площадь сектора в α радиан равна =

* вывод (‘Введите величину дуги кругового сектора (в радианах)’)

* вывод (‘Площадь кругового сектора =’, S:8:2)

write(‘Введите величину дуги кругового сектора (в радианах) ‘);

writeln(‘Площадь кругового сектора = ‘, S:8:2)

Скриншот программы с результатами решения

Вывод. Программа работоспособна. Проверим результат с помощью калькулятора.

Задача 6. Даны координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn,yn). Определить минимальный радиус круга, в который попадают все эти точки. Центр круга находится в начале координат.

Результат – определить минимальный радиус круга, в который попадают точки с заданными координатами.
Исходные данные – координаты N точек на плоскости (x1,y1), (x2,y2), (x3,y3), . (xn, yn).
Ограничения на результат – неотрицательное действительное число.
Ограничения на исходные данные – координаты точек выражаются действительными числами, количество точек N — натуральное число.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И МЕТОД: Радиус круга с центром в начале координат вычисляется по формуле R= . Для наглядности рисунок.

АЛГОРИТМ. Вычисляем радиус (расстояние от начала координат до точки) для каждой точки, выбираем минимальное значение. Сравниваем два числа, наименьшее значение записываем как минимум. Это и будет минимальным значением радиуса. Так как количество точек известно, организуем цикл с параметром.